這次的課程筆記和上次隔了好久，因為為了搞懂 SVM 花了不少時間。和之前 神經網路 課程一樣，Ng 在 Coursera 上講述的內容非常有限，要搞懂 SVM 你只能尋求於其他方面的資料。經過對網上一些內容的對比後發現斯坦福的 CS229 講義寫得非常清晰。CS229 是 Andrew Ng 在斯坦福大學開設的機器學習課程，Coursera 上的課程可以說是 CS229 的簡化版本，而且整個課程的內容還在不斷更新，有興趣的同學可以把它作為更進一步的參考資料。（ 我已經將講義和 SMO 演算法的論文與程式碼放在一起了方便大家下載 ）

這次的課程筆記會闡述 SVM 的主要思路，從 最大間距分類器

開始，然後通過 拉格朗日對偶 得到原問題的 對偶 問題，使得我們可以應用 核技巧（ kernel trick ），用高效的方式解決高維問題。

點選 課程視訊 你就能不間斷地學習 Ng 的課程，關於課程作業的 Python 程式碼已經放到了 Github 上，點選 課程程式碼 就能去 Github 檢視（ 無法訪問 Github 的話可以點選 Coding 檢視 ），程式碼中的錯誤和改進歡迎大家指出。

以下是 Ng 機器學習課程第六週的筆記。

最大間距分類器

考慮 邏輯迴歸 的 預測函式 hθ(x)=g(θTx)$h_{\theta }(x)=g({\theta }^{T}x)$。當 θTx≫0${\theta }^{T}x\gg 0$ 或 θTx≪0${\theta }^{T}x\ll 0$ 時，就能十分確信 預測函式

的分類，因為 hθ(x)$h_{\theta }(x)$ 接近於 1 和 0。直觀的表達就是樣本越是遠離 決策邊界，就越確信它的分類。所以自然想到如果在多個 決策邊界 之間選擇，我們會選擇離所有樣本都比較遠的那個（ 考慮線性的情況 ）。

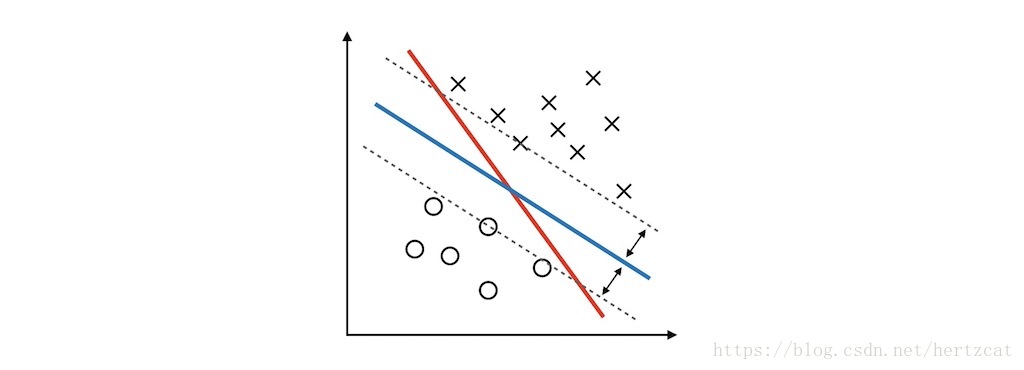
為了得到這樣的決策邊界，我們首先來看看如何用數學方式表達這個問題。通過一些簡單的 計算幾何 知識可以計算出每個樣本到 決策邊界 的距離（ geometric margin ），γ(i)${\gamma }^{(i)}$。為了方便之後的推導，還需要定義一個 functional margin，γ̂ (i)${\hat{\gamma }}^{(i)}$。

γ̂ (i)=y(i)(wTx(i)+b)γ(i)=y(i)((w||w||)Tx(

i)+b||w||)$${\hat{\gamma }}^{(i)}=y^{(i)}\left(w^T{x}^{(i)}+b\right){\gamma }^{(i)}=y^{(i)}\left({\left(\frac{w}{||w||}\right)}^T{x}^{(i)}+\frac{b}{||w||}\right)$$
在接下來的 SVM 討論中 y(i)$y^{(i)}$ 的取值為 {1,−1}$\{1,-1\}$（ 表示在決策邊界的哪一側，並使得距離的計算都是正的 ），當 wTx+b≥0$w^{T}x+b\ge 0$ 時取 1$1$，wTx+b<0$w^{T}x+b<0$ 時取 −1$-1$。還需要定義 γ̂ $\hat{\gamma }$ 為所有 γ̂ (i)${\hat{\gamma }}^{(i)}$ 中最小的值，γ$\gamma$ 為所有 γ(i)${\gamma }^{(i)}$ 中最小的值。於是要求離所有樣本都比較遠的決策邊界問題就成為了在給定約束條件下求最值的問題。
maxγ,w,bs.t.γy(i)(wTx(i)+b)≥γ,||w||=1.i=1,...,m$$\begin{array}{rl}ma{x}_{\gamma ,w,b}& \gamma \\ s.t.& y^{(i)}(w^T{x}^{(i)}+b)\ge \gamma ,& i=1,...,m\\ ||w||=1.\end{array}$$
然而上面的問題還不是一個直接可解的 優化問題，需要對它進行轉化（ 思路是把它轉化為標準的 凸優化問題 ）。首先我們用 functional margin 來替換 geometric margin，原問題變為：