識別MNIST資料集之(二):用Python實現神經網路
在這篇文章當中,我們將會用根據MNIST的資料集,跟大家介紹神經網路進行分類的基本原理和方法。
1.神經網路的正向計算
如果我們把神經網路當作一個黑盒來看,它的結構大概是這樣的:
輸入(層):一張圖片
計算過程 : 神經網路
輸出 (層): 這張圖片屬於每種分類的概率(或者說是分數)
現在我們來解釋一下
輸入是一張圖片,也就是這張圖片的各個畫素的值,向量化了之後的向量,對於MNIST來說,就是一個( 1, 28*28 )的向量。通過訓練,我們要讓這個神經網路自己提取這些畫素值的某種特徵,這樣當出現一個從來沒有見過的影象的時候,也能根據識別的特徵進行分類
計算過程:
眾所周知,神經單元的基本結構是這樣的
表示成向量,就是這樣的
W1 = [ w1, w2, w3 ]
假設我們輸入的圖片向量是I = [ i1, i2, i3 ]
那我們計算出的分數其實是 S = W1 * I = w1 * i1 + w2 * i2 + w3 * i3
但是這樣的表現力是不夠的,還需要加入偏移量 B1 = [ b1, b2, b3 ]
所以我們計算出的分數其實就是S = W1 * I + B1
雖然這是最最簡化的版本,但是基本的東西就是這樣,很簡單
根據現在的這個結構,我們只能算出一個分數,但是我們要對一個輸入的影象算出多個分數,才知道該把它分成那一類,我麼你現在要對權值矩陣做一定的調整
原來我們的權值是
W1 = [ w1, w2, w3 ]
現在我們的權值調整為
輸入仍然是
在運算之後我們得到一個分數的向量
這三個值分別就是我們得到的三個分類初步的分數,但是如果要進一步計算概率的話,就要計算它們的Softmax值,詳細的計算請見我的另外一篇文章,這裡理解成計算成各自的概率就可以了
在實際上計算的過程中,我們每次只處理一張圖片太慢了,所以一般是對一個batch的圖片一起進行計算,其實道理也是一樣的,只不過是輸入的矩陣從[ 1 * N ] 變成了 [ M * N ]而已
接下來我們要引入隱層的概念
我們上面的示例當中,儲存資料的節點,就只有一個輸入層,一個輸出層,這樣我們只能有一層的抽象,表現能力其實是不夠的,我們需要加入更多的節點,也就是隱層
我們其實可以把隱層理解成輸入向量的進一步抽象,在一步一步的抽象後,就可以得到每個分類的概率了
而隱層的結構和輸入層也是類似的,只不過在每次計算的過程中進行抽象,所以節點的數量也變少了
神經元以及代表的意義
矩陣運算的意義
非線性單元
這是神經網路中非常重要的一部分,雖然結構簡單,實現簡單,但是非常的重要,不可或缺
2.Softmax計算
當我們通過神經網路的計算過程計算出當前的特徵向量(就是圖片)屬於每個類別的分數的時候,我們需要將這個分數轉化為這個特徵向量屬於每個類別的概率,這個概率的計算就是通過Softmax來實現的
3.梯度下降
這是神經網路演算法中非常重要的部分,我們通過Softmax計算出了當前向量屬於每個類別的概率,而且通過標註的資料我們知道當前向量正確的分類。這樣我們就可以通過損失函式來調整各個權重,優化網路
比如我們通過計算得到
我們就可以對網路的權值進行優化
如果我們把梯度下降比作一個下山的過程的話,計算梯度就是計算在當前位置向哪個方向爬山最陡峭,然後朝著它的反方向朝著山下邁一步。當然顯而易見的是這種優化方法非常容易走到區域性極值點,所以有很多方法來優化,我們會在其他文章中詳細討論。
4.反向傳播
backpropagation,這是整個神經網路最難理解的地方(其實也沒那麼難),當我們計算出了Loss,進而算出了Loss對Wn的偏導的時候,我們也想知道,Loss對Wn-1的偏導,這樣我們才能對前面的權值網路做一些調整
而且還有一個反向傳播的好處就是,每個偏導計算一次就行了,雖然資料量也不是特別大,但是這多多少少提高了效率
我們通過正向的計算算出了score,並且根據定義算出了Loss,所以我們可以計算出Loss對score的偏導
而且我們之前也說了,在正向傳播的時候我們的score是這樣計算的,假設我們只有一層網路
所以W1的偏導就是
這很顯然就是鏈式法則的應用,無他
在這裡我們需要特別強調ReLU函式的偏導,ReLU函式的表示式我們知道很簡單
這個一個分段函式,對於分段函式求導我們當然就要分段來看
加入ReLU之後,我們的表示式就類似於這樣
所以當出大於0的時候,表示式就是原來的
偏導也按原來的方法進行計算
當輸出小於0的時候,表示式就變成了
所以偏導也自然就是0
具體實現
Talk is cheap, Show me the code
在扯了那麼多之後,我們還是要回到程式碼上來,看看具體是怎麼實現的,我們才能對理論有更好的瞭解
先附上完整的程式碼
# -*- coding:utf-8
import numpy as np
import struct
import matplotlib.pyplot as plt
import random
import pickle
class Data:
def __init__(self):
self.K = 10
self.N = 60000
self.M = 10000
self.BATCHSIZE = 2000
self.reg_factor = 1e-3
self.stepsize = 1e-2
self.train_img_list = np.zeros((self.N, 28 * 28))
self.train_label_list = np.zeros((self.N, 1))
self.test_img_list = np.zeros((self.M, 28 * 28))
self.test_label_list = np.zeros((self.M, 1))
self.loss_list = []
self.init_network()
self.read_train_images( 'train-images-idx3-ubyte')
self.read_train_labels( 'train-labels-idx1-ubyte')
self.train_data = np.append( self.train_img_list, self.train_label_list, axis = 1 )
self.read_test_images('t10k-images-idx3-ubyte')
self.read_test_labels('t10k-labels-idx1-ubyte')
def predict(self):
hidden_layer1 = np.maximum(0, np.matmul(self.test_img_list, self.W1) + self.b1)
hidden_layer2 = np.maximum(0, np.matmul(hidden_layer1, self.W2) + self.b2)
scores = np.maximum(0, np.matmul(hidden_layer2, self.W3) + self.b3)
prediction = np.argmax( scores, axis = 1 )
prediction = np.reshape( prediction, ( 10000,1 ) )
print prediction.shape
print self.test_label_list.shape
accuracy = np.mean( prediction == self.test_label_list )
print 'The accuracy is: ',accuracy
return
def train(self):
for i in range( 10000 ):
np.random.shuffle( self.train_data )
img_list= self.train_data[:self.BATCHSIZE,:-1]
label_list = self.train_data[:self.BATCHSIZE, -1:]
print "Train Time: ",i
self.train_network( img_list, label_list )
def train_network(self, img_batch_list, label_batch_list):
# calculate softmax
train_example_num = img_batch_list.shape[0]
hidden_layer1 = np.maximum( 0, np.matmul( img_batch_list, self.W1 ) + self.b1 )
hidden_layer2 = np.maximum( 0, np.matmul( hidden_layer1, self.W2 ) + self.b2 )
scores = np.maximum( 0, np.matmul( hidden_layer2, self.W3 ) + self.b3 )
scores_e = np.exp( scores )
scores_e_sum = np.sum( scores_e, axis = 1, keepdims= True )
probs = scores_e / scores_e_sum
loss_list_tmp = np.zeros( (train_example_num, 1) )
for i in range( train_example_num ):
loss_list_tmp[ i ] = scores_e[ i ][ int(label_batch_list[ i ]) ] / scores_e_sum[ i ]
loss_list = -np.log( loss_list_tmp )
loss = np.mean( loss_list, axis=0 )[0] + \
0.5 * self.reg_factor * np.sum( self.W1 * self.W1 ) + \
0.5 * self.reg_factor * np.sum( self.W2 * self.W2 ) + \
0.5 * self.reg_factor * np.sum( self.W3 * self.W3 )
self.loss_list.append( loss )
print loss, " ", len(self.loss_list)
# backpropagation
dscore = np.zeros( (train_example_num, self.K) )
for i in range( train_example_num ):
dscore[ i ][ : ] = probs[ i ][ : ]
dscore[ i ][ int(label_batch_list[ i ]) ] -= 1
dscore /= train_example_num
dW3 = np.dot( hidden_layer2.T, dscore )
db3 = np.sum( dscore, axis = 0, keepdims= True )
dh2 = np.dot( dscore, self.W3.T )
dh2[ hidden_layer2 <= 0 ] = 0
dW2 = np.dot( hidden_layer1.T, dh2 )
db2 = np.sum( dh2, axis = 0, keepdims= True )
dh1 = np.dot( dh2, self.W2.T )
dh1[ hidden_layer1 <= 0 ] = 0
dW1 = np.dot( img_batch_list.T, dh1 )
db1 = np.sum( dh1, axis = 0, keepdims= True )
dW3 += self.reg_factor * self.W3
dW2 += self.reg_factor * self.W2
dW1 += self.reg_factor * self.W1
self.W3 += -self.stepsize * dW3
self.W2 += -self.stepsize * dW2
self.W1 += -self.stepsize * dW1
self.b3 += -self.stepsize * db3
self.b2 += -self.stepsize * db2
self.b1 += -self.stepsize * db1
return
def init_network(self):
self.W1 = 0.01 * np.random.randn( 28 * 28, 100 )
self.b1 = 0.01 * np.random.randn( 1, 100 )
self.W2 = 0.01 * np.random.randn( 100, 20 )
self.b2 = 0.01 * np.random.randn( 1, 20 )
self.W3 = 0.01 * np.random.randn( 20, self.K )
self.b3 = 0.01 * np.random.randn( 1, self.K )
def read_train_images(self,filename):
binfile = open(filename, 'rb')
buf = binfile.read()
index = 0
magic, self.train_img_num, self.numRows, self.numColums = struct.unpack_from('>IIII', buf, index)
print magic, ' ', self.train_img_num, ' ', self.numRows, ' ', self.numColums
index += struct.calcsize('>IIII')
for i in range(self.train_img_num):
im = struct.unpack_from('>784B', buf, index)
index += struct.calcsize('>784B')
im = np.array(im)
im = im.reshape(1, 28 * 28)
self.train_img_list[ i , : ] = im
# plt.imshow(im, cmap='binary') # 黑白顯示
# plt.show()
def read_train_labels(self,filename):
binfile = open(filename, 'rb')
index = 0
buf = binfile.read()
binfile.close()
magic, self.train_label_num = struct.unpack_from('>II', buf, index)
index += struct.calcsize('>II')
for i in range(self.train_label_num):
# for x in xrange(2000):
label_item = int(struct.unpack_from('>B', buf, index)[0])
self.train_label_list[ i , : ] = label_item
index += struct.calcsize('>B')
def read_test_images(self, filename):
binfile = open(filename, 'rb')
buf = binfile.read()
index = 0
magic, self.test_img_num, self.numRows, self.numColums = struct.unpack_from('>IIII', buf, index)
print magic, ' ', self.test_img_num, ' ', self.numRows, ' ', self.numColums
index += struct.calcsize('>IIII')
for i in range(self.test_img_num):
im = struct.unpack_from('>784B', buf, index)
index += struct.calcsize('>784B')
im = np.array(im)
im = im.reshape(1, 28 * 28)
self.test_img_list[i, :] = im
def read_test_labels(self,filename):
binfile = open(filename, 'rb')
index = 0
buf = binfile.read()
binfile.close()
magic, self.test_label_num = struct.unpack_from('>II', buf, index)
index += struct.calcsize('>II')
for i in range(self.test_label_num):
# for x in xrange(2000):
label_item = int(struct.unpack_from('>B', buf, index)[0])
self.test_label_list[i, :] = label_item
index += struct.calcsize('>B')
def main():
data = Data()
data.train()
data.predict()
pickle.dump( data.loss_list, open( "gradient_data", "w" ), False )
if __name__ == '__main__':
main()
可以看到,整個程式碼的流程是,先讀取資料,然後訓練資料,然後拿測試集來做預測
函式主要有這幾個
def init_network(self)這個函式當中主要來初始化,用numpy.random產生給定shape的矩陣,矩陣的值符合正態分佈
self.read_train_images()
self.read_train_labels()這兩個函式是用來讀圖片的資料和標籤的資料,在這篇文章中進行了詳細的介紹,有興趣的同學可以看一下
def train(self):這個函式中呼叫了訓練神經網路的函式,上面的程式碼中是呼叫了10000次訓練函式
def train_network(self, img_batch_list,label_batch_list)這個函式就是訓練的主要函式
在訓練的過程中也採用了隨機取樣batch訓練的方法,這樣可以在損失一定的訓練精度的情況下大大提高訓練的效率
def __init__(self)這個函式進行整個系統的初始化,設定hyperparameters,讀取檔案等等
我們可以看一下這個訓練過程中,損失函式的變化曲線
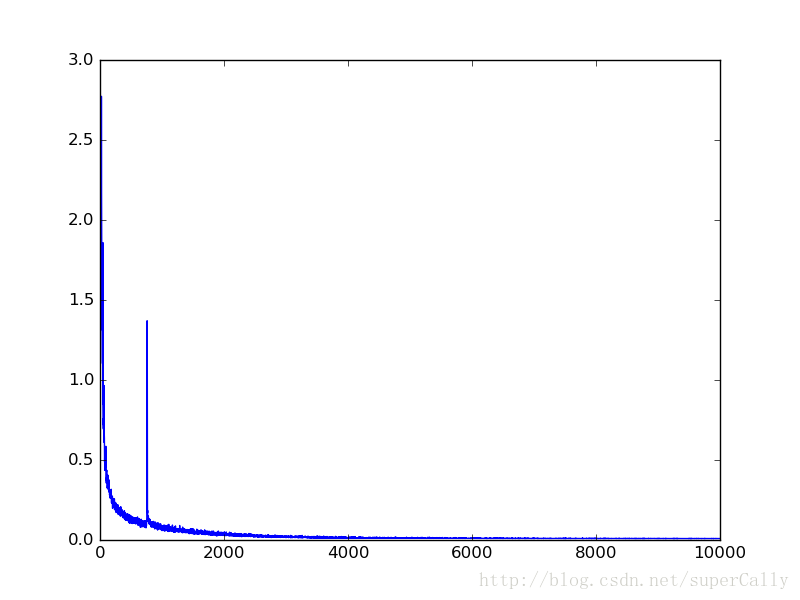
可以看到,中間幾次迭代的Loss發生了突變,但總體的效果還是很好的,最後的識別率達到了97%
