前言

在很早之前的紋理對映中，紋理存放的元素是畫素的顏色，通過紋理座標對映到目標畫素以獲取其顏色。但是我們的法向量依然只是定義在頂點上，對於三角形面內一點的法向量，也只是通過比較簡單的插值法計算出相應的法向量值。這對平整的表面比較有用，但無法表現出內部粗糙的表面。在這一章，你將瞭解如何獲取更高精度的法向量以描述一個粗糙平面。

DirectX11 With Windows SDK完整目錄

Github專案原始碼

法線貼圖

法線貼圖是指紋理中實際存放的元素通常是經過壓縮後的法向量，用於表現一個表面凹凸不平的特性，它是凹凸貼圖的一種實現方式。

開啟法線貼圖後的效果

關閉法線貼圖後的效果

法線貼圖中存放的法向量\((x, y, z)\)分別對應原來的\((r, g, b)\)。每個畫素都存放了對應的一個法向量，經過壓縮後使用24 bit即可表示。實際情況則是一張法線貼圖裡面的每個畫素使用了32 bit來表示，剩餘的8 bit(位於Alpha值)要麼可以不使用，要麼用來表示高度值或者鏡面係數。而未經壓縮的法線貼圖通常為每個畫素存放4個浮點數，即使用128 bit來表示。

下面展示了一張法線貼圖，每個畫素點位置存放了任意方向的法向量。可以看到這裡為法線貼圖建立了一個TBN座標系(左手座標系)，其中T軸(Tangent Axis)對應原來的x軸，B軸(Binormal Axis)對應原來的y軸，N軸(Normal Axis)對應原來的z軸。建立座標系的目的在後面再詳細描述。觀察這些法向量，它們都有一個共同的特點，就是都朝著N軸的正方向散射，這樣使得大多數法向量的z分量是最大的。

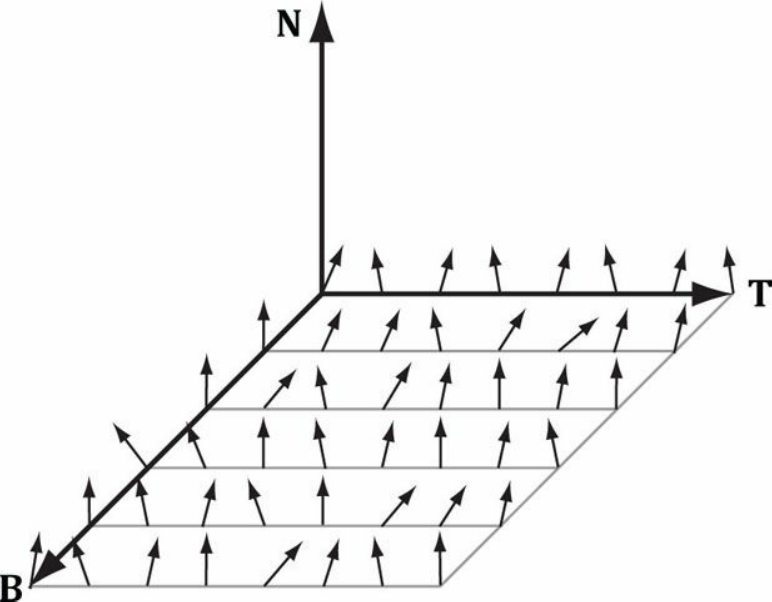
由於壓縮後的法線貼圖通常是以R8G8B8A8的格式儲存，我們也可以直接把它當做圖片來開啟觀察。

前面說到大部分法向量的z分量會比x, y分量大，導致整個圖看起來會偏藍。

法線貼圖的壓縮與解壓

經過初步壓縮後的法線貼圖的佔用空間為原來的1/4(不考慮檔案頭)，就算每個分量只有256種表示，也足夠表示出16777216種不同的法向量了。假如現在我們已經有未經過壓縮的法線貼圖，那要怎麼進行初步壓縮呢？

對於一個單位法向量來說，其任意一個分量的取值也無非就是落在[-1, 1]的區間上。現在我們要將其對映到[0, 255]的區間上，可以用下面的公式來進行壓縮：

\[f(x) = (0.5x + 0.5) * 255\]

而如果現在拿到的是24位法向量，要進行還原，則可以用下面的公式：

\[ f^-1(x) = \frac{2x}{255} - 1\]

當然，經過還原後的法向量是有部分的精度損失了，至少能夠映射回[-1, 1]的區間上。

通常情況下我們能拿到的都是經過壓縮後的法線貼圖，但是還原工作還是需要由自己來完成。

float3 normalT = gNormalMap.Sample(sam, pin.Tex);

經過上面的取樣後，normalT的每個分量會自動從[0, 255]對映到[0, 1]，但還不是最終[-1, 1]的區間。因此我們還需要完成下面這一步：

normalT = 2.0f * normalT - 1.0f;

這裡的1.0f會擴充套件成float3(1.0f, 1.0f, 1.0f)以完成減法運算。

注意：如果你想要使用壓縮紋理格式(對原來的R8G8B8A8進一步壓縮)來儲存法線貼圖，可以使用BC7(DXGI_FORMAT_BC7_UNORM)來獲得最佳效能。在DirectXTex中有大量從BC1到BC7的紋理壓縮/解壓函式。

紋理/切線空間

這裡開始就會產生一個疑問了，為什麼需要切線空間？

在只有2D的紋理座標系僅包含了U軸和V軸，但現在我們的紋理中存放的是法向量，這些法向量要怎麼變換到區域性物體上某一個三角形對應位置呢？這就需要我們對當前法向量做一次矩陣變換(平移和旋轉)，使它能夠來到區域性座標系下物體的某處表面。由於矩陣變換涉及到的是座標系變換，我們需要先在原來的2D紋理座標系加一條座標軸(N軸)，與T軸(原來的U軸)和B軸(原來的V軸)相互垂直，以此形成切線空間。

一開始法向量處在單位切線空間，而需要變換到目標3D三角形的位置也有一個對應的切線空間。對於一個立方體來說，一個面的兩個三角形可以共用一個切線空間。

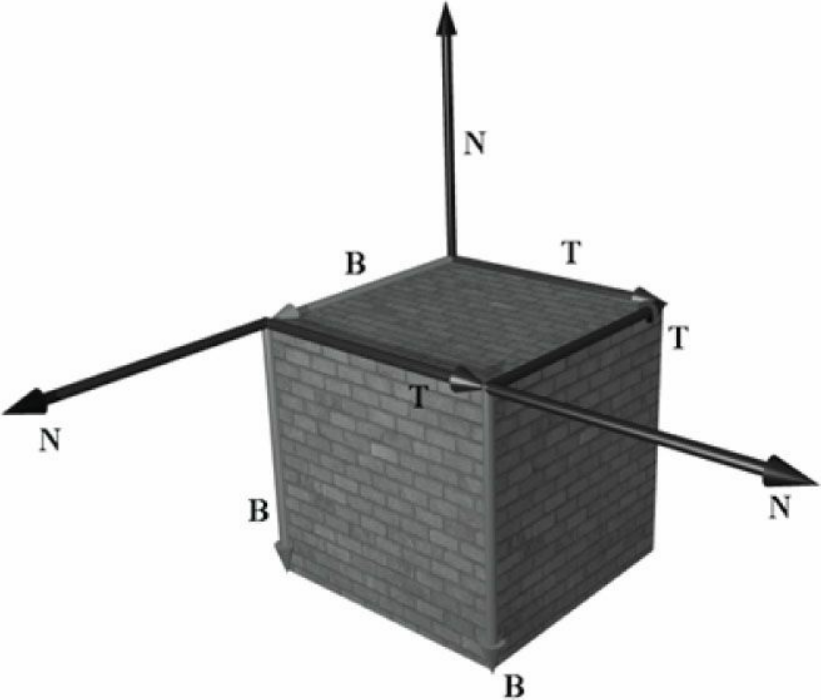
利用頂點位置和紋理座標求TBN座標系

現在假設我們的頂點只包含了位置和紋理座標這兩個資訊，有這樣一個三角形，它們的頂點為V0(x0, y0, z0), V1(x1, y1, z1), V2(x2, y2, z2)，紋理座標為(u0, v0), (u1, v1), (u2, v2)。

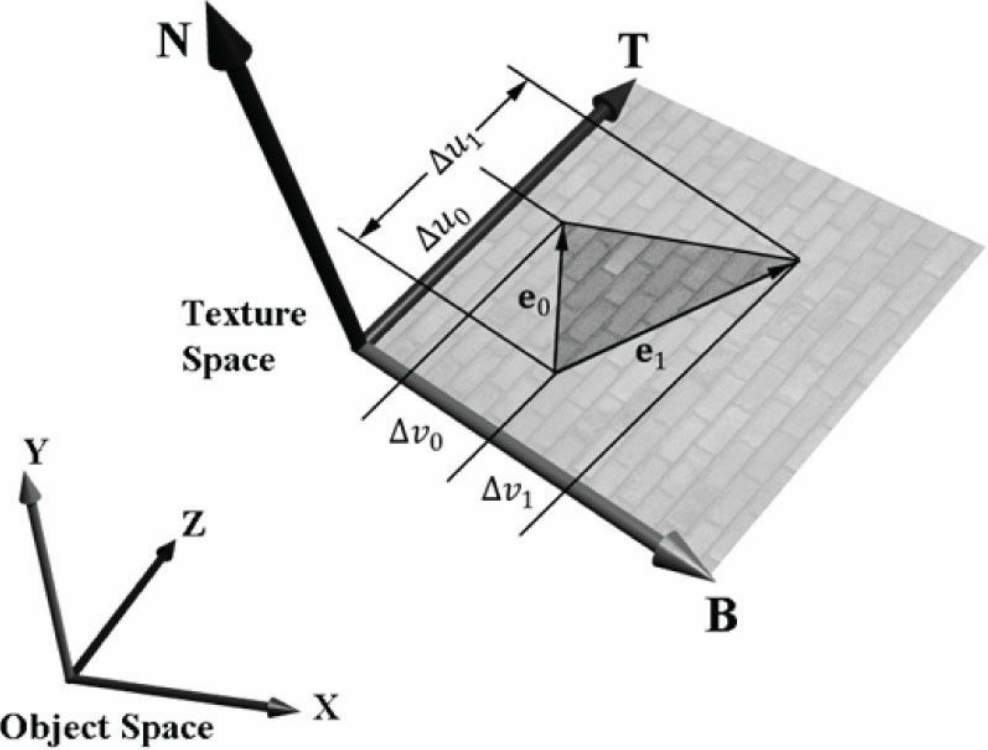
圖片展示了一個三角形與所處的切線空間，我們可以這樣定義向量E0和E1：

\[\mathbf{e_0} = \mathbf{V_1} - \mathbf{V_0}\]
\[\mathbf{e_1} = \mathbf{V_2} - \mathbf{V_0}\]

現在T軸和B軸都是待求的單位向量，可以列出下述關係：

\[(\Delta u_0, \Delta v_0) = (u_1 - u_0, v_1 - v_0)\]
\[(\Delta u_1, \Delta v_1) = (u_2 - u_0, v_2 - v_0)\]
\[\mathbf{e_0} = \Delta u_0\mathbf{T} + \Delta v_0\mathbf{B}\]
\[\mathbf{e_1} = \Delta u_1\mathbf{T} + \Delta v_1\mathbf{B}\]

把它用矩陣來描述：

\[ \begin{bmatrix} \mathbf{e_0} \\ \mathbf{e_1} \end{bmatrix} = \begin{bmatrix} \Delta u_0 & \Delta v_0 \\ \Delta u_1 & \Delta v_1 \end{bmatrix} \begin{bmatrix} \mathbf{T} \\ \mathbf{B} \end{bmatrix} \]

繼續細化：

\[ \begin{bmatrix} e_{0x} & e_{0y} & e_{0z} \\ e_{1x} & e_{1y} & e_{1z} \end{bmatrix} = \begin{bmatrix} \Delta u_0 & \Delta v_0 \\ \Delta u_1 & \Delta v_1 \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} \]

為了計算TB矩陣，需要在等式兩邊左乘uv矩陣的逆：

\[ {\begin{bmatrix} \Delta u_0 & \Delta v_0 \\ \Delta u_1 & \Delta v_1 \end{bmatrix}}^{-1} \begin{bmatrix} e_{0x} & e_{0y} & e_{0z} \\ e_{1x} & e_{1y} & e_{1z} \end{bmatrix} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} \]

對於一個二階矩陣頂點求逆，我們不考慮過程。已知有矩陣\(\mathbf{A} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\)，那麼它的逆矩陣為：

\[ \mathbf{A}^{-1} = \frac{1}{ad-bc}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \]

因此上面的方程最終變成：

\[ \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} = \frac{1}{\Delta u_0 \Delta v_1 - \Delta v_0 \Delta u_1} \begin{bmatrix} \Delta v_1 & - \Delta v_0 \\ -\Delta u_1 & \Delta u_0 \end{bmatrix} \begin{bmatrix} e_{0x} & e_{0y} & e_{0z} \\ e_{1x} & e_{1y} & e_{1z} \end{bmatrix} \]

這裡可以找一個例子嘗試一下：
V0座標為(0, 0, -0.25), 紋理座標為(0, 0.5)
V1座標為(0.15, 0, 0), 紋理座標為(0.3, 0)
V2座標為(0.4, 0, 0), 紋理座標為(0.8, 0)

求解過程如下：
\[ \mathbf{e_0} = \mathbf{V_1} - \mathbf{V_0} = (0.15, 0, 0.25) \]
\[ \mathbf{e_1} = \mathbf{V_2} - \mathbf{V_0} = (0.4, 0, 0.25) \]
\[ (\Delta u_0, \Delta v_0) = (u_1 - u_0, v_1 - v_0) = (0.3, -0.5) \]
\[ (\Delta u_1, \Delta v_1) = (u_2 - u_0, v_2 - v_0) = (0.8, -0.5) \]
\[ \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} = \frac{1}{0.3 \times (-0.5) - (-0.5) \times 0.8} \begin{bmatrix} -0.5 & 0.5 \\ -0.8 & 0.3 \end{bmatrix} \begin{bmatrix} 0.15 & 0 & 0.25 \\ 0.4 & 0 & 0.25 \end{bmatrix} = \begin{bmatrix} 0.5 & 0 & 0 \\ 0 & 0 & -0.5 \end{bmatrix} \]

由於位置座標和紋理座標的不一致性，導致求出來的T向量和B向量很有可能不是單位向量。僅當位置座標的變化率與紋理座標的變化率相同時才會得到單位向量。這裡我們將其進行標準化即可。

但如果對紋理座標進行了變換，有可能導致T軸和B軸不相互垂直。比如嘗試用球體網格模型某個三角形面內的一點對映到球面上一點。

頂點切線空間

上面的運算得到的切線空間是基於單個三角形的，可以看到其運算過程還是比較複雜，而且交給著色器來進行運算的話還會產生大量的指令。

我們可以為頂點新增法向量N和切線向量T用於構建基於頂點的切線空間。很早之前提到法向量是與該頂點共用的所有三角形的法向量取平均值所得到的。切線向量也一樣，它是與該頂點共用的所有三角形的切線向量取平均值所得到的。

現在Vertex.h定義了我們的新頂點型別：

struct VertexPosNormalTangentTex
{
    DirectX::XMFLOAT3 pos;
    DirectX::XMFLOAT3 normal;
    DirectX::XMFLOAT4 tangent;
    DirectX::XMFLOAT2 tex;
    static const D3D11_INPUT_ELEMENT_DESC inputLayout[4];
};

這裡的tangent是一個4D向量，考慮到要和微軟DXTK定義的頂點型別保持一致，多出來的w分量可以留作他用，這裡暫不討論。

施密特向量正交化

通常頂點提供的N和T通常是相互垂直的，並且都是單位向量，我們可以通過計算\(\mathbf{B} = \mathbf{N} \times \mathbf{T}\)來得到副法線向量B，使得頂點可以不需要存放副法線向量B。但是經過插值計算後的N和T可能會導致不是相互垂直，我們最好還是要通過施密特正交化來獲得實際的切線空間。

現在已知互不垂直的N向量和T向量，我們希望求出與N向量垂直的T'向量，需要將T向量投影到N向量上。

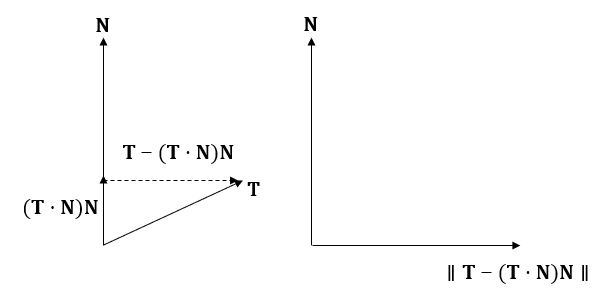
從上面的圖我們可以知道最終求得的T' 為

\[ \mathbf{T'} = \lVert \mathbf{T} - (\mathbf{T} \cdot \mathbf{N}) \mathbf{N} \rVert \]

B' 最終也可以確定下來
\[ \mathbf{B'} = \mathbf{N} \times \mathbf{T'}\]

這樣T', B', N相互垂直，可以構成TBN座標系。在後面的著色器實現中我們也會用到這部分內容。

切線空間的變換

一開始的切線空間可以用一個單位矩陣來表示，切線向量正是處在這個空間中。緊接著就是需要對其進行一次到區域性物件(具體到某個三角形)切線空間的變換：

\[ \mathbf{M}_{object} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \\ N_x & N_y & N_z \end{bmatrix} \]

然後切線向量隨同世界矩陣一同進行變換來到世界座標系，因此我們可以把它寫成：

\[ \mathbf{n}_{world} = \mathbf{n}_{tangent}\mathbf{M}_{object}\mathbf{M}_{world} \]

注意：

1. 對切線向量進行矩陣變換，我們只需要使用3x3的矩陣即可。
2. 法線向量變換到世界矩陣需要用世界矩陣求逆的轉置進行校正，而對切線向量只需要用世界矩陣變換即可。下圖演示了將寬度拉伸為原來2倍後，法線和切線向量的變化：
   

HLSL程式碼

為了使用法線貼圖，我們需要完成下列步驟：

1. 獲取該紋理所需要用到的法線貼圖，在C++端為其建立一個ID3D11Texture2D。這裡不考慮如何製作一張法線貼圖。
2. 對於一個網格模型來說，頂點資料需要包含位置、法向量、切線向量、紋理座標四個元素。同樣這裡不討論模型的製作，在本教程使用的是Geometry所生成的網格模型
3. 在頂點著色器中，將頂點法向量和切線向量從區域性座標系變換到世界座標系
4. 在畫素著色器中，使用經過插值的法向量和切線向量來為每個三角形表面的畫素點構建TBN座標系，然後將切線空間的法向量變換到世界座標系中，這樣最終求得的法向量用於光照計算。

現在我們的Basic.hlsli沿用的是第23章動態天空盒的部分，變化如下：

Texture2D gDiffuseMap : register(t0);
Texture2D gNormalMap : register(t1);
TextureCube gTexCube : register(t2);
SamplerState gSam : register(s0);

// 使用的是第23章的常量緩衝區，省略...
// 省略和之前一樣的結構體...

struct VertexPosNormalTangentTex
{
    float3 PosL : POSITION;
    float3 NormalL : NORMAL;
    float4 TangentL : TANGENT;
    float2 Tex : TEXCOORD;
};

struct InstancePosNormalTangentTex
{
    float3 PosL : POSITION;
    float3 NormalL : NORMAL;
    float4 TangentL : TANGENT;
    float2 Tex : TEXCOORD;
    matrix World : World;
    matrix WorldInvTranspose : WorldInvTranspose;
};

struct VertexPosHWNormalTangentTex
{
    float4 PosH : SV_POSITION;
    float3 PosW : POSITION; // 在世界中的位置
    float3 NormalW : NORMAL; // 法向量在世界中的方向
    float4 TangentW : TANGENT; // 切線在世界中的方向
    float2 Tex : TEXCOORD;
};

float3 NormalSampleToWorldSpace(float3 normalMapSample,
    float3 unitNormalW,
    float4 tangentW)
{
    // 將讀取到法向量中的每個分量從[0, 1]還原到[-1, 1]
    float3 normalT = 2.0f * normalMapSample - 1.0f;

    // 構建位於世界座標系的切線空間
    float3 N = unitNormalW;
    float3 T = normalize(tangentW.xyz - dot(tangentW.xyz, N) * N); // 施密特正交化
    float3 B = cross(N, T);

    float3x3 TBN = float3x3(T, B, N);

    // 將凹凸法向量從切線空間變換到世界座標系
    float3 bumpedNormalW = mul(normalT, TBN);

    return bumpedNormalW;
}

上面的NormalSampleToWorldSpace函式用於將法向量從切線空間變換到世界空間，位於Basic.hlsli。它接受了3個引數：從法線貼圖取樣得到的向量，變換到世界座標系的法向量和切線向量。

然後是頂點著色器：

// NormalMapObject_VS.hlsl
#include "Basic.hlsli"

// 頂點著色器
VertexPosHWNormalTangentTex VS(VertexPosNormalTangentTex vIn)
{
    VertexPosHWNormalTangentTex vOut;
    
    matrix viewProj = mul(gView, gProj);
    vector posW = mul(float4(vIn.PosL, 1.0f), gWorld);

    vOut.PosW = posW.xyz;
    vOut.PosH = mul(posW, viewProj);
    vOut.NormalW = mul(vIn.NormalL, (float3x3) gWorldInvTranspose);
    vOut.TangentW = mul(vIn.TangentL, gWorld);
    vOut.Tex = vIn.Tex;
    return vOut;
}

// NormalMapInstance_VS.hlsl
#include "Basic.hlsli"

// 頂點著色器
VertexPosHWNormalTangentTex VS(InstancePosNormalTangentTex vIn)
{
    VertexPosHWNormalTangentTex vOut;
    
    matrix viewProj = mul(gView, gProj);
    vector posW = mul(float4(vIn.PosL, 1.0f), vIn.World);

    vOut.PosW = posW.xyz;
    vOut.PosH = mul(posW, viewProj);
    vOut.NormalW = mul(vIn.NormalL, (float3x3) vIn.WorldInvTranspose);
    vOut.TangentW = mul(vIn.TangentL, vIn.World);
    vOut.Tex = vIn.Tex;
    return vOut;
}

相比之前的畫素著色器，現在它多了對法線對映的處理：

// 法線對映
float3 normalMapSample = gNormalMap.Sample(gSam, pIn.Tex).rgb;
float3 bumpedNormalW = NormalSampleToWorldSpace(normalMapSample, pIn.NormalW, pIn.TangentW);

求得的法向量bumpedNormalW將用於光照計算。

現在完整的畫素著色器程式碼如下：

// NormalMap_PS.hlsl
#include "Basic.hlsli"

// 畫素著色器(3D)
float4 PS(VertexPosHWNormalTangentTex pIn) : SV_Target
{
    // 若不使用紋理，則使用預設白色
    float4 texColor = float4(1.0f, 1.0f, 1.0f, 1.0f);

    if (gTextureUsed)
    {
        texColor = gDiffuseMap.Sample(gSam, pIn.Tex);
        // 提前進行裁剪，對不符合要求的畫素可以避免後續運算
        clip(texColor.a - 0.1f);
    }
    
    // 標準化法向量
    pIn.NormalW = normalize(pIn.NormalW);

    // 求出頂點指向眼睛的向量，以及頂點與眼睛的距離
    float3 toEyeW = normalize(gEyePosW - pIn.PosW);
    float distToEye = distance(gEyePosW, pIn.PosW);

    // 法線對映
    float3 normalMapSample = gNormalMap.Sample(gSam, pIn.Tex).rgb;
    float3 bumpedNormalW = NormalSampleToWorldSpace(normalMapSample, pIn.NormalW, pIn.TangentW);

    // 初始化為0 
    float4 ambient = float4(0.0f, 0.0f, 0.0f, 0.0f);
    float4 diffuse = float4(0.0f, 0.0f, 0.0f, 0.0f);
    float4 spec = float4(0.0f, 0.0f, 0.0f, 0.0f);
    float4 A = float4(0.0f, 0.0f, 0.0f, 0.0f);
    float4 D = float4(0.0f, 0.0f, 0.0f, 0.0f);
    float4 S = float4(0.0f, 0.0f, 0.0f, 0.0f);
    int i;

    [unroll]
    for (i = 0; i < 5; ++i)
    {
        ComputeDirectionalLight(gMaterial, gDirLight[i], bumpedNormalW, toEyeW, A, D, S);
        ambient += A;
        diffuse += D;
        spec += S;
    }
        
    [unroll]
    for (i = 0; i < 5; ++i)
    {
        ComputePointLight(gMaterial, gPointLight[i], pIn.PosW, bumpedNormalW, toEyeW, A, D, S);
        ambient += A;
        diffuse += D;
        spec += S;
    }

    [unroll]
    for (i = 0; i < 5; ++i)
    {
        ComputeSpotLight(gMaterial, gSpotLight[i], pIn.PosW, bumpedNormalW, toEyeW, A, D, S);
        ambient += A;
        diffuse += D;
        spec += S;
    }
  
    float4 litColor = texColor * (ambient + diffuse) + spec;

    // 反射
    if (gReflectionEnabled)
    {
        float3 incident = -toEyeW;
        float3 reflectionVector = reflect(incident, pIn.NormalW);
        float4 reflectionColor = gTexCube.Sample(gSam, reflectionVector);

        litColor += gMaterial.Reflect * reflectionColor;
    }
    // 折射
    if (gRefractionEnabled)
    {
        float3 incident = -toEyeW;
        float3 refractionVector = refract(incident, pIn.NormalW, gEta);
        float4 refractionColor = gTexCube.Sample(gSam, refractionVector);

        litColor += gMaterial.Reflect * refractionColor;
    }

    litColor.a = texColor.a * gMaterial.Diffuse.a;
    return litColor;
}

所有的著色器將共用Basic.hlsli。而對BasicEffect的變化（和C++的互動）這裡我們不討論。

下面的動畫演示了法線貼圖的對比效果（GIF畫質有點渣）：

至此進階篇就告一段落了。

DirectX11 With Windows SDK完整目錄

Github專案原始碼