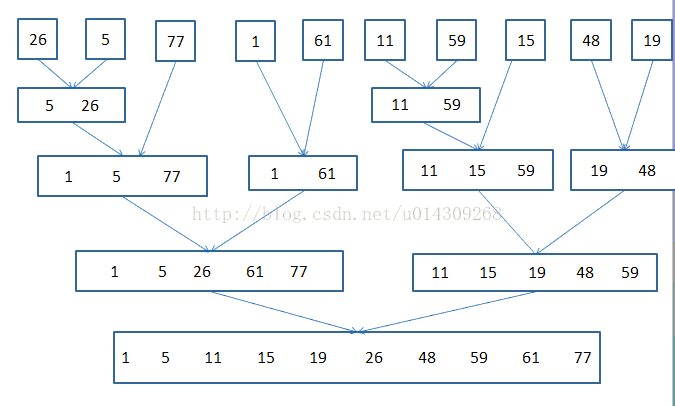
下面這圖展示了二路歸併的過程

二路歸併的核心程式碼是merge（）函式

它將2個分割的陣列有序的合併在一起

如圖：

在陣列A中，

從p到q是一個數組，從q到r是另外一個數組

那麼如何將這2個數組有序的合併在一起，組個新的陣列A呢？

步驟：

第一步：開闢一個數組L，存放p到q之間（也就是需要歸併的左邊陣列）的元素

第二部：開闢一個數組R，存放q到r之間（也就是需要歸併的右邊陣列）的元素

第三步：2個數組的最後還要加一個無窮大的數（可以用0x7FFF表示），因此開闢的陣列空間要多1字元個空間

第四步：L與R中的數字逐個比較，把較小的先放在陣列A中（從陣列A【0】開始存放，依次往後覆蓋原來的數），然後較小的陣列指標往後移動，指向下一位再和另外一個數組比較

//第一個引數為需要排序的陣列，第2個引數為分割的第一個陣列開始元素的下標
//第3個引數為分割的第一個陣列的最後1個元素的下標
//第4個引數為陣列最後1個元素的下標
void Merge(int *A,int p,int q,int r)
{
	int n1,n2,i,j,k,g;
	n1=q-p+1;
	n2=r-q;
	int *L,*R;
	L=(int *)malloc(sizeof(int)*(n1+1)); 
	R=(int *)malloc(sizeof(int)*(n2+1));
	L[n1]=0x7fff; //開闢的左右2個數組最後1個數設定為最大值
	R[n2]=0x7fff;
	g=0;
	for(i=p;i<=q;i++)
	{
		L[g]=A[i];
		g++;
	}
	g=0;
	for(i=q+1;i<=r;i++)
	{
		R[g]=A[i];
		g++;
	}
	//逐個比較左右兩組陣列，把較小的值寫入原來的陣列
	j=k=0;
	for(i=p;i<=r;i++)
	{
		if(L[j]<R[k])
		{
			A[i]=L[j];
			j++;
		}
		else
		{
			A[i]=R[k];
			k++;
		}
	}
}
 

#include<iostream>
using namespace std;

//第一個引數為需要排序的陣列，第2個引數為分割的第一個陣列開始元素的下標
//第3個引數為分割的第一個陣列的最後1個元素的下標
//第4個引數為陣列最後1個元素的下標
void Merge(int *A,int p,int q,int r)
{
	int n1,n2,i,j,k,g;
	n1=q-p+1;
	n2=r-q;
	int *L,*R;
	L=(int *)malloc(sizeof(int)*(n1+1)); 
	R=(int *)malloc(sizeof(int)*(n2+1));
	L[n1]=0x7fff; //開闢的左右2個數組最後1個數設定為最大值
	R[n2]=0x7fff;
	g=0;
	for(i=p;i<=q;i++)
	{
		L[g]=A[i];
		g++;
	}
	g=0;
	for(i=q+1;i<=r;i++)
	{
		R[g]=A[i];
		g++;
	}
	//逐個比較左右兩組陣列，把較小的值寫入原來的陣列
	j=k=0;
	for(i=p;i<=r;i++)
	{
		if(L[j]<R[k])
		{
			A[i]=L[j];
			j++;
		}
		else
		{
			A[i]=R[k];
			k++;
		}
	}
}

void MergeSort(int *A,int p,int r)
{
	int q;
	if(p<r) //當第一個元素比最後1個元素還小時，繼續執行遞迴，直到只剩下一個元素（形參p=r）
	{
	q=(p+r)/2;
	MergeSort(A,p,q);
	MergeSort(A,q+1,r);
	Merge(A,p,q,r);
	}
}

void main()
{
	int A[5]={5,3,4,23,11};
	MergeSort(A,0,4);
	for(int i=0;i<5;i++)
		cout<<A[i]<<endl;
	system("pause");
}