這一塊的每一個小點都可以引申出很多的東西，所以先做一個大概，用以備忘，持續更新。
*一般過程：
（1）資料採集
資料採集是最基本也很耗時間的工作。比如對於具體的工程事件，需要考慮採集哪些型別的資料？需要哪些屬性？需要多少資料支撐？然後再實際去採集這些資料，離線採集？線上獲取？

（2）資料預處理
基於最後期望的目標結果，對於當前的資料，如何處理當前的資料型別，比如如何處理有序變數？如何處理無序變數？資料可信嗎？有缺失值嗎？應該正則化嗎？離群值，噪音點怎麼處理？特徵工程？偏差檢測？樣本過濾？等等等等，資料清洗將會耗去大量的時間。

（3）解釋模型結果和調整模型
根據資料，選用合適的模型，然後不斷的根據結果微調模型，改進模型。或是在發現某些問題後，再返回第二步，重做第三步。不斷的評估模型以完成最好的結果。

如何進行特徵選擇？
PCA：尋找表示資料分佈的最優子空間，將原始資料降維，並提取不相關的部分。
LDA：尋找可分性判據最大的子空間。使得降維後類內散度最小，類間散度最大
ICA：將原始資料降維並提取出相互獨立的屬性，ICA理論的目標就是通過X求得一個分離矩陣W，使得W作用在X上所獲得的訊號Y是獨立源S的最優逼近。ICA相比與PCA更能刻畫變數的隨機統計特性，且能抑制高斯噪聲。
CCA，找到兩組基，使得兩組資料在這兩組基上的投影相關性最大，用來描述兩個高維變數之間的線性關係

特徵選擇：
包裹式：把最終機器學習模型的表現作為特徵選擇的重要依據，一步步篩選特徵。目前比較常用的一種包裹式特徵選擇法為遞迴特徵消除法，其原理是使用一個基模型（如：隨機森林、邏輯迴歸等）進行多輪訓練，每輪訓練結束後，消除若干權值係數較低的特徵，再基於新的特徵集進行新的一輪訓練。
過濾式

資料壓縮–三大降維法則：
主成分分析，自編碼，t-SNE等。

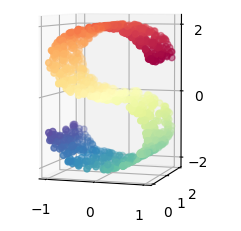
@@@PCA是一種線性演算法。 它不能解釋特徵之間的複雜多項式關係。而t-SNE是基於在鄰域圖上隨機遊走的概率分佈，可以在資料中找到其區域性結構關係，最先出現在流型學習中，演算法核心在於它的“距離”度量，即它將資料點之間的相似度轉換為概率，以

import numpy as np
from sklearn.manifold import TSNE
X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])#簡單的三維資料
tsne = TSNE(n_components=2)
tsne.fit_transform(X)
print(tsne.embedding_)

from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets

n_points = 1000
X, color = datasets.samples_generator.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2

ax = fig.add_subplot(211, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
ax.view_init(4, -72)  # 自定義3D顯示視角

t0 = time()
tsne = manifold.TSNE(n_components=n_components, init='pca', random_state=0)#使用TSNE
Y = tsne.fit_transform(X) 
t1 = time()#計算時間，可以看到號稱最好降維技術的TNSE在使用時的最大弊病
print("t-SNE: %.2g sec" % (t1 - t0))  
ax = fig.add_subplot(2, 1, 2)
plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter()) # 設定標籤顯示為空
ax.yaxis.set_major_formatter(NullFormatter())

plt.show()

@@@PCA 和 t-SNE 是方法，而自編碼器則是一系列的方法（中間層可以自由任我們設定與控制）。

如何資料預處理？
目標是：準確性，完整性，一致性，時效性，可信性，可解釋性。

資料清洗：處理缺失值，光滑噪音資料，識別離群點，錯誤點，修正邏輯。
【多用聚類和異常點檢測】
資料整合：多個數據源可能對同一屬性有不同的名字而造成的冗餘，衝突值，重複項等。
資料規約：降維，資料壓縮，數量規約，以簡化資料集。
資料變換：規範化，資料離散化，概念分層，粒度，資料型別變換，屬性構造。
【不平衡採用取樣法或者權重法】

具體方法有：
歸一化：對資料集進行區間縮放，縮放到[0,1]的區間內，把有單位的資料轉化為沒有單位的資料，即統一資料的衡量標準，消除單位的影響。

from sklearn import preprocessing#使用preprocessing
import numpy as np
X = [[ 1., -1.,  2.],
      [ 2.,  0.,  0.],
      [ 0.,  1., -1.]]
X_normalized = preprocessing.normalize(X, norm='l2')
print(X_normalized)

normalizer = preprocessing.Normalizer().fit(X)  #以便之後對測試集進行相同的轉換
normalizer.transform([[-1.,  1., 0.]]) 

輸出為：
array([[ 0.40824829, -0.40824829, 0.81649658],
[ 1. , 0. , 0. ],
[ 0. , 0.70710678, -0.70710678]])
array([[-0.70710678, 0.70710678, 0. ]])

標準化：標準化是在不改變原資料分佈的前提下，將資料按比例縮放，使之落入一個限定的區間，使資料之間具有可比性。如有：【但是實際上這樣通常忽略分佈的具體形態，資料轉換僅指，減去每個特徵的平均值，再除以他們的標準差。】
1.z-score標準化：這是最常見的特徵預處理方式，基本所有的線性模型在擬合的時候都會做 z-score標準化。具體的方法是求出樣本特徵x的均值mean和標準差std，然後用（x-mean)/std來代替原特徵。這樣特徵就變成了均值為0，方差為1了。在sklearn中，我們可以用StandardScaler來做z-score標準化。當然，如果我們是用pandas做資料預處理，可以自己在資料框裡面減去均值，再除以方差，自己做z-score標準化。
2.max-min標準化：也稱為離差標準化，預處理後使特徵值對映到[0,1]之間。具體的方法是求出樣本特徵x的最大值max和最小值min，然後用(x-min)/(max-min)來代替原特徵。如果我們希望將資料對映到任意一個區間[a,b]，而不是[0,1]，那麼也很簡單。用(x-min)(b-a)/(max-min)+a來代替原特徵即可。在sklearn中，我們可以用MinMaxScaler來做max-min標準化。這種方法的問題就是如果測試集或者預測資料裡的特徵有小於min，或者大於max的資料，會導致max和min發生變化，需要重新計算。所以實際演算法中， 除非你對特徵的取值區間有需求，否則max-min標準化沒有 z-score標準化好用。
3.L1/L2範數標準化：通常情況下，範數標準化首選L2範數標準化。在sklearn中，我們可以用Normalizer來做L1/L2範數標準化。

from sklearn import preprocessing#使用preprocessing
import numpy as np
X = np.array([[ 1., -1.,  2.],
               [ 2.,  0.,  0.],
               [ 0.,  1., -1.]])
X_scaled = preprocessing.scale(X)
print(X_scaled)       
print(X_scaled.mean(axis=0))          
print(X_scaled.std(axis=0))

scaler = preprocessing.StandardScaler().fit(X)#計算訓練集的平均值和標準差，以便之後對測試集進行相同的轉換。
print(scaler.transform([[-1.,  1., 0.]]) )

輸出結果為：
array([[ 0. , -1.22474487, 1.33630621],
[ 1.22474487, 0. , -0.26726124],
[-1.22474487, 1.22474487, -1.06904497]])
調整後的資料平均值為0，方差為1。
array([ 0., 0., 0.])
array([ 1., 1., 1.])
array([[-2.44948974, 1.22474487, -0.26726124]])

離散化：把連續的數值型特徵進行分段，將落在每一個分段內的資料賦予一個新的統一的符號或數值。可採用相等步長或相等頻率等方式進行離散化。

二值化：將數值型資料轉換為0和1兩個值，例如通過設定一個閾值，當特徵的值大於該閾值時，轉換為1，小於或等於該閾值時轉換為0。二值化的目的在於簡化資料，有些時候還可以消除資料中的“雜音”，例如影象資料。

from sklearn import preprocessing#使用preprocessing
import numpy as np
X = [[ 1., -1.,  2.],
      [ 2.,  0.,  0.],
      [ 0.,  1., -1.]]
binarizer = preprocessing.Binarizer().fit(X) 
binarizer.transform(X)

binarizer = preprocessing.Binarizer(threshold=1.1)#預設閾值為0
binarizer.transform(X)

修改閾值可以看到：
array([[ 1., 0., 1.],
[ 1., 0., 0.],
[ 0., 1., 0.]])
array([[ 0., 0., 1.],
[ 1., 0., 0.],
[ 0., 0., 0.]])

啞編碼：One-Hot Encoding，其作用是將特徵進行量化。

from sklearn import preprocessing#使用preprocessing
import numpy as np
enc = preprocessing.OneHotEncoder()
enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]])  
enc.transform([[0, 1, 3]]).toarray()#自動提取

enc = preprocessing.OneHotEncoder(n_values=[2, 3, 4])#防止丟失值，明確設定value。如此處特徵分別有2，3，4個值
enc.fit([[1, 2, 3], [0, 2, 0]])
enc.transform([[1, 0, 0]]).toarray()

array([[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]])
array([[ 0., 1., 1., 0., 0., 1., 0., 0., 0.]])

**如何處理缺失資料? **
產生原因：資料無法獲取，被遺漏，屬性不可用，或者不重要等。
解決方法：
1.刪除缺失行。從而得到一個完備的資訊表。以資料量來換取資訊的完備，會造成資源的大量浪費，而且丟棄了大量隱藏資訊，甚至是某些很重要的資訊

2.人工填寫。特殊全域性常量值，平均值，尋找最相似的物件補齊，K近鄰平均補齊，迴歸，EM，尋找屬性間的關係（決策樹），所有的可能值填充。

import numpy as np
from sklearn.preprocessing import Imputer
imp = Imputer(missing_values='NaN', strategy='mean', axis=0)#缺失值由平均值處理
imp.fit([[1, 2], [np.nan, 3], [7, 6]])
Imputer(axis=0, copy=True, missing_values='NaN', strategy='mean', verbose=0)
X = [[np.nan, 2], [6, np.nan], [7, 6]]
print(imp.transform(X))    

3.不處理。貝葉斯網路和神經網路.

*如何評估模型？

效能度量：
正確率，錯誤率，查全率，查準率，F1
方差，誤差，R平均值。
ROC曲線
AUC(ROC曲線下面積)
Lift(提升)和Gain(增益)
K-S圖
基尼係數

*如何處理稀疏資料？
流型降維，資料平滑。

import scipy.sparse as sp
X = sp.csc_matrix([[1, 2], [0, 3], [7, 6]])
imp = Imputer(missing_values=0, strategy='mean', axis=0)#Imputer也支援稀疏矩陣
imp.fit(X)
X_test = sp.csc_matrix([[0, 2], [6, 0], [7, 6]])
print(imp.transform(X_test)) 

[[ 4. 2. ]
[ 6. 3.66666667]
[ 7. 6. ]]
但是這裡的缺失值被編碼為0，被隱性地儲存在了矩陣中。當缺失值個數比觀察值多很多的時候，這個形式才比較適用。