邏輯迴歸

1 二元邏輯迴歸

  迴歸是一種很容易理解的模型，就相當於y=f(x)，表明自變數x與因變數y的關係。最常見問題如醫生治病時的望、聞、問、切，之後判定病人是否生病或生了什麼病，
其中的望、聞、問、切就是獲取的自變數x，即特徵資料，判斷是否生病就相當於獲取因變數y，即預測分類。最簡單的迴歸是線性迴歸，但是線性迴歸的魯棒性很差。

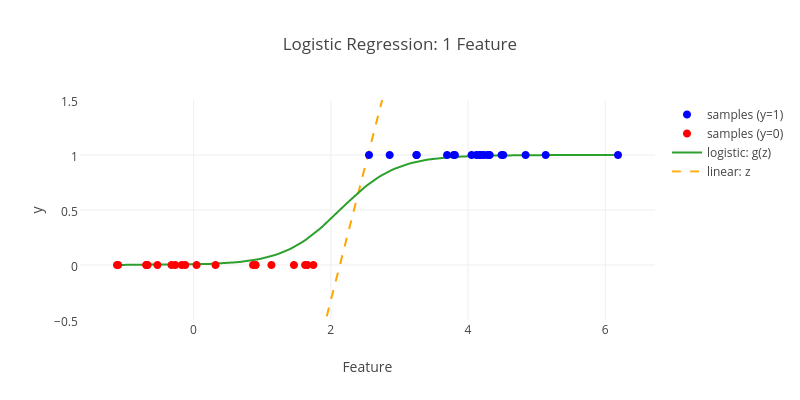
  邏輯迴歸是一種減小預測範圍，將預測值限定為[0,1]間的一種迴歸模型，其迴歸方程與迴歸曲線如下圖所示。邏輯曲線在z=0時，十分敏感，在z>>0或z<<0時，都不敏感。

  邏輯迴歸其實是線上性迴歸的基礎上，套用了一個邏輯函式。上圖的`g(z)`就是這個邏輯函式(或稱為`Sigmoid`函式)。下面左圖是一個線性的決策邊界，右圖是非線性的決策邊界。
  對於線性邊界的情況，邊界形式可以歸納為如下公式**(1)**:
  因此我們可以構造預測函式為如下公式**(2)**:
  該預測函式表示分類結果為1時的概率。因此對於輸入點`x`，分類結果為類別1和類別0的概率分別為如下公式**(3)**：
  對於訓練資料集，特徵資料`x={x1, x2, … , xm}`和對應的分類資料`y={y1, y2, … , ym}`。構建邏輯迴歸模型`f`，最典型的構建方法便是應用極大似然估計。對公式**(3)**取極大似然函式，可以得到如下的公式**(4)**:
  再對公式**(4)**取對數，可得到公式**(5)**：
  最大似然估計就是求使`l`取最大值時的`theta`。`MLlib`中提供了兩種方法來求這個引數，分別是[梯度下降法](https://github.com/endymecy/spark-ml-source-analysis/blob/master/%E6%9C%80%E4%BC%98%E5%8C%96%E7%AE%97%E6%B3%95/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D/gradient-descent.md)和[L-BFGS](https://github.com/endymecy/spark-ml-source-analysis/blob/master/%E6%9C%80%E4%BC%98%E5%8C%96%E7%AE%97%E6%B3%95/L-BFGS/lbfgs.md)。

2 多元邏輯迴歸

  二元邏輯迴歸可以一般化為多元邏輯迴歸用來訓練和預測多分類問題。對於多分類問題，演算法將會訓練出一個多元邏輯迴歸模型，
它包含K-1個二元迴歸模型。給定一個數據點，K-1個模型都會執行，概率最大的類別將會被選為預測類別。

  對於輸入點x，分類結果為各類別的概率分別為如下公式(6)，其中k表示類別個數。

  對於`k`類的多分類問題，模型的權重`w = (w_1, w_2, …, w_{K-1})`是一個矩陣，如果新增截距，矩陣的維度為`(K-1) * (N+1)`，否則為`(K-1) * N`。單個樣本的目標函式的損失函式可以寫成如下公式**(7)**的形式。
  對損失函式求一階導數，我們可以得到下面的公式**(8)**:
  根據上面的公式，如果某些`margin`的值大於709.78，`multiplier`以及邏輯函式的計算會出現算術溢位(`arithmetic overflow`)的情況。這個問題發生在有離群點遠離超平面的情況下。 幸運的是，當`max(margins) = maxMargin > 0`時，損失函式可以重寫為如下公式**(9)**的形式。
  同理，`multiplier`也可以重寫為如下公式**(10)**的形式。

3 邏輯迴歸的優缺點

• 優點：計算代價低，速度快，容易理解和實現。
• 缺點：容易欠擬合，分類和迴歸的精度不高。

4 例項

  下面的例子展示瞭如何使用邏輯迴歸。

import org.apache.spark.SparkContext
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionModel}
import org.apache.spark.mllib.evaluation.MulticlassMetrics
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils
// 載入訓練資料
val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")
// 切分資料，training (60%) and test (40%).
val splits = data.randomSplit(Array(0.6, 0.4), seed = 11L)
val training = splits(0).cache()
val test = splits(1)
// 訓練模型
val model = new LogisticRegressionWithLBFGS()
  .setNumClasses(10)
  .run(training)
// Compute raw scores on the test set.
val predictionAndLabels = test.map { case LabeledPoint(label, features) =>
  val prediction = model.predict(features)
  (prediction, label)
}
// Get evaluation metrics.
val metrics = new MulticlassMetrics(predictionAndLabels)
val precision = metrics.precision
println("Precision = " + precision)
// 儲存和載入模型
model.save(sc, "myModelPath")
val sameModel = LogisticRegressionModel.load(sc, "myModelPath")

5 原始碼分析

5.1 訓練模型

  如上所述，在MLlib中，分別使用了梯度下降法和L-BFGS實現邏輯迴歸引數的計算。這兩個演算法的實現我們會在最優化章節介紹，這裡我們介紹公共的部分。

  LogisticRegressionWithLBFGS和LogisticRegressionWithSGD的入口函式均是GeneralizedLinearAlgorithm.run，下面詳細分析該方法。

def run(input: RDD[LabeledPoint]): M = {
    if (numFeatures < 0) {
      //計算特徵數
      numFeatures = input.map(_.features.size).first()
    }
    val initialWeights = {
          if (numOfLinearPredictor == 1) {
            Vectors.zeros(numFeatures)
          } else if (addIntercept) {
            Vectors.zeros((numFeatures + 1) * numOfLinearPredictor)
          } else {
            Vectors.zeros(numFeatures * numOfLinearPredictor)
          }
    }
    run(input, initialWeights)
}

  上面的程式碼初始化權重向量，向量的值均初始化為0。需要注意的是，addIntercept表示是否新增截距(Intercept，指函式圖形與座標的交點到原點的距離)，預設是不新增的。numOfLinearPredictor表示二元邏輯迴歸模型的個數。
我們重點看run(input, initialWeights)的實現。它的實現分四步。

5.1.1 根據提供的引數縮放特徵並新增截距

val scaler = if (useFeatureScaling) {
      new StandardScaler(withStd = true, withMean = false).fit(input.map(_.features))
    } else {
      null
    }
val data =
      if (addIntercept) {
        if (useFeatureScaling) {
          input.map(lp => (lp.label, appendBias(scaler.transform(lp.features)))).cache()
        } else {
          input.map(lp => (lp.label, appendBias(lp.features))).cache()
        }
      } else {
        if (useFeatureScaling) {
          input.map(lp => (lp.label, scaler.transform(lp.features))).cache()
        } else {
          input.map(lp => (lp.label, lp.features))
        }
      }
val initialWeightsWithIntercept = if (addIntercept && numOfLinearPredictor == 1) {
      appendBias(initialWeights)
    } else {
      /** If `numOfLinearPredictor > 1`, initialWeights already contains intercepts. */
      initialWeights
    }

  在最優化過程中，收斂速度依賴於訓練資料集的條件數(condition number)，縮放變數經常可以啟發式地減少這些條件數，提高收斂速度。不減少條件數，一些混合有不同範圍列的資料集可能不能收斂。
在這裡使用StandardScaler將資料集的特徵進行縮放。詳細資訊請看StandardScaler。appendBias方法很簡單，就是在每個向量後面加一個值為1的項。

def appendBias(vector: Vector): Vector = {
    vector match {
      case dv: DenseVector =>
        val inputValues = dv.values
        val inputLength = inputValues.length
        val outputValues = Array.ofDim[Double](inputLength + 1)
        System.arraycopy(inputValues, 0, outputValues, 0, inputLength)
        outputValues(inputLength) = 1.0
        Vectors.dense(outputValues)
      case sv: SparseVector =>
        val inputValues = sv.values
        val inputIndices = sv.indices
        val inputValuesLength = inputValues.length
        val dim = sv.size
        val outputValues = Array.ofDim[Double](inputValuesLength + 1)
        val outputIndices = Array.ofDim[Int](inputValuesLength + 1)
        System.arraycopy(inputValues, 0, outputValues, 0, inputValuesLength)
        System.arraycopy(inputIndices, 0, outputIndices, 0, inputValuesLength)
        outputValues(inputValuesLength) = 1.0
        outputIndices(inputValuesLength) = dim
        Vectors.sparse(dim + 1, outputIndices, outputValues)
      case _ => throw new IllegalArgumentException(s"Do not support vector type ${vector.getClass}")
    }

5.1.2 使用最優化演算法計算最終的權重值

val weightsWithIntercept = optimizer.optimize(data, initialWeightsWithIntercept)

  有梯度下降演算法和L-BFGS兩種演算法來計算最終的權重值，檢視梯度下降法和L-BFGS瞭解詳細實現。
這兩種演算法均使用Gradient的實現類計算梯度，使用Updater的實現類更新引數。在 LogisticRegressionWithSGD 和 LogisticRegressionWithLBFGS 中，它們均使用 LogisticGradient 實現類計算梯度，使用 SquaredL2Updater 實現類更新引數。

//在GradientDescent中
private val gradient = new LogisticGradient()
private val updater = new SquaredL2Updater()
override val optimizer = new GradientDescent(gradient, updater)
    .setStepSize(stepSize)
    .setNumIterations(numIterations)
    .setRegParam(regParam)
    .setMiniBatchFraction(miniBatchFraction)
//在LBFGS中
override val optimizer = new LBFGS(new LogisticGradient, new SquaredL2Updater)

  下面將詳細介紹LogisticGradient的實現和SquaredL2Updater的實現。

• LogisticGradient

  LogisticGradient中使用compute方法計算梯度。計算分為兩種情況，即二元邏輯迴歸的情況和多元邏輯迴歸的情況。雖然多元邏輯迴歸也可以實現二元分類，但是為了效率，compute方法仍然實現了一個二元邏輯迴歸的版本。

val margin = -1.0 * dot(data, weights)
val multiplier = (1.0 / (1.0 + math.exp(margin))) - label
//y += a * x，即cumGradient += multiplier * data
axpy(multiplier, data, cumGradient)
if (label > 0) {
    // The following is equivalent to log(1 + exp(margin)) but more numerically stable.
    MLUtils.log1pExp(margin)
} else {
    MLUtils.log1pExp(margin) - margin
}

  這裡的multiplier就是上文的公式(2)。axpy方法用於計算梯度，這裡表示的意思是h(x) * x。下面是多元邏輯迴歸的實現方法。

//權重
val weightsArray = weights match {
    case dv: DenseVector => dv.values
    case _ =>
            throw new IllegalArgumentException
}
//梯度
val cumGradientArray = cumGradient match {
    case dv: DenseVector => dv.values
    case _ =>
        throw new IllegalArgumentException
}
// 計算所有類別中最大的margin
var marginY = 0.0
var maxMargin = Double.NegativeInfinity
var maxMarginIndex = 0
val margins = Array.tabulate(numClasses - 1) { i =>
    var margin = 0.0
    data.foreachActive { (index, value) =>
        if (value != 0.0) margin += value * weightsArray((i * dataSize) + index)
    }
    if (i == label.toInt - 1) marginY = margin
    if (margin > maxMargin) {
            maxMargin = margin
            maxMarginIndex = i
    }
    margin
}
//計算sum，保證每個margin都小於0，避免出現算術溢位的情況
val sum = {
     var temp = 0.0
     if (maxMargin > 0) {
         for (i <- 0 until numClasses - 1) {
              margins(i) -= maxMargin
              if (i == maxMarginIndex) {
                temp += math.exp(-maxMargin)
              } else {
                temp += math.exp(margins(i))
              }
         }
     } else {
         for (i <- 0 until numClasses - 1) {
              temp += math.exp(margins(i))
         }
     }
     temp
}
//計算multiplier並計算梯度
for (i <- 0 until numClasses - 1) {
     val multiplier = math.exp(margins(i)) / (sum + 1.0) - {
          if (label != 0.0 && label == i + 1) 1.0 else 0.0
     }
     data.foreachActive { (index, value) =>
         if (value != 0.0) cumGradientArray(i * dataSize + index) += multiplier * value
     }
}
//計算損失函式,
val loss = if (label > 0.0) math.log1p(sum) - marginY else math.log1p(sum)
if (maxMargin > 0) {
     loss + maxMargin
} else {
     loss
}

• SquaredL2Updater

class SquaredL2Updater extends Updater {
  override def compute(
      weightsOld: Vector,
      gradient: Vector,
      stepSize: Double,
      iter: Int,
      regParam: Double): (Vector, Double) = {
    // w' = w - thisIterStepSize * (gradient + regParam * w)
    // w' = (1 - thisIterStepSize * regParam) * w - thisIterStepSize * gradient
    //表示步長，即負梯度方向的大小
    val thisIterStepSize = stepSize / math.sqrt(iter)
    val brzWeights: BV[Double] = weightsOld.toBreeze.toDenseVector
    //正則化，brzWeights每行資料均乘以(1.0 - thisIterStepSize * regParam)
    brzWeights :*= (1.0 - thisIterStepSize * regParam)
    //y += x * a，即brzWeights -= gradient * thisInterStepSize
    brzAxpy(-thisIterStepSize, gradient.toBreeze, brzWeights)
    //正則化||w||_2
    val norm = brzNorm(brzWeights, 2.0)
    (Vectors.fromBreeze(brzWeights), 0.5 * regParam * norm * norm)
  }
}

  該函式的實現規則是：

w' = w - thisIterStepSize * (gradient + regParam * w)
w' = (1 - thisIterStepSize * regParam) * w - thisIterStepSize * gradient

  這裡thisIterStepSize表示引數沿負梯度方向改變的速率，它隨著迭代次數的增多而減小。

5.1.3 對最終的權重值進行後處理

val intercept = if (addIntercept && numOfLinearPredictor == 1) {
      weightsWithIntercept(weightsWithIntercept.size - 1)
    } else {
      0.0
    }
var weights = if (addIntercept && numOfLinearPredictor == 1) {
      Vectors.dense(weightsWithIntercept.toArray.slice(0, weightsWithIntercept.size - 1))
    } else {
      weightsWithIntercept
    }

  該段程式碼獲得了截距（intercept）以及最終的權重值。由於截距（intercept）和權重是在收縮的空間進行訓練的，所以我們需要再把它們轉換到原始的空間。數學知識告訴我們，如果我們僅僅執行標準化而沒有減去均值，即withStd = true, withMean = false，
那麼截距（intercept）的值並不會傳送改變。所以下面的程式碼僅僅處理權重向量。

if (useFeatureScaling) {
      if (numOfLinearPredictor == 1) {
        weights = scaler.transform(weights)
      } else {
        var i = 0
        val n = weights.size / numOfLinearPredictor
        val weightsArray = weights.toArray
        while (i < numOfLinearPredictor) {
          //排除intercept
          val start = i * n
          val end = (i + 1) * n - { if (addIntercept) 1 else 0 }
          val partialWeightsArray = scaler.transform(
            Vectors.dense(weightsArray.slice(start, end))).toArray
          System.arraycopy(partialWeightsArray, 0, weightsArray, start, partialWeightsArray.size)
          i += 1
        }
        weights = Vectors.dense(weightsArray)
      }
    }

5.1.4 建立模型

createModel(weights, intercept)

5.2 預測

  訓練完模型之後，我們就可以通過訓練的模型計算得到測試資料的分類資訊。predictPoint用來預測分類資訊。它針對二分類和多分類，分別進行處理。

• 二分類的情況

val margin = dot(weightMatrix, dataMatrix) + intercept
val score = 1.0 / (1.0 + math.exp(-margin))
threshold match {
    case Some(t) => if (score > t) 1.0 else 0.0
    case None => score
}

  我們可以看到1.0 / (1.0 + math.exp(-margin))就是上文提到的邏輯函式即sigmoid函式。

• 多分類情況

var bestClass = 0
var maxMargin = 0.0
val withBias = dataMatrix.size + 1 == dataWithBiasSize
(0 until numClasses - 1).foreach { i =>
        var margin = 0.0
        dataMatrix.foreachActive { (index, value) =>
          if (value != 0.0) margin += value * weightsArray((i * dataWithBiasSize) + index)
        }
        // Intercept is required to be added into margin.
        if (withBias) {
          margin += weightsArray((i * dataWithBiasSize) + dataMatrix.size)
        }
        if (margin > maxMargin) {
          maxMargin = margin
          bestClass = i + 1
        }
}
bestClass.toDouble

  該段程式碼計算並找到最大的margin。如果maxMargin為負，那麼第一類是該資料的類別。

參考文獻

【2】邏輯迴歸