熄燈問題poj1222【列舉】
Description
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
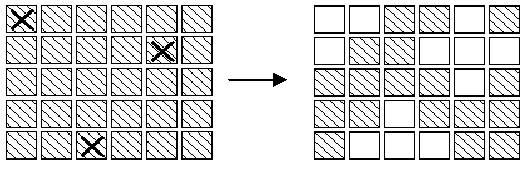
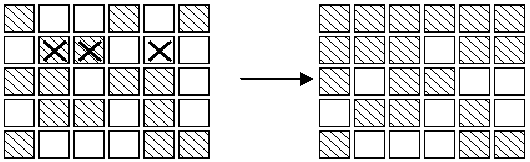
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
Sample Output
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
題意:
有T組 5*6的燈陣,用1表示燈亮,0表示燈滅。每個燈的位置有一個開關,剛開始開關全是關的,用0表示開關關,用1表示開關開。每次切換開關的狀態(即從1->0或從0->1 ) 會改變這個開關上下左右四個位置上燈的狀態,燈亮則滅,燈滅則亮(如果有)。要求給讓每組 所有燈都熄滅時的開關的狀態。
注意:
對同一個開關操作第二次會抵消第一次的操作,而進行三次操作相當於只進行一次操作。所以對同一個開關驚醒多次操作是沒有意義的。
程式碼:
#include <iostream>
using namespace std;
char oriLights[5];
char lights[5];
char result[5];
int GetBit(char c,int i)
{
return (c >> i) & 1 ;
}
void SetBit(char &c,int i,int v)
{
if( v)
c |= (1 << i);
else
c &= ~(1 << i);
}
void FlipBit(char &c,int i)
{
c ^= (1 << i);
}
void OutputResult(int t,char result[])
{
cout << "PUZZLE #" << t << endl;
for(int i=0;i<5;i++)
{
for(int j=0;j<6;j++)
{
cout << GetBit(result[i],j);
if(j < 5)
cout << " ";
}
cout << endl;
}
}
int main()
{
int T;
cin >> T;
for(int t=1;t<=T;t++)
{
for(int i=0;i<5;i++)
for(int j=0;j<6;j++){
int s;
cin >> s;
SetBit(oriLights[i],j,s);
}
for(int n=0;n<64;n++) // 每一行開關有64種可能,對應十進位制數為 0~63
{
int switchs = n;
memcpy(lights,oriLights,sizeof(oriLights)); //
for(int i=0;i<5;i++)
{
result[i] = switchs;
for(int j=0;j<6;j++)
{
if(GetBit(switchs,j))
{
if(j > 0)
FlipBit(lights[i],j-1);
FlipBit(lights[i],j);
if(j < 5)
FlipBit(lights[i],j+1);
}
}
if(i < 4)
lights[i+1] ^= switchs; // 位
switchs = lights[i]; // *** 為了讓第i行亮著的燈熄滅,即在確定第i+1行的燈狀態後,第i行的燈已全部熄滅
}
if(lights[4] == 0)
{
OutputResult(t,result);
break;
}
}
}
return 0;
} 