本文希望闡述堆排序O(nlogn)的一些關鍵細節，摘錄一篇博文O(n^2)進行比較。

堆排序的特點是優化後的選擇排序，其時間複雜度為O(nlogn),下面第一段程式碼的做法比這個複雜度要高。原因在下文闡述。

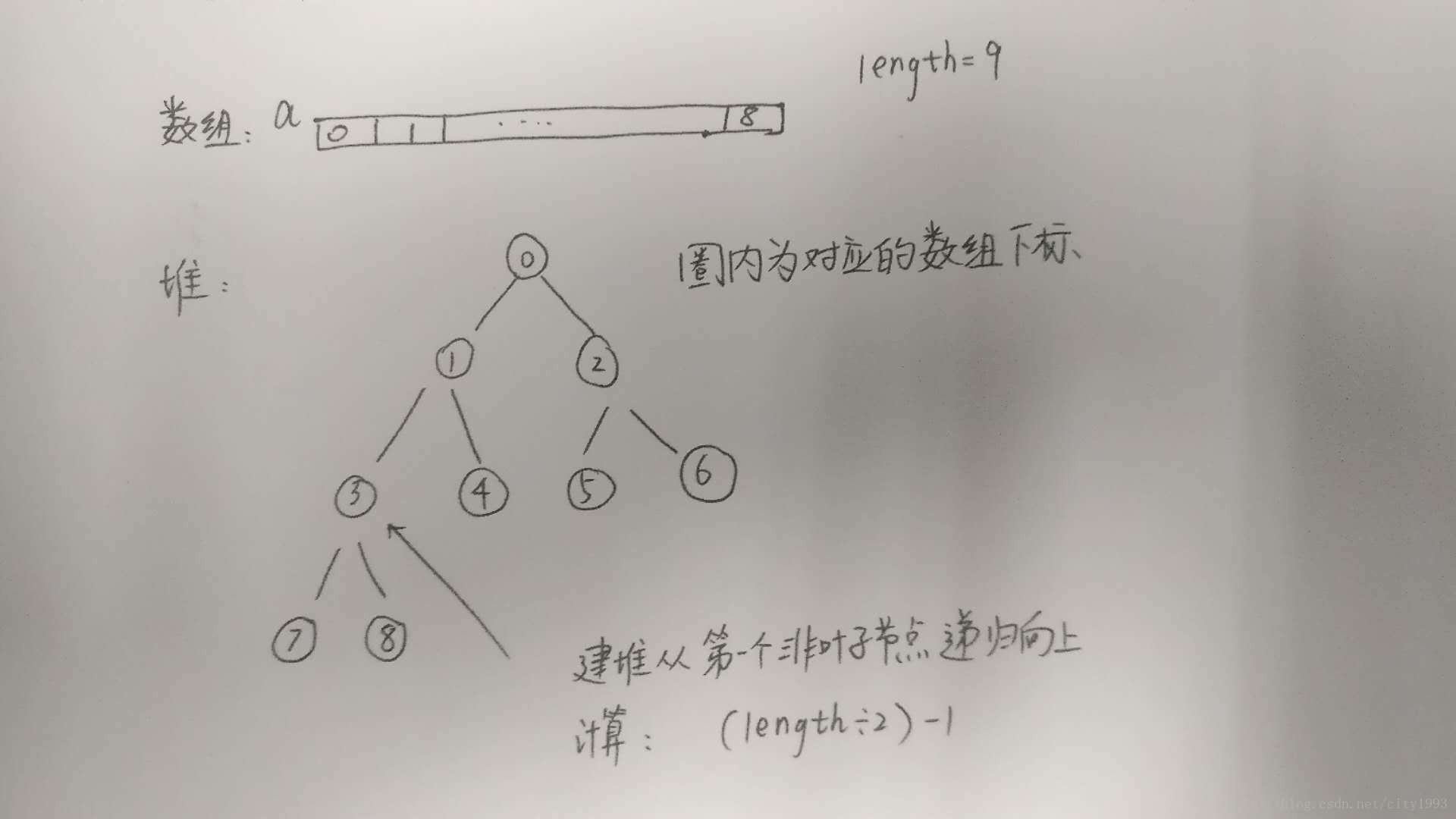
堆排序將要排序的物件看做一顆完全二叉樹，資料結構可以用陣列來實現。

 初始化建堆過程時間：O(n)                                    更改堆元素後重建堆時間：O(nlogn)                                                                         

具體證明可見：http://blog.csdn.net/yuzhihui_no1/article/details/44258297

下面的做法是在建好堆之後，交換堆頂和堆底之後，又執行了重建堆的過程。複雜度應該為O(n^2)。

待比較程式程式碼如下:

package ex;
import java.util.Arrays;

public class Sort {
    public static void main(String args[]) {  
        int []a = new int[] {16,25,34,27,30,5,7,4,41,55};
        Sort.heapSort(a);
        System.out.println(Arrays.toString(a));
    }
    static
 
 int parent(int i) {
        return (i - 1)/2;
    }
    static int left(int i) {
        return 2*i + 1;
    }
    static int right(int i) {
        return 2*i + 2;
    }
    static void maxHeapfy(int []a,int i,int heapSize) {   //陣列a，第i個結點，heapSize是陣列種實際要排序的元素的長度
        int left = left(i);     //有的時候能夠遞迴到葉子結點，葉子結點無後繼，下面兩個if都注意到了這一點
 

        int right = right(i);   
        int largest = i;
        if(left < heapSize && a[left] > a[largest]) {   //
            largest = left;
        }
        if(right < heapSize && a[right] > a[largest])  
        {
            largest = right;
        }
        if(largest != i) {      //把最大值給父結點
            a[largest] = a[largest] ^ a[i];
            a[i] = a[largest] ^ a[i];
            a[largest] = a[largest] ^ a[i];
            maxHeapfy(a,largest,heapSize);    //發生交換之後還要保證大根堆性質
        }
    }
    static void buildMaxHeap(int []a,int heapSize) {
        for(int i = (heapSize-1)/2;i >= 0;i--) {  //此處計算非葉子節點時和計算父節點混淆
            maxHeapfy(a,i,heapSize);              //此處呼叫重建堆的過程增加了時間複雜度
        }
    }
    staticvoid heapSort(int []a) {
        for(int i = a.length-1;i > 0;i--) {
            buildMaxHeap(a,i+1);   //堆的大小從n到2
            a[i] = a[0] ^ a[i];    //交換
            a[0] = a[0] ^ a[i];
            a[i] = a[0] ^ a[i];
        }
    }
}
//輸出結果://[4, 5, 7, 16, 25, 27, 30, 34, 41, 55]

改進的重建堆的過程

public class HeapSorter implements Sorter{

	/* (non-Javadoc)
	 * @see A4.Sorter#sort(java.lang.Comparable[])
	 */
	@Override
	public void sort(Comparable[] data) {
		buildMaxHeap(data,data.length);
	}
	
	int parent(int i)
	{
		return (i-1)/2;
	}
	
	int left(int i)
	{
		return 2*i+1;
	}
	
	int right(int i)
	{
		return 2*i+2;
	}
	
	/**
	 * 將堆排序選出的最大的元素放到陣列的最後位置。
	 * 下午10:38:26
	 * 2017年11月29日
	 * @author city
	 */
	private void buildMaxHeap(Comparable[] data, int heapSize) {
		// First Step build Max-heap
		for(int i = heapSize/2-1;i>=0;i--) 
		{
			maxHeapfy(data,i,heapSize);
		}
			
		for(int i = data.length-1;i>0;i--)
		{
			Comparable tmp = data[i];
			data[i] = data[0];
			data[0] = tmp;
			maxHeapfy(data, 0, i);
		}

	}
	
	/**
	 * 堆排序演算法核心，建立最大堆。
	 * 下午10:39:54
	 * 2017年11月29日
	 * @author city
	 */
	private void maxHeapfy(Comparable[] data, int i, int heapSize) {
		// TODO Auto-generated method stub
		int left = left(i);
		int right = right(i);
		int largest = i;
		if(left<heapSize && data[left].compareTo(data[largest])>0)
		{
			largest = left;
		}
		if(right<heapSize && data[right].compareTo(data[largest])>0)
		{
			largest = right;
		}
		if(largest!=i)
		{
			Comparable tmp = data[largest];
			data[largest] = data[i];
			data[i] = tmp;
			maxHeapfy(data, largest, heapSize);
		}
		
	}	
}

比較原文轉載自http://blog.csdn.net/qq_35178267/article/details/78313306#insertcode

如有侵權請聯絡