在數字影象中，往往存在著一些特殊形狀的幾何圖形，像檢測馬路邊一條直線，檢測人眼的圓形等等，有時我們需要把這些特定圖形檢測出來，hough變換就是這樣一種檢測的工具。

Hough變換的原理是將特定圖形上的點變換到一組引數空間上，根據引數空間點的累計結果找到一個極大值對應的解，那麼這個解就對應著要尋找的幾何形狀的引數（比如說直線，那麼就會得到直線的斜率k與常熟b，圓就會得到圓心與半徑等等）。

關於hough變換，核心以及難點就是關於就是有原始空間到引數空間的變換上。以直線檢測為例，假設有一條直線L，原點到該直線的垂直距離為p，垂線與x軸夾角為θ，那麼這條直線是唯一的，且直線的方程為 ρ=xco

sθ+ysinθ, 如下圖所示：

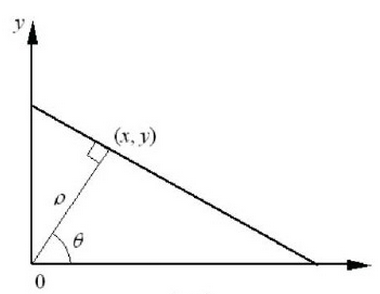
可以看到的是這條直線在極座標系下只有一個(ρ,θ)與之對應，隨便改變其中一個引數的大小，變換到空間域上的這個直線將會改變。好了，再回來看看這個空間域上的這條直線上的所有點吧，你會發現，這條直線上的所有點都可以是在極座標為(ρ,θ)所表示的直線上的，為什麼說是都可以在，因為其中隨便的一個點也可以在其他的(ρ,θ)所表示的直線上，就比如上述的(x,y)吧，它可以再很多直線上，準確的說，在經過這個點的直線上，隨便畫兩條如下：

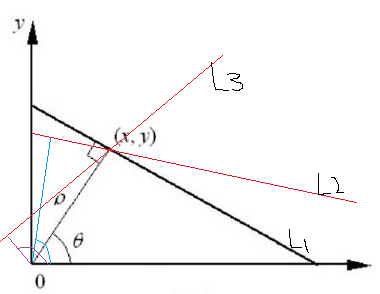
可以看到，光是空間上的一個點在極座標系下就可能在很多極座標對所對應的直線上，具體有多少個極座標對呢？那得看你的θ的步長了，我們可以看到θ

無非是從0-360度（0−2π）變化，假設我們沒10度一走取一個直線（這個點在這個直線上），那麼我們走一圈是不是取了36條直線，也就對應36個極座標對沒錯吧，那麼這個極座標對，畫在座標軸上是什麼樣子的呢？因為θ是從0−2π，並且一個點定了，如果一個θ也定了，你想想它對應的直線的ρ會怎麼樣，自然也是唯一的。那麼這個點在極座標下對應的(ρ,θ)畫出來一個週期可能就是這樣的，以θ為x軸的話：

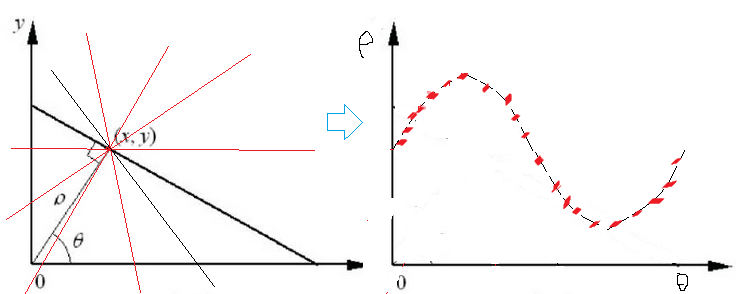
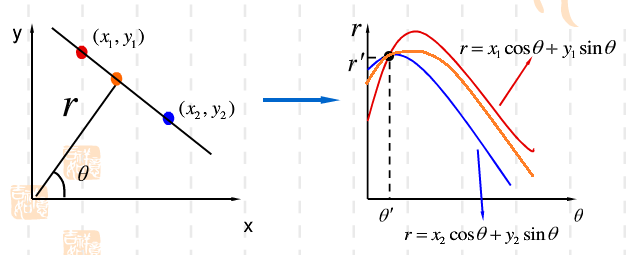
ok前面說的是單單這一個點對應的極座標系下的引數對，那麼如果每個點都這麼找一圈呢？也就是每個點在引數空間上都對應一系列引數對吧，現在把它們華仔同一個座標系下會怎麼樣呢？為了方便，假設在這個直線上取3個點畫一下：

那麼可以看到，首先對於每一個點，在極座標下，會存在一個週期的曲線來表示通過這個點，其次，這三個極座標曲線同時經過一個點，要搞清楚的是，極座標上每一個點對(ρ,θ)在空間座標上都是對應一條直線的。好了，同時經過的這一個點有什麼含義呢？它表示在空間座標系下，有一條直線可以經過點1，經過點2，經過點3，這是什麼意思？說明這三個點在一條直線上吧。反過來再來看這個極座標系下的曲線，那麼我們只需要找到交點最多的點，把它返回到空間域就是這個需要找的直線了。為什麼是找相交最多的點，因為上面這只是三個點的曲線，當空間上很多點都畫出來的時候，那麼相交的點可能就不知上述看到的一個點了，可能有多個曲線相交點，但是有一點，勢必是一條直線上的所有點匯成的交點是曲線相交次數最多的。

再來分析這個演算法。可以看到hough變換就是引數對映變換。對每一個點都進行對映，並且每一個對映還不止一次，(ρ,θ)都是存在步長的，像一個點對映成一個(ρ,θ)，以θ取步長為例，當θ取得步長大的時候，對映的(ρ,θ)對少些，反之則多，但是我們有看到，對映後的點對是需要求交點的，上述畫出來的曲線是連續的，然而實際上因為θ步長的存在，他不可能是連續的，像上上個圖一樣，是離散的。那麼當θ步長取得比較大的時候，你還想有很多交點是不可能的，因為這個時候是離散的曲線然後再去相交，所以說θ步長不能太大，理論上是越小效果越好，因為越小，越接近於連續曲線，也就越容易相交，但是越小帶來的問題就是需要非常多的記憶體，計算機不會有那麼多記憶體給你的，並且越小，計算量越大，想想一個點就需要對映那麼多次，每次對映是需要計算的，耗時的。那麼再想想對於一副影象所有點都進行對映，隨便假設一副100*100的影象（很小吧），就有10000個點，對每個點假設就對映36組(ρ,θ)引數（此時角度的步長是10度了，10度，已經非常大的一個概念了），那麼總共需要對映360000次，在考慮每次對映計算的時間吧。可想而知，hough是多麼耗時耗力。所以必須對其進行改進。首先就是對影象進行改進，100*100的影象，10000個點，是不是每個點都要計算？大可不必，我們只需要在開始把影象進行一個輪廓提取，一般使用canny運算元就可以，生成黑白二值影象，白的是輪廓，那麼在對映的時候，只需要把輪廓上的點進行引數空間變換，為什麼提輪廓？想想無論檢測影象中存在的直線呀圓呀，它們都是輪廓鮮明的。那麼需要變換的點可能就從10000個點降到可能1000個點了，這也就是為什麼看到許多hough變換提取形狀時為什麼要把影象提取輪廓，變成二值影象了。

繼續演算法，分析這麼多，可想而知那麼一個hough變換在演算法設計上就可以如下步驟：
（1）將引數空間(ρ,θ)量化，賦初值一個二維矩陣M，M(ρ,θ)就是一個累加器了。
（2）然後對影象邊界上的每一個點進行變換，變換到屬於哪一組(ρ,θ)，就把該組(ρ,θ)對應的累加器數加1，這裡的需要變換的點就是上面說的經過邊緣提取以後的影象了。
（3）當所有點處理完成後，就來分析得到的M(ρ,θ)，設定一個閾值T，認為當M(ρ,θ)>T，就認為存在一條有意義的直線存在。而對應的M(ρ,θ)就是這組直線的引數，至於T是多少，自己去式，試的比較合適為止。
（4）有了M(ρ,θ)和點（x,y）計算出來這個直線就ok了。

說了這麼多，這就是原理上hough變換的最底層原理，事實上完全可以自己寫程式去實現這些，然而，也說過，hough變換是一個耗時耗力的演算法，自己寫迴圈實現通常很慢，曾經用matlab寫過這個，也有實際的hough變換例子可以看看：

那麼我們在實際中大可不必自己寫，opencv已經集成了hough變換的函式，呼叫它的函式效率高，也很簡單。
Opencv中檢測直線的函式有cv2.HoughLines()，cv2.HoughLinesP()
函式cv2.HoughLines()返回值有三個（opencv 3.0），實際是個二維矩陣，表述的就是上述的(ρ,θ)，其中ρ的單位是畫素長度（也就是直線到影象原點(0,0)點的距離），而θ的單位是弧度。這個函式有四個輸入，第一個是二值影象，上述的canny變換後的影象，二三引數分別是ρ和θ的精確度，可以理解為步長。第四個引數為閾值T，認為當累加器中的值高於T是才認為是一條直線。自己畫了個圖實驗一下：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('line.jpg') 
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度影象 
#open to see how to use: cv2.Canny
#http://blog.csdn.net/on2way/article/details/46851451 
edges = cv2.Canny(gray,50,200)
plt.subplot(121),plt.imshow(edges,'gray')
plt.xticks([]),plt.yticks([])
#hough transform
lines = cv2.HoughLines(edges,1,np.pi/180,160)
lines1 = lines[:,0,:]#提取為為二維
for rho,theta in lines1[:]: 
a = np.cos(theta)
b = np.sin(theta)
x0 = a*rho
y0 = b*rho
x1 = int(x0 + 1000*(-b))
y1 = int(y0 + 1000*(a))
x2 = int(x0 - 1000*(-b))
y2 = int(y0 - 1000*(a)) 
cv2.line(img,(x1,y1),(x2,y2),(255,0,0),1)

plt.subplot(122),plt.imshow(img,)
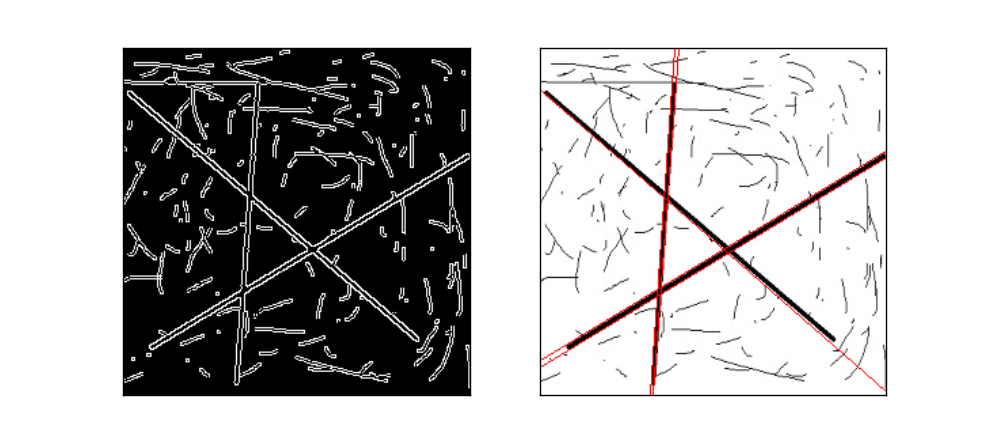
plt.xticks([]),plt.yticks([])

測試一個新的圖，不停的改變 cv2.HoughLines最後一個閾值引數到合理的時候如下：

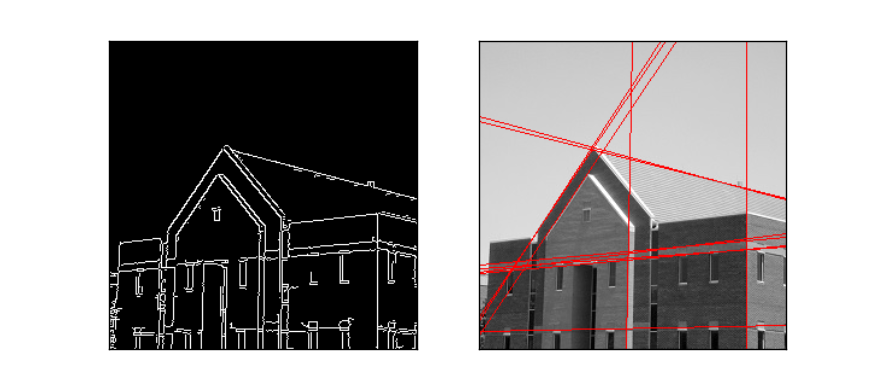
可以看到檢測的還可以的。

函式cv2.HoughLinesP()是一種概率直線檢測，我們知道，原理上講hough變換是一個耗時耗力的演算法，尤其是每一個點計算，即使經過了canny轉換了有的時候點的個數依然是龐大的，這個時候我們採取一種概率挑選機制，不是所有的點都計算，而是隨機的選取一些個點來計算，相當於降取樣了。這樣的話我們的閾值設定上也要降低一些。在引數輸入輸出上，輸入不過多了兩個引數：minLineLengh(線的最短長度，比這個短的都被忽略)和MaxLineCap（兩條直線之間的最大間隔，小於此值，認為是一條直線）。輸出上也變了，不再是直線引數的，這個函式輸出的直接就是直線點的座標位置，這樣可以省去一系列for迴圈中的由引數空間到影象的實際座標點的轉換。

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('room.jpg') 
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度影象 
#open to see how to use: cv2.Canny
#http://blog.csdn.net/on2way/article/details/46851451 
edges = cv2.Canny(gray,50,200)
plt.subplot(121),plt.imshow(edges,'gray')
plt.xticks([]),plt.yticks([])
#hough transform
lines = cv2.HoughLinesP(edges,1,np.pi/180,30,minLineLength=60,maxLineGap=10)
lines1 = lines[:,0,:]#提取為二維
for x1,y1,x2,y2 in lines1[:]: 
    cv2.line(img,(x1,y1),(x2,y2),(255,0,0),1)

plt.subplot(122),plt.imshow(img,)
plt.xticks([]),plt.yticks([])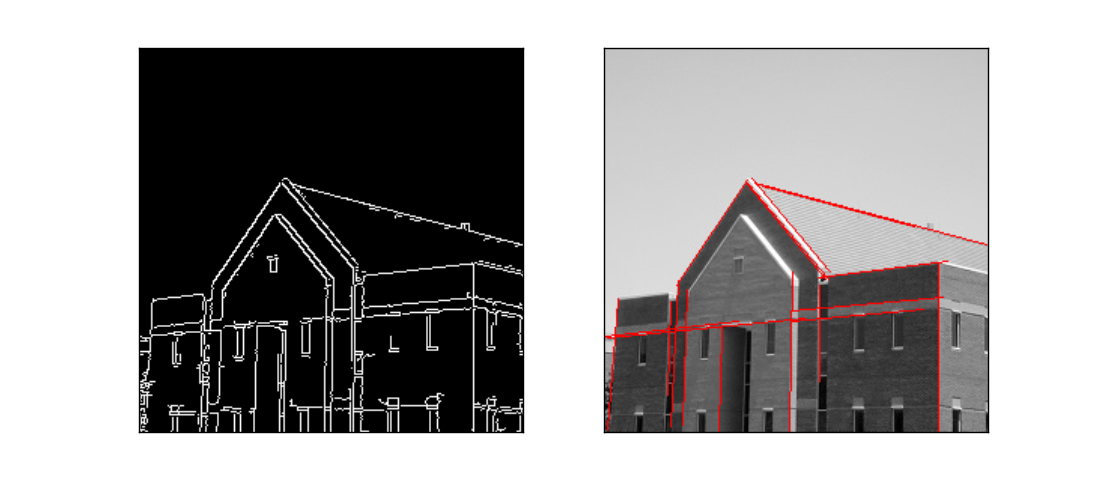

可以看到這個方法似乎更好些，速度還快，調引數得到較好的效果就ok了。

Ok說完了直線的檢測，再來說說圓環的檢測，我們知道圓的數學表示為：

(x−xcenter)2+(y−ycenter)2=r2
從而一個圓的確定需要三個引數，那麼就需要三層迴圈來實現（比直線的多一層），從容把影象上的所有點對映到三維引數空間上。其他的就一樣了，尋找引數空間累加器的最大（或者大於某一閾值）的值。那麼理論上圓的檢測將比直線更耗時，然而opencv對其進行了優化，用了一種霍夫梯度法，感興趣去研究吧，我們只要知道它能優化演算法的效率就可以了。關於函式引數輸入輸出：
cv2.HoughCircles(image, method, dp, minDist, circles, param1, param2, minRadius, maxRadius)
這個時候輸入為灰度影象，同時最好規定檢測的圓的最大最小半徑，不能盲目的檢測，否側浪費時間空間。輸出就是三個引數空間矩陣。
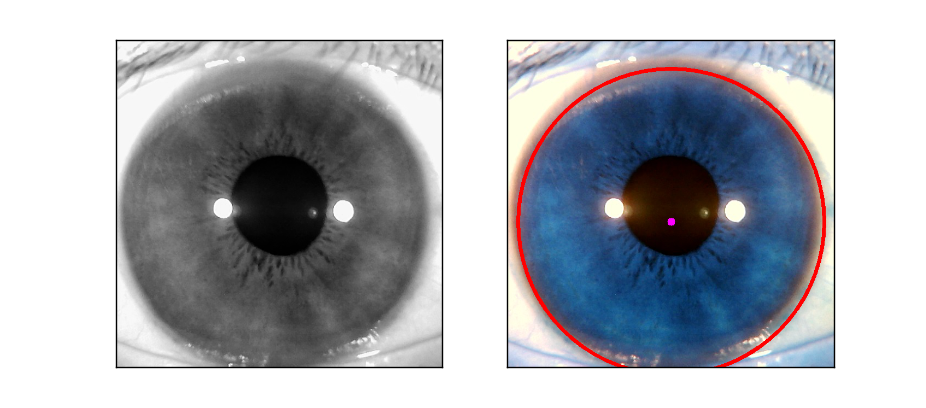
來個實際點的人眼影象，把minRadius和maxRadius調到大圓範圍檢測如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('eye.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度影象 

plt.subplot(121),plt.imshow(gray,'gray')
plt.xticks([]),plt.yticks([])
#hough transform
circles1 = cv2.HoughCircles(gray,cv2.HOUGH_GRADIENT,1,
100,param1=100,param2=30,minRadius=200,maxRadius=300)
circles = circles1[0,:,:]#提取為二維
circles = np.uint16(np.around(circles))#四捨五入，取整
for i in circles[:]: 
    cv2.circle(img,(i[0],i[1]),i[2],(255,0,0),5)#畫圓
    cv2.circle(img,(i[0],i[1]),2,(255,0,255),10)#畫圓心

plt.subplot(122),plt.imshow(img)
plt.xticks([]),plt.yticks([])

把半徑範圍調小點，檢測內圓：

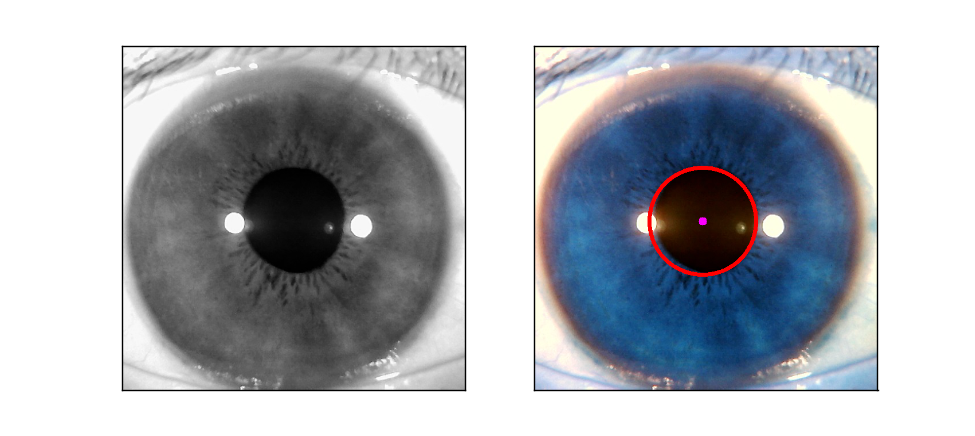
至此圓的檢測就是這樣。