定義：它的基本思想是：通過一趟排序將要排序的資料分割成獨立的兩部分，其中一部分的所有資料都比另外一部分的所有資料都要小，然後再按此方法對這兩部分資料分別進行快速排序，整個排序過程可以遞迴進行，以此達到整個資料變成有序序列。

過程：

用自己的話： 以前大學的時候聽說牛逼的程式設計師是能裸寫快排，導致自己學習快速排序的時候帶有一點點壓力，也有點難以理解，不過當我看到這篇 快速排序白話文的時候，在紙上面演示了幾下，便豁然開朗，coding了一下，對作者的“挖坑填數”思想更加了解深刻，判斷過程如下：

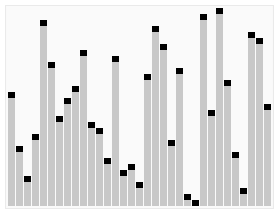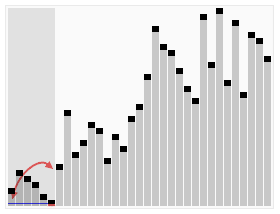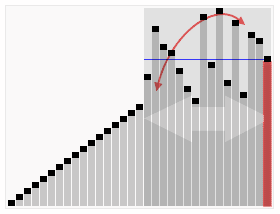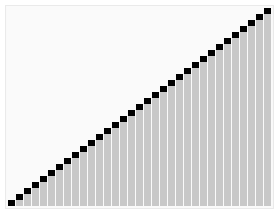
以一個數組作為示例，取區間第一個數57為基準數，也就是第一張動圖的基準線。
初始時，i = 0
 
;  j = 9;   X = a[i] = 57
由於已經將a[0]中的數儲存到X中，可以理解成在陣列a[0]上挖了個坑，可以將其它資料填充到這來。
從j開始向前找一個比X小或等於X的數。當j=9，符合條件，將a[9]挖出再填到上一個坑a[0]中。a[0]=a[8]; i++;  這樣一個坑a[0]就被搞定了，但又形成了一個新坑a[9]，這怎麼辦了？簡單，再找數字來填a[9]這個坑。這次從i開始向後找一個大於X的數，當i=1，符合條件，將a[1]挖出再填到上一個坑中a[9]=a[1]; j--。這樣就進行了一次遍歷。

第二次開始i = 1;   j = 8;   X=57
再重複上面的步驟，先從後向前找，再從前向後找。
....

從i開始向後找，當i=5
 
時，由於i==j退出。

此時，i = j = 5，而a[5]剛好又是上次挖的坑，因此將X填入a[5]。

可以看出a[5]前面的數字都小於它，a[5]後面的數字都大於它。因此再對a[0…4]和a[6…9]這二個子區間重複上述步驟就可以了。

對挖坑填數進行總結
- 1．i =L; j = R; 將基準數挖出形成第一個坑a[i]。
- 2．j–由後向前找比它小的數，找到後挖出此數填前一個坑a[i]中。
- 3．i++由前向後找比它大的數，找到後也挖出此數填到前一個坑a[j]中。
- 4．再重複執行2，3二步，直到i==j，將基準數填入a[i]中。

程式碼：

    public
 
 int[] quickSort(int[] a, int l, int r) {
        if (l < r) {
            int i = l, j = r, v = a[l];//i:左邊開始活動座標，j:右邊開始活動座標，v：基數，用於對比的值，一般取第一個
            while (i < j) {//只要左邊遊標和遊標不重疊的話那麼就繼續遍歷
                //每一輪遍歷的時候只進行一輪，把右邊的一個比基數小的數移動到左邊，把左邊比基數大的數移動到右邊
                while (i < j && a[j] > v) 
                    // 找出右邊比左邊小的座標
                    j--;
                if (i < j)
                    a[i++] = a[j];//進行移動，左邊座標移動一個數
                while (i < j && a[i] < v)
                    // 找出左邊比右邊大的左邊
                    i++;
                if (i < j)
                    a[j--] = a[i];//進行移動，右邊座標移動一個數
            }
            a[i] = v;//當遊標重疊時填入基數
            this.quickSort(a, l, i - 1);
            this.quickSort(a, i + 1, r);
            return a;
        }
        return a;
    }

演算法複雜度：