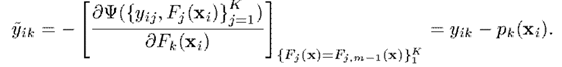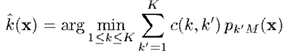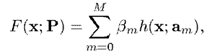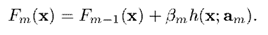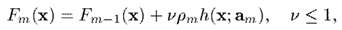GBDT梯度提升樹演算法原理小結(三)
首先我們回顧一下Gradient Boosting 的本質,就是訓練出,使損失函式最小,即
其求解步驟如下:
所以,我們首先得定義出損失函式,才能談求解的事情。接下來我們針對不同場景,介紹相應的損失函式。
迴歸
對於迴歸問題,定義好損失函式後,Gradient Boosting 不需要作出什麼修改,計算出來的結果就是預測值。
平方損失
在實際迴歸中,最常用的之一,就是平方損失,即
將它畫出來,形狀大致如下
能看出來,它含義就是對較大的偏差有著很強的懲罰,並相對忽略較小的偏差。容易得到,的梯度為
因此代入Algorithm 1,就有了將平方損失應用於Gradient Boosting 的 LS_Boost 方法,步驟如下
絕對值損失
絕對值損失的定義,以及其梯度如下:
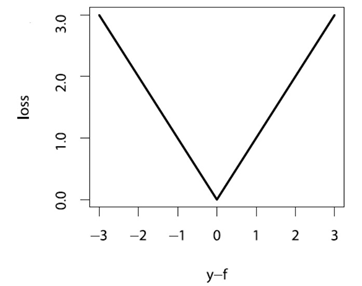
絕對值損失函式畫出來圖,形狀如下
有了以上兩項(損失函式與梯度),本質上就能夠解Algorithm 1了。同時,如果將弱學習演算法設為決策樹,還能進一步推匯出形式更簡潔的演算法形式。這部分公式推導,此處不再贅述,有興趣的同學可以參看原文。絕對值損失的 GBDT 演算法流程如下
需要了解的是,使用絕對值損失,一般比平方損失更加穩健。
Huber 損失
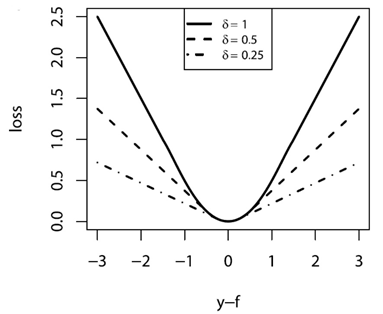
還有一種叫Huber 損失,其定義為
分段函式看起來不直觀,它的圖畫出來大致是
從圖和公式可以看出,它融合了平方損失和絕對值損失。當偏差較小時,採用平方差損失;當偏差較大時,採用絕對值損失;而引數
按照作者的說法,對於正態分佈的資料,Huber 損失的效果近似於平方差損失;而對於長尾資料,Huber 損失的效果近似於絕對值損失;而對於中等程度拖尾的資料,Huber 損失的效果要優於以上兩者。
與平方差損失一樣,如果將弱學習演算法設為決策樹,還能進一步推匯出更具體的演算法形式,即,Huber 損失的 GBDT 演算法流程如下
三種損失函式與對應的梯度表
分類
在說明分類之前,我們先介紹一種損失函式。與常見的直接求預測與真實值的偏差不同,這種損失函式的目的是最大化預測值為真實值的概率。這種損失函式叫做對數損失函式(Log-Likehood Loss),定義如下
對於二項分佈,,我們定義預測概率為,即二項分佈的概率,可得
即,可以合併寫成
對於與的關係,我們定義為
即,。當,;當,
兩類分類
對於兩類分類,,我們先將它轉成二項分佈,即令。
於是根據上面得到的,損失函式期望為
其中,定義為
接下來求出梯度
這樣,Gradient Boosting 需要的條件就準備齊了。
但是,如果我們將弱演算法設定為決策樹,並在求解步長的時候利用牛頓法,原演算法能夠得到如下更簡潔的形式,即兩類分類的 GBDT 演算法流程如下
最後依據計算出來的分類即可。即,通過估算預測的概率
然後根據以下準則預測標籤,其中是代價函式,表示當真實類別為,預測類別為時的代價
多類分類
模仿上面兩類分類的損失函式,我們能夠將類分類的損失函式定義為
其中,,且將與關係定義為
或者,換一種表達方式
接下來求出梯度
於是可以看出,這裡在每一次迭代,都要求個引數,和對應的。而求出的則可以理解為屬於第類而不是其他類的概率。本質上就是OneVsRest的思想。
同上,如果我們對弱演算法選擇決策樹,則有類分類的 GBDT 演算法流程為
然後,根據上面的公式,將最終得到的轉換為對應的類別概率,並用於分類即可。分類準則如下
其中,是代價函式,表示當真實類別為,預測類別為時的代價
正則化
採取以上演算法去訓練測試樣本集,能很好地擬合測試資料,相對不可避免地會產生過擬合。為了減少過擬合,可以從兩個方面入手,即弱演算法的個數,以及收縮率。
弱演算法的個數
在推導 AdaBoost 的時候,我們就介紹過,我們希望訓練出的是若干個弱演算法的線性組合,即
因此,這個的大小就影響著演算法的複雜度。
一般來說,在訓練階段,我們通過交叉驗證的方式,選擇使損失最小的,並用於測試。
收縮率
前面介紹過,在第次迭代時,我們用如下公式更新
而增加收縮率後,則更新公式變為
即越往後訓練出的弱演算法,其在總演算法中佔得權重相對越低,於是真正有效的弱演算法也就前面有限個,因而影響了演算法的複雜度。
同樣,在訓練階段,我們通過交叉驗證的方式,選擇使損失最小的,並用於測試。
不過,和是會相互影響的,一般減小,則對應的最優的會增加。因此,在選擇引數時,應該綜合考慮這兩個引數的效果。
尾巴
在這一部分,我們看到不論在分類還是迴歸的Gradient Boosting,如果弱演算法選擇決策樹,都能夠一定程度簡化求解思路;同時,決策樹是個簡單容易實現的弱演算法,在實際中 GBDT 的表現也很好,相反太強太穩定的演算法反而容易過擬合。希望這兩篇文章不僅能幫助大家瞭解 GBDT 這類演算法,更多的是能瞭解它整個演化的過程,對它有個更深的理解。

 所以,我們首先得定義出損失函式
所以,我們首先得定義出損失函式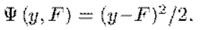
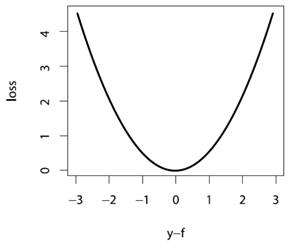 能看出來,它含義就是對較大的偏差有著很強的懲罰,並相對忽略較小的偏差。容易得到,
能看出來,它含義就是對較大的偏差有著很強的懲罰,並相對忽略較小的偏差。容易得到,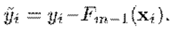 因此代入Algorithm 1,就有了將平方損失應用於Gradient Boosting 的 LS_Boost 方法,步驟如下
因此代入Algorithm 1,就有了將平方損失應用於Gradient Boosting 的 LS_Boost 方法,步驟如下
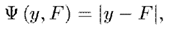
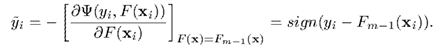

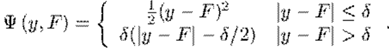


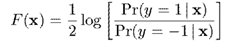
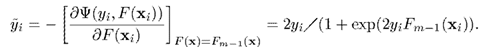

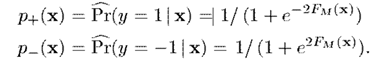
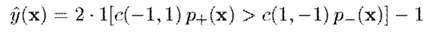
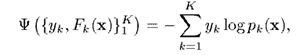
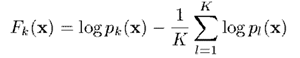
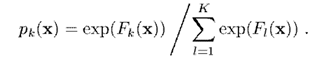 接下來求出梯度
接下來求出梯度