關於演算法競賽入門經典一書的思考學習——列舉排序和子集生成!
一、生成1~n的排列:
這程式碼的實現使用了遞迴的方式!唉,但是關於遞迴的使用還是不夠熟練,理解亦不夠深入,顧作此文!
還有就是從演算法到程式的實現,覺得還是欠缺很多啊!
/* Date:2014/11/02 By: VID Function: 在本程式中實現了兩個功能。 1、 輸入正整數n,按字典序從小到大的順序輸出1~n的所有排列。列如: Sample Input 3 Sample Output 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 2、手動錄入陣列(輸入的沒有重複元素!!),按字典序從小到大的順序輸出該陣列的所有排列。(程式中所有標註方式2的。)列如: Sample Input 3 2 4 6 Sample Output 2 4 6 2 6 4 4 2 6 4 6 2 6 2 4 6 4 2 */ #include<iostream> using namespace std; #define N 500 int P[N],A[N]; // 遞迴… void print_pumutation(int n,int* A,int cur) { int i,j; if(cur == n) // cur指的是當前的位置! { for(i = 0;i<n;i++) cout<<A[i]; cout<<endl; } else for(i = 1;i<=n;i++)// 若為方式2:就要修改為:for(i = 0;i<n;i++) { int ok = 1; for(j = 0;j<cur;j++) if(A[j] == i) ok = 0; // 方式2: if(A[j] == P[i]) ok = 0; if(ok) { A[cur] = i; //方式2: A[cur] = P[i]; print_pumutation(n,A,cur+1); } } } int main() { int n; while(cin>>n) { /* 方式2: for(int i = 0;i<n;i++) { cin>>P[i]; } */ memset(A,0,sizeof(A)); print_pumutation(n,A,0); } return 0; }
二、生成可重集的排列
注:這裡的意思是輸入中有重複元素,我們輸出的各個排列當然是不會重複的。
例如:Sample Input
3
1 1 2
Sample Output
1 1 2
1 2 1
2 1 1
對於這樣的問題:
/* Date:2014/11/02 By: VID Attention: 對於這樣的問題,只需在上一個程式的基礎之上做一些修改, 便可得到輸入是重複集的全排列。 ->如果想用字典序輸出,只需加上一個排序的函式即可。 */ #include<iostream> using namespace std; #define N 500 int P[N],A[N]; // 遞迴… void print_pumutation(int n,int P[],int* A,int cur) { int i,j; if(cur == n) // cur指的是當前的位置! { for(i = 0;i<n;i++) cout<<A[i]; cout<<endl; } else for(i = 0;i<n;i++) if(!i||P[i]!=P[i-1]) // 這裡是為了檢查P的第一個元素和所有與第一個元素不相同的元素, // 只有這個時候,我們才對它進行遞迴呼叫! { int c1 = 0,c2 = 0; for(j = 0;j<cur;j++) if(A[j] == P[i]) c1++; // 在A[0]~A[cur-1]中P[i]出現的次數。 for(j = 0;j<n;j++) if(P[i] == P[j]) c2++; // 在陣列P中P[i]出現的次數。 if(c1<c2) { A[cur] = P[i]; print_pumutation(n,P,A,cur+1); } } } int main() { int n; while(cin>>n) { for(int i = 0;i<n;i++) { cin>>P[i]; } memset(A,0,sizeof(A)); print_pumutation(n,P,A,0); } return 0; }
(2)與上面的剛剛相反,下面的程式輸出的每一個排列之中的元素是可以重複的,而元素輸入是不能有重複的。
例如:Sample Input
2
1 2
Sample Output
1 1
1 2
2 1
/* Date:2014/11/02 By: VID Function: 使用規則:要求輸入的元素沒有重複元素。 結果 :輸出有重複元素的全排列!! */ #include<iostream> using namespace std; #define N 500 int P[N],A[N]; void print_pumutation(int n,int* A,int cur) { int i,j; if(cur == n) // cur指的是當前的位置! { for(i = 0;i<n;i++) cout<<A[i]; cout<<endl; } else for(i = 0;i<n;i++) { A[cur] = P[i]; print_pumutation(n,A,cur+1); } } int main() { int n; while(cin>>n) { for(int i = 0;i<n;i++) { cin>>P[i]; } memset(A,0,sizeof(A)); print_pumutation(n,A,0); } return 0; }
關於剛剛上面研究的兩個問題,還可以使用STL中的庫函式next_permutation(生成下一個全排列!)。這個函式可以輕鬆的解決上面的兩個問題。下面舉個例子,這個例子來自:點選開啟連結
/*
對於這些"lcq", "love", "code", "plmm"字串按照字典序把他們的全排列輸出來。
所以當然,對於字串都可以輸出他們的排列,簡單的整形陣列就更不在話下,可以很出色的解決
他們的全排列,無論輸入是否有重複。
*/
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main()
{
string word[] = {"lcq", "love", "code", "plmm"};//C++裡面帶的一個string類
int n = sizeof(word) / sizeof(word[0]);
sort(word, word+n);//排序
do
{
for(int i=0; i<n; ++i)
cout<<word[i]<<" ";
cout<<endl;
}while(next_permutation(word, word+n));
return 0;
}
/***Output********
code lcq love plmm
code lcq plmm love
code love lcq plmm
code love plmm lcq
code plmm lcq love
code plmm love lcq
lcq code love plmm
lcq code plmm love
lcq love code plmm
lcq love plmm code
lcq plmm code love
lcq plmm love code
love code lcq plmm
love code plmm lcq
love lcq code plmm
love lcq plmm code
love plmm code lcq
love plmm lcq code
plmm code lcq love
plmm code love lcq
plmm lcq code love
plmm lcq love code
plmm love code lcq
plmm love lcq code
******************/->接下來是這個神奇的函式:next_permutation的函式內部實現過程(當然也有prev_permutation)。見程式碼:
#include<iostream>
#include<algorithm>
using namespace std;
template<class BidirectionalIterator>
bool my_next_permutation(BidirectionalIterator first, BidirectionalIterator last)
{
if(first == last)//空區間
return false;
BidirectionalIterator i = first;
if(last == ++i)//只有一個元素
return false;
i = last;//i 指向尾端
--i;
for(;;)
{
BidirectionalIterator ii = i;
--i;
if(*i < *ii)//如果前一個元素小於後一個元素
{
BidirectionalIterator j = last;//令j指向尾端
while(!(*i < *--j));//有尾端往前棧、直到遇上比 *i大的元素
iter_swap(i, j);//交換i,j
reverse(ii, last);//將ii之後的元素全部逆向重排
return true;
}
if(i == first)//進行至最前面了
{
reverse(first, last);//全部逆向重排
return false;
}
}
}
int main()
{
char a[] = {'d', 'c', 'a', 'a'};
int n = sizeof(a) / sizeof(a[0]);
sort(a, a+n);
do
{
for(int i=0; i<n; ++i)
cout<<a[i]<<" ";
cout<<endl;
}while(my_next_permutation(a, a+n));
return 0;
}Description
從集合{1,2,3,...,n}中選取k個數所組成的所有集和。
Input
輸入的兩個正整數。第一個數為n(1<=n<=20),第二個數為k,(k<=n),兩個數之間用空格隔開。
Output
輸出含有k個數的所有不相同的集合,輸出集合的序列按照字典序輸出,每個集合佔一行,集合的相鄰兩個數字用空格隔開。
Sample Input
3 2
Sample Output
1 2
1 3
2 3
(1)、增量構造法:即:一次選出一個元素放到集合中。
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
using namespace std;
const int MAX = 100;
int cmp(const void *a, const void *b)
{
return *(int*)a - *(int*)b;
}
void fullCombination(int num[], int rcd[], int cur, int begin, int n)
{
int i;
for(i=0; i<cur; ++i)
printf("%d ", rcd[i]);
printf("\n");
for(i=begin; i<n; ++i)
{
rcd[cur] = num[i];
fullCombination(num, rcd, cur+1, i+1, n);
}
}
int main()
{
int num[MAX], rcd[MAX], i, n,a;
cin>>n;
while(1)
{
for(i=0; i<n; ++i)
{
cin>>a;
num[i] = a;
}
qsort(num, n, sizeof(num[0]), cmp);
fullCombination(num, rcd, 0, 0, n);
}
return 0;
}
/*
INPUT
3
3 2 1
OUTPUT
1
1 2
1 2 3
1 3
2
2 3
3
*/
很顯然,遞迴的邊界是集合num[]中沒有數的時候。
(2)、位向量法:
第二種方法是構造一個位向量B[i],其中當B[i]==1的時候i元素在子集a[]中,B[i]==0時不在子集a[]中。程式碼如下:
#include<stdio.h>
const int MAX = 100;
void fullCombination(int n, int* B, int cur)
{
if(cur == n)
{
for(int i = 0; i < cur; i++)
{
if(B[i])
printf("%d ", i+1); // 列印當前集合
}
printf("/n");
return;
}
B[cur] = 1; // 選第cur個元素
fullCombination(n, B, cur+1);
B[cur] = 0; // 不選第cur個元素
fullCombination(n, B, cur+1);
}
int main()
{
int B[MAX], n;
while(scanf("%d", &n) != EOF)
fullCombination(n, B, 0);
return 0;
}
/*
INPUT
3
OUTPUT
1 2 3
1 2
1 3
1
2 3
2
3
*/
(三)、二進位制法
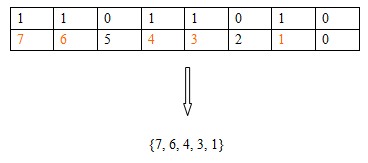
接下來我要重點介紹的一種方法是利用二進位制來表示{1,2,3,……,}的子集S:從右往左用一個整數的二進位制表示元素i是不是再集合S中。下面演示了用二進位制110110100表示集合{7,6,4,3,1}。
OK,有了這個思想,我們就可以把整數想象為二進位制的數,實際上,我們也知道,整數在機器裡面都是用0,1表示的,可以這麼說,0,1創造了計算機的整個世界。這就是為什麼判斷一個整數是不是奇數用if(n&1) n為奇數;(奇數用二進位制表示末尾一定是1)比用if(1 == n%1) n為奇數;快多了的原因。知道了表示,還要知道怎樣操作整數來表示集合,這點發明C語言的人早就為我們想到了。他們分別是&,|, ^.
好了,就看怎樣用程式碼實現吧:
#include<stdio.h>
void fullCombination(int n, int s) // 列印{1, 2, ..., n}的子集S
{
for(int i = 0; i < n; i++)
{
if(s&(1<<i))
printf("%d ", i+1); // 這裡利用了C語言“非0值都為真”的規定
}
printf("/n");
}
int main()
{
int n;
while(scanf("%d", &n) != EOF)
{
for(int i = 0; i < (1<<n); i++) // 列舉各子集所對應的編碼 0, 1, 2, ..., 2^n-1
fullCombination(n, i);
}
return 0;
}
/*
INPUT
3
OUTPUT
1
2
1 2
3
1 3
2 3
1 2 3
這段程式碼的效率肯定要比前面兩段程式碼快多了。不過不要得意太早,你輸入31試試?程式碼什麼也沒輸出。這是為什麼呢?1~30都能輸出他的所有子集,為什麼30以後的就不行了……仔細想想int是多少位你就明白了……所以還是應了那句話,出來混的,遲早是要還的,而前面兩段程式碼雖然效率低些,但只要記憶體足夠,原則上是能輸出1~UINT_MAX的子集。
我比較喜歡第三段程式碼。所以把第三段程式碼稍微修改一下就能完成老師的所提的問題了。修改後的程式碼如下:
#include<stdio.h>
int numOfOne(int n)//計算n轉換為二進位制後1的個數
{
int count = 0;
while(n)
{
if(n&1)
count++;
n>>=1;
}
return count;
}
void fullCombination(int n, int s, int k) // 列印{1, 2, ..., n}的子集S
{
int count=0;
for(int i = 0; i < n; i++)
{
if(s&(1<<i) && k==numOfOne(s))//s二進位制中1的個數決定了子集s中的元素的個數
{
printf("%d ", i+1); // 這裡利用了C語言“非0值都為真”的規定
count++;
}
}
if(k == count)
printf("/n");
}
int main()
{
int n, k;
while(scanf("%d %d", &n, &k) != EOF)
{
for(int i = 0; i < (1<<n); i++) // 列舉各子集所對應的編碼 0, 1, 2, ..., 2^n-1
fullCombination(n, i, k);
}
return 0;
}
/****************
4 2
1 2
1 3
2 3
1 4
2 4
3 4
5 3
1 2 3
1 2 4
1 3 4
2 3 4
1 2 5
1 3 5
2 3 5
1 4 5
2 4 5
3 4 5
***************/問題:(因為上面的子集生成的程式碼都不能解決如果輸入的數有相同的這一問題,顧有下面的這一題)
3、如果輸入n個數,求著n個數構成的所有子集,不允許輸出重複項。如
輸入
3
1 1 3
輸出
1
1 1
1 1 3
1 3
3
#include <stdio.h>
#define MAX_N 10
int rcl[MAX_N], num[MAX_N], used[MAX_N];
int m,n;
void unrepeat_combination(int index, int p)
{
int i;
for (i=0; i<index; i++)
{
printf("%d", rcl[i]);
if (i<index-1)
{
printf(" ");
}
else
printf("\n");
}
for (i=p; i<n; i++)
{
if (used[i]>0)
{
used[i]--;
rcl[index] = num[i];
unrepeat_combination(index+1, i);
used[i]++;
}
}
}
int read_data()
{
if (scanf("%d", &n)== EOF)
{
return 0;
}
int i, j, val;
m = 0;
for (i=0; i<n; i++)
{
scanf("%d", &val);
for (j=0; j<m; j++)
{
if (val == num[j])
{
used[j]++;
break;
}
}
if (j==m)
{
num[m] = val;
used[m] = 1;
m++;
}
}
return 1;
}
void main()
{
while(read_data())
{
unrepeat_combination(0, 0);
}
}
======================================================================================
總結:關於列舉排列與子集生成的大部分方法都整理出來了,借鑑了很多資料。希望能給自己梳理一下整個思路,能有所收穫!
另外:
1、輸入一個數組a[],裡面有n(1<=n<=1000)個數,給出陣列a[]所有數字的一個全排列,求他按照字典排序,這個全排列是所有排列中的第幾個。比如a[5] = {1, 1, 4, 5, 8};1 4 1 5 8是該全排列的第8個。
2、如果不曉得對全排列掌握得怎麼樣,請到POJ上提交你的程式碼,注意,請不要使用next_permutation();題目的連結為:
如果你能不使用next_permutation()把這5個題目AC,那麼,估計以後面試的時候全排列應該沒問題。等不用next_permutation()把那五個題目AC之後,再用next_permutation()爽一把吧。
3、同時考慮如何生成一個規定個數的子集,且子集裡的元素可以重複出現。
例如:
INPUT
6
1 2 4 6 7 9
OUTPUT
……
1 1 1 1 2 2
1 1 1 1 1 2
……
像是這種,輸入的資料沒有重複的,但是每個生成的小的排列內部,比如1 就可以重複使用多次,而且這個輸出序列元素個數是這輸入元素的個數決定的!
另外還有關於遞迴的過程梳理,一定要整理出一片部落格來!
