資料結構與演算法(c++)——跳躍表(skip list)
本文轉載自部落格:https://www.cnblogs.com/learnhow/p/6749648.html
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
今天要介紹一個這樣的資料結構:
- 單向連結
- 有序儲存
- 支援新增、刪除和檢索操作
- 連結串列的元素查詢接近線性時間
——跳躍表 Skip List
一、普通連結串列
對於普通連結來說,越靠前的節點檢索的時間花費越低,反之則越高。而且,即使我們引入複雜演算法,其檢索的時間花費依然為O(n)。為了解決長連結串列結構的檢索問題,一位名叫William Pugh的人於1990年提出了跳躍表結構。基本思想是——以空間換時間。
二、簡單跳躍表(Integer結構)
跳躍表的結構是多層的,通過從最高維度的表進行檢索再逐漸降低維度從而達到對任何元素的檢索接近線性時間的目的O(logn)。
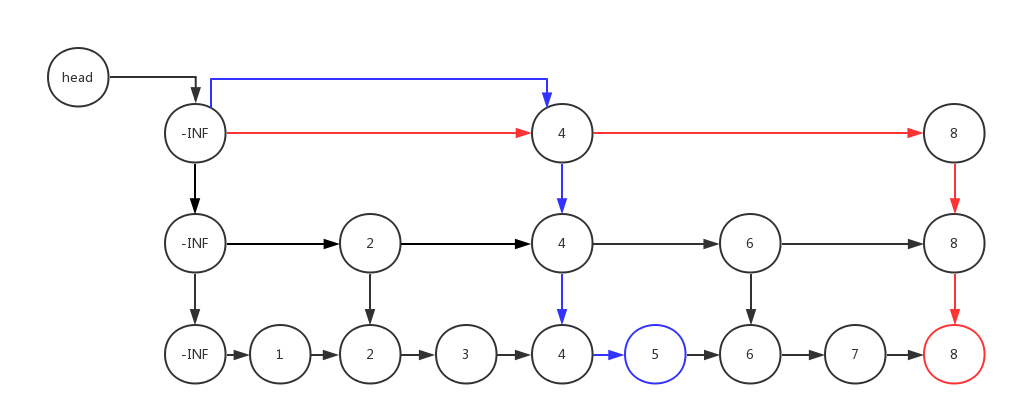
如圖:對節點8的檢索走紅色標記的路線,需要4步。對節點5的檢索走藍色路線,需要4步。由此可見,跳躍表本質上是一種網路佈局結構,通過增加檢索的維度(層數)來減少連結串列檢索中需要經過的節點數。理想跳躍表應該具備如下特點:包含有N個元素節點的跳躍表擁有log2N層,並且上層連結串列包含的節點數恰好等於下層連結串列節點數的1/2。但如此嚴苛的要求在演算法上過於複雜。因此通常的做法是:每次向跳躍表中增加一個節點就有50%的隨機概率向上層連結串列增加一個跳躍節點,並以此類推。
接下來,我們做如下規範說明:
- 跳躍表的層數,我們稱其維度。自頂向下,我們稱為降維,反之亦然。
- 表中,處於不同連結串列層的相同元素。我們稱為“同位素”。
- 最底層的連結串列,即包含了所有元素節點的連結串列是L1層,或稱基礎層。除此以外的所有連結串列層都稱為跳躍層。
以下是程式碼實現
#pragma once
#ifndef SKIPLIST_INT_H_
#define SKIPLIST_INT_H_
#include <cstdlib> /* srand, rand */
#include <ctime> /* time */
#include <climits> /* INT_MIN */
/* 簡單跳躍表,它允許簡單的插入和刪除元素,並提供O(logn)的查詢時間複雜度。 */
/*
SkipList_Int的性質
(1) 由很多層結構組成,level是通過一定的概率隨機產生的,基本是50%的產生機率。
(2) 每一層都是一個有序的連結串列,預設是升序,每一層的連結串列頭作為跳點。
(3) 最底層(Level 1)的連結串列包含所有元素。
(4) 如果一個元素出現在Level i 的連結串列中,則它在Level i 之下的連結串列也都會出現。
(5) 每個節點包含四個指標,但有可能為nullptr。
(6) 每一層連結串列橫向為單向連線,縱向為雙向連線。
*/
// Simple SkipList_Int 表頭始終是列表最小的節點
class SkipList_Int {
private:
/* 節點元素 */
struct node {
node(int val = INT_MIN) :value(val), up(nullptr), down(nullptr), left(nullptr), right(nullptr) {}
int value;
// 設定4個方向上的指標
struct node* up; // 上
struct node* down; // 下
struct node* left; // 左
struct node* right; // 右
};
private:
node* head; // 頭節點,查詢起始點
int lvl_num; // 當前連結串列層數
/* 隨機判斷 */
bool randomVal();
public:
SkipList_Int(): lvl_num(1) {
head = new node();
}
/* 插入新元素 */
void insert(int val);
/* 查詢元素 */
bool search(int val);
/* 刪除元素 */
void remove(int val);
};
#endif // !SKIPLIST_INT_H_我們需要實現插入、查詢和刪除三種操作。為了保證所有插入的元素均處於連結串列頭的右側。我們使用INT_MIN作為頭部節點。並且為了方便在不同維度的連結串列上轉移,連結串列頭節點包含up和down指標,普通整型節點之間的只存在down指標,水平方向上只存在right指標。
#include "SkipList_Int.h"
static unsigned int seed = NULL; // 隨機種子
bool SkipList_Int::randomVal() {
if (seed == NULL) {
seed = (unsigned)time(NULL);
}
::srand(seed);
int ret = ::rand() % 2;
seed = ::rand();
if (ret == 0) {
return true;
}
else {
return false;
}
}
void SkipList_Int::insert(int val) {
/* 首先查詢L1層 */
node* cursor = head;
node* new_node = nullptr;
while (cursor->down != nullptr) {
cursor = cursor->down;
}
node* cur_head = cursor; // 當前層連結串列頭
while (cursor->right != nullptr) {
if (val < cursor->right->value && new_node == nullptr) {
new_node = new node(val);
new_node->right = cursor->right;
cursor->right = new_node;
}
cursor = cursor->right; // 向右移動遊標
}
if (new_node == nullptr) {
new_node = new node(val);
cursor->right = new_node;
}
/* L1層插入完成 */
/* 上層操作 */
int cur_lvl = 1; // 當前所在層
while (randomVal()) {
cur_lvl++;
if (lvl_num < cur_lvl) { // 增加一層
lvl_num++;
node* new_head = new node();
new_head->down = head;
head->up = new_head;
head = new_head;
}
cur_head = cur_head->up; // 當前連結串列頭上移一層
cursor = cur_head; // 繼續獲取遊標
node* skip_node = nullptr; // 非L1層的節點
while (cursor->right != nullptr) {
if (val < cursor->right->value && skip_node == nullptr) {
skip_node = new node(val);
skip_node->right = cursor->right;
}
cursor = cursor->right;
}
if (skip_node == nullptr) {
skip_node = new node(val);
cursor->right = skip_node;
}
while (new_node->up != nullptr) {
new_node = new_node->up;
}
/* 連線上下兩個節點 */
skip_node->down = new_node;
new_node->up = skip_node;
}
}
bool SkipList_Int::search(int val) {
node* cursor = nullptr;
if (head == nullptr) {
return false;
}
/* 初始化遊標指標 */
cursor = head;
while (cursor->down != nullptr) { // 第一層循環遊標向下
while (cursor->right != nullptr) { // 第二層循環遊標向右
if (val <= cursor->right->value) { // 定位元素:於當前連結串列發現可定位座標則跳出迴圈...
break;
}
cursor = cursor->right;
}
cursor = cursor->down;
}
while (cursor->right != nullptr) { // L1層迴圈開始具體查詢
if (val > cursor->right->value) {
cursor = cursor->right; // 如果查詢的值大於右側值則遊標可以繼續向右
}
else if (val == cursor->right->value) { // 如果等於則表明已經找到節點
return true;
}
else if (val < cursor->right->value) { // 如果小於則表明不存在該節點
return false;
}
}
return false; // 完成遍歷返回false;
}
void SkipList_Int::remove(int val) {
node* cursor = head; // 獲得遊標
node* pre_head = nullptr; // 上一行的頭指標,刪除行時使用
while (true) {
node* cur_head = cursor; // 當前行頭指標
if (pre_head != nullptr) {
cur_head->up = nullptr;
pre_head->down = nullptr; // 解除上下級的指標
delete pre_head;
pre_head = nullptr; // 指標歸0
lvl_num--; // 層數-1
head = cur_head; // 重新指定起始指標
}
while (cursor != nullptr && cursor->right != nullptr) { // 在當前行中查詢val
if (val == cursor->right->value) {
node* delptr = cursor->right;
cursor->right = cursor->right->right;
delete delptr; // 析構找到的節點
}
cursor = cursor->right;
}
if (cur_head->right == nullptr) { // 判斷當前行是否還存在其它元素,如果不存在則刪除該行並將整個跳躍表降維
pre_head = cur_head;
}
if (cur_head->down == nullptr) {
break;
}
else {
cursor = cur_head->down;
}
}
}
以上程式碼演示的是簡單整型跳躍表的具體實現方法。它演示了一種最基本的跳躍,而它的問題也顯而易見。如果非整型物件,我們如何設計連結串列頭節點?普通物件如何實現排序?以及如何比較相等?為了解決這些問題,我們需要設計一種能夠支援各種型別物件的跳躍表。我們的思路是:
- 跳躍表應該支援泛型結構
- 排序規則由使用者來確定
- 連結串列頭節點必須是獨立的
三、泛型跳躍表
首先設計一個可直接比較的節點物件,過載運算子是一個不錯的選擇:
template<typename T>
class Entry {
private:
int key; // 排序值
T value; // 儲存物件
Entry* pNext;
Entry* pDown;
public:
// The Constructor
Entry(int k, T v) :value(v), key(k), pNext(nullptr), pDown(nullptr) {}
// The Copy-constructor
Entry(const Entry& e) :value(e.value), key(e.key), pNext(nullptr), pDown(nullptr) {}
public:
/* 過載運算子 */
bool operator<(const Entry& right) {
return key < right.key;
}
bool operator>(const Entry& right) {
return key > right.key;
}
bool operator<=(const Entry& right) {
return key <= right.key;
}
bool operator>=(const Entry& right) {
return key >= right.key;
}
bool operator==(const Entry& right) {
return key == right.key;
}
Entry*& next() {
return pNext;
}
Entry*& down() {
return pDown;
}
};
特別說明一下最後兩個方法的返回值是指標的引用,它可以直接作為左值。(Java程式設計師表示一臉懵逼)
然後,還需要設計一個獨立於檢索節點的連結串列頭物件:
struct Endpoint {
Endpoint* up;
Endpoint* down;
Entry<T>* right;
};
隨機判斷函式沒有太大變化,只是將種子seed的儲存位置從函式外放到了物件中。以下是完整程式碼:
#pragma once
#ifndef SKIPLIST_ENTRY_H_
#define SKIPLIST_ENTRY_H_
/* 一個更具備代表性的泛型版本 */
#include <ctime>
#include <cstdlib>
template<typename T>
class Entry {
private:
int key; // 排序值
T value; // 儲存物件
Entry* pNext;
Entry* pDown;
public:
// The Constructor
Entry(int k, T v) :value(v), key(k), pNext(nullptr), pDown(nullptr) {}
// The Copy-constructor
Entry(const Entry& e) :value(e.value), key(e.key), pNext(nullptr), pDown(nullptr) {}
public:
/* 過載運算子 */
bool operator<(const Entry& right) {
return key < right.key;
}
bool operator>(const Entry& right) {
return key > right.key;
}
bool operator<=(const Entry& right) {
return key <= right.key;
}
bool operator>=(const Entry& right) {
return key >= right.key;
}
bool operator==(const Entry& right) {
return key == right.key;
}
Entry*& next() {
return pNext;
}
Entry*& down() {
return pDown;
}
};
template<typename T>
class SkipList_Entry {
private:
struct Endpoint {
Endpoint* up;
Endpoint* down;
Entry<T>* right;
};
struct Endpoint* header;
int lvl_num; // level_number 已存在的層數
unsigned int seed;
bool random() {
srand(seed);
int ret = rand() % 2;
seed = rand();
return ret == 0;
}
public:
SkipList_Entry() :lvl_num(1), seed(time(0)) {
header = new Endpoint();
}
/* 插入新元素 */
void insert(Entry<T>* entry) { // 插入是一系列自底向上的操作
struct Endpoint* cur_header = header;
// 首先使用連結串列header到達L1
while (cur_header->down != nullptr) {
cur_header = cur_header->down;
}
/* 這裡的一個簡單想法是L1必定需要插入元素,而在上面的各跳躍層是否插入則根據random確定
因此這是一個典型的do-while迴圈模式 */
int cur_lvl = 0; // current_level 當前層數
Entry<T>* temp_entry = nullptr; // 用來臨時儲存一個已經完成插入的節點指標
do {
Entry<T>* cur_cp_entry = new Entry<T>(*entry); // 拷貝新物件
// 首先需要判斷當前層是否已經存在,如果不存在增新增
cur_lvl++;
if (lvl_num < cur_lvl) {
lvl_num++;
Endpoint *new_header = new Endpoint();
new_header->down = header;
header->up = new_header;
header = new_header;
}
// 使用cur_lvl作為判斷標準,!=1表示cur_header需要上移並連線“同位素”指標
if (cur_lvl != 1) {
cur_header = cur_header->up;
cur_cp_entry->down() = temp_entry;
}
temp_entry = cur_cp_entry;
// 再需要判斷的情況是當前所在連結串列是否已經有元素節點存在,如果是空連結串列則直接對右側指標賦值並跳出迴圈
if (cur_header->right == nullptr) {
cur_header->right = cur_cp_entry;
break;
}
else {
Entry<T>* cursor = cur_header->right; // 建立一個遊標指標
while (true) { // 於當前連結串列迴圈向右尋找可插入點,並在找到後跳出當前迴圈
if (*cur_cp_entry < *cursor) { // 元素小於當前連結串列所有元素,插入連結串列頭
cur_header->right = cur_cp_entry;
cur_cp_entry->next() = cursor;
break;
}
else if (cursor->next() == nullptr) { // 元素大於當前連結串列所有元素,插入連結串列尾
cursor->next() = cur_cp_entry;
break;
}
else if (*cur_cp_entry < *cursor->next()) { // 插入連結串列中間
cur_cp_entry->next() = cursor->next();
cursor->next() = cur_cp_entry;
break;
}
cursor = cursor->next(); // 右移動遊標
}
}
} while(random());
}
/* 查詢元素 */
bool search(Entry<T>* entry) const {
if (header->right == nullptr) { // 判斷連結串列頭右側空指標
return false;
}
Endpoint* cur_header = header;
// 在lvl_num層中首先找到可以接入的點
for (int i = 0; i < lvl_num; i++) {
if (*entry < *cur_header->right) {
cur_header = cur_header->down;
}
else {
Entry<T>* cursor = cur_header->right;
while (cursor->down() != nullptr) {
while (cursor->next() != nullptr) {
if (*entry <= *cursor->next()) {
break;
}
cursor = cursor->next();
}
cursor = cursor->down();
}
while (cursor->next() != nullptr) {
if (*entry > *cursor->next()) {
cursor = cursor->next();
}
else if (*entry == *cursor->next()) {
return true;
}
else {
return false;
}
}
return false; // 節點大於L1最後一個元素節點,返回false
}
}
return false; // 找不到接入點,則直接返回false;
}
/* 刪除元素 */
void remove(Entry<T>* entry) {
if (header->right == nullptr) {
return;
}
Endpoint* cur_header = header;
Entry<T>* cursor = cur_header->right;
int lvl_counter = lvl_num; // 因為在刪除的過程中,跳躍表的層數會中途發生變化,因此應該在進入迴圈之前要獲取它的值。
for (int i = 0; i < lvl_num; i++) {
if (*entry == *cur_header->right) {
Entry<T>* delptr = cur_header->right;
cur_header->right = cur_header->right->next();
delete delptr;
}
else {
Entry<T> *cursor = cur_header->right;
while (cursor->next() != nullptr) {
if (*entry == *cursor->next()) { // 找到節點->刪除->跳出迴圈
Entry<T>* delptr = cursor->next();
cursor->next() = cursor->next()->next();
delete delptr;
break;
}
cursor = cursor->next();
}
}
// 向下移動連結串列頭指標的時候需要先判斷當前連結串列中是否還存在Entry節點
if (cur_header->right == nullptr) {
Endpoint* delheader = cur_header;
cur_header = cur_header->down;
header = cur_header;
delete delheader;
lvl_num--;
}
else {
cur_header = cur_header->down;
}
}
}
};
#endif // !SKIPLIST_ENTRY_H_
後記:網上有不少別人提供的具體實現。不過感覺相互複製的居多。學習沒有近路可言,抄小路取得的“成功”並不完全屬於自己。作為一個或許入行有些晚的程式設計師,我時刻驚醒自己要想在這條路上走的更遠更穩,必須依靠紮實的基本功。什麼是基本功?無非“語言”,“資料結構與演算法”,“設計模式”。但是這些東西往往對於企業或專案而言並不被看重。理由很簡單,他們只關心你能否完成工作以及足夠快速——程式碼質量或個人成長於客戶於僱主皆為浮雲。
但對於自己來說,試著接觸那些“本源”性的知識是對未來的投資。如果你和我一樣希望5年後的自己能夠更加自由的生活。就請暫時忽略專案經理的催促和無理客戶的抱怨,也請放下在領導面前所做出的表面文章。靜下來,對於大家都好。

