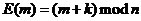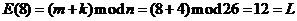古典密碼演算法曾被廣泛應用，大都比較簡單，使用手工和機械操作來實現加密和解密。它的主要應用物件是文字資訊，利用密碼演算法實現文字資訊的加密和解密。下面介紹兩種常見的具有代表性的古典密碼演算法，以幫助讀者對密碼演算法建立一個初步的印象。

1. 替代密碼

替代密碼的原理是使用替代法進行加密，就是將明文由其它的字母、數字或符合所代替後形成密文。這裡每個明文字母對應的密文字母可能是一個，也可能是多個。接收者對密文進行逆向替換即可得到明文。替代密碼有五種表現形式：

1單表代替

即簡單替代密碼或者稱為單字母代替，明文字母表中的一個字元對應密文字母表中的一個字元。這是所有加密中最簡單的方法。 

2多名碼代替

就是將明文字母表中的字元對映為密文字母表中的多個字元。多名碼簡單代替早在1401年就由DuchyMantua公司使用。在英文中，母音字母出現頻率最高，降低對應密文字母出現頻率的一種方法就是使用多名碼，如e可能被密文5、13或25替代。 

3多音碼代替

就是將多個明文字元代替為一個密文字元。比如將字母“i” 和“j”對應為“K”，“v”和“w”代替為“L”最古老的這種多字母加密始見於1563年由波他的《密寫評價》（De furtiois literarum notis）一書。 

4多表代替

即由多個簡單代替組成，也就是使用了兩個或兩個以上的代替表。比如使用有5個簡單代替表的代替密碼，明文的第一個字母用第一個代替表，第二個字母用第二個表，第三個字母用第三個表，以此類推，迴圈使用這五張代替表。多表代替密碼由萊昂

下面我們介紹一種典型的單表替代密碼——凱撒(Caesar)密碼，又叫迴圈移位密碼。它的加密方法就是將明文中的每個字母用字母表中該字母后的第R個字母來替換，達到加密的目的。它的加密過程可以表示為下面的函式：

其中，ｍ為明文字母在字母表中的位置數；ｎ為字母表中的字母個數；ｋ為金鑰； 為密文字母在字母表中對應的位置數。

    例如：對於明文字母H，其在字母表中的位置數為8，設，則按照上式計算出來的密文為L，計算過程如下：

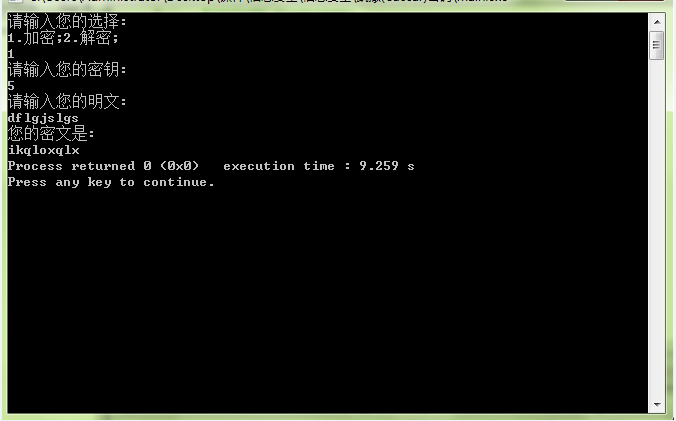
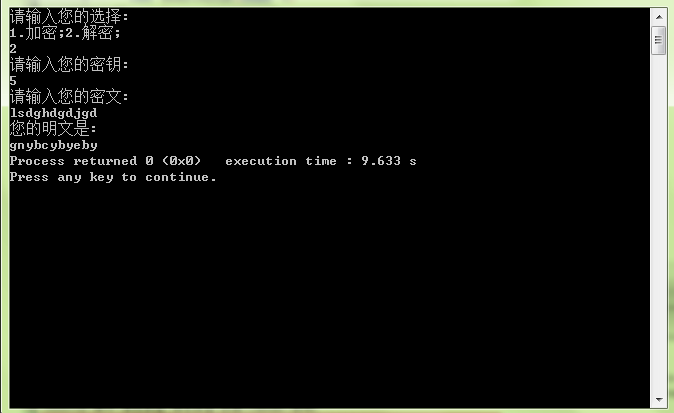
程式碼為：

#include <iostream>
using namespace std;
# define N 26
int searchnum(char t)
    {
        char r;
        char str[26];
        for(int i=1,r='A';i<=N;i++,r++)
        {
            str[i]=r;
        }
        for(int i=1;i<=N;i++)
        {
            if(t==str[i])
            return i;
        }
    }
char searchchar(int t)
{
        char r;
        char str[26];
        for(int i=1,r='A';i<=N;i++,r++)
        {
            str[i]=r;
        }
        for(int i=1;i<=N;i++)
        {
            if(t==i)
            return str[i];
        }
}
void jiami()
{
    char str[50];
    int k;
    cout<<"請輸入您的金鑰:"<<endl;
    //int m;
    //char s;
    cin>>k;
    cout<<"請輸入您的明文:"<<endl;
    cin>>str;
    for(int i=0;str[i]!='\0';i++)
    {
        int a,b;
        char ch=str[i];
        int m=searchnum(ch);
        a=m+k;
        b=a%26;
        char c=searchchar(b);
        str[i]=c;
    }
    cout<<"您的密文是:"<<endl;
    for(int i=0;str[i]!='\0';i++)
    {
        cout<<str[i];
    }
}
void jiemi()
{
    char str[50];
    int k;
    cout<<"請輸入您的金鑰:"<<endl;
    //int m;
    //char s;
    cin>>k;
    cout<<"請輸入您的密文:"<<endl;
    cin>>str;
    for(int i=0;str[i]!='\0';i++)
    {
        int a,b;
        char ch=str[i];
        int m=searchnum(ch);
        if(m<k)
        {
            a=m+N-k;
            b=a%N;
        }
        else if(m>k)
        {
            a=m-k;
            b=a%N;
        }
        else
        {
            b=N;
        }
        char c=searchchar(b);
        str[i]=c;
    }
    cout<<"您的明文是:"<<endl;
    for(int i=0;str[i]!='\0';i++)
    {
        cout<<str[i];
    }
}
int main()
{
    int choice;
    cout<<"請輸入您的選擇:"<<endl;
    cout<<"1.加密;2.解密;"<<endl;
    cin>>choice;
    switch (choice)
    {
        case 1:
            jiami();
            break;
        case 2:
            jiemi();
            break;
        default:
            break;
    }
       // cout << searchnum(s)<< endl;
    return 0;
}
 

實現加密與解密