深入淺出解釋FFT(七)——fft求頻譜圖和功率譜密度圖
頻譜圖:
聲音訊率與能量的關係用頻譜表示。在實際使用中,頻譜圖有三種,即線性振幅譜、對數振幅譜、自功率譜。線性振幅譜的縱座標有明確的物理量綱,是最常用的。對數振幅譜中各譜線的振幅都作了對數計算,所以其縱座標的單位是dB(分貝)。這個變換的目的是使那些振幅較低的成分相對高振幅成分得以拉高,以便觀察掩蓋在低幅噪聲中的週期訊號。自功率譜是先對測量訊號作自相關卷積,目的是去掉隨機干擾噪聲,保留並突出週期性訊號,損失了相位特徵,然後再作傅立葉變換。自功率譜圖使得週期性訊號更加突出。
功率譜圖:又叫功率譜密度圖
功率譜是功率譜密度函式的簡稱,它定義為單位頻帶內的訊號功率。它表示了訊號功率隨著頻率的變化情況,即訊號功率在頻域的分佈狀況。
時域和頻域能量相等。
Parseval 定理
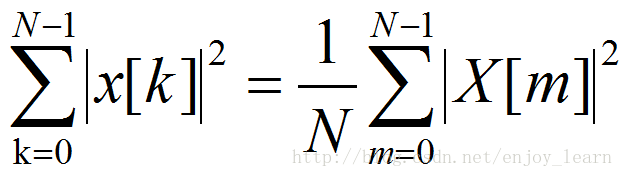
有限上序列x{k}的離散fourier變換是正交變換,滿足Parseval能量守恆定理,反映了序列在時域的能量等於其變換域的能量。
關於能量定義:訊號幅度平方的積分,如果是數字訊號,能量就是各點訊號幅度值平方後的求和。
論壇帖子中關於等式關係給出的結論是:
求和 (x(tn)^2)T=RMS^2*Ttotal=求和(P(fn))
△f*Ttotal
其中,x(tn)是n個x(t)時域取樣資料,T是時間間隔,Ttotal是時間總長,
P(fn)是第n個功率譜密度值,△f是FFT頻率間隔
最後的結論是相等的,但是訊號的能量到底是sum(x.^2),還是sum(x.^2)*T?按照定義來說是前者沒錯。但是絕對的能量計算若不跟取樣頻率(取樣間隔)結合起來,又有什麼對比作用?
同樣1000個點幅值為1,一組波形是1秒內採到的,另一組波形是10秒內採到的,按公式算,訊號的能量相等,按sum(x.^2)*T計算,10秒採集到的波形的能量更大。
現實情況中,比較兩個波形的能量或有效值,都是取樣率相同,取樣時間相同,所有不會遇到如此糾結的問題。
生成一組訊號:
fs=1000;
>> N=1000;
>> n=0:N-1;
>> t=n/fs;
>> x=sin(2*pi*100*t);
>> nfft=1024;
>> deltF=fs/nfft;
>> window=hanning(N);
>> %直接法,periodogram函式得到的功率譜密度
>>[Pxx_period,f_period]=periodogram(x,window,nfft,fs);
> noverlap=50;
>>[Pxx_welch,f_welch]=pwelch(x,window,noverlap,nfft,fs);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
計算原始訊號的有效值為: 0.0224
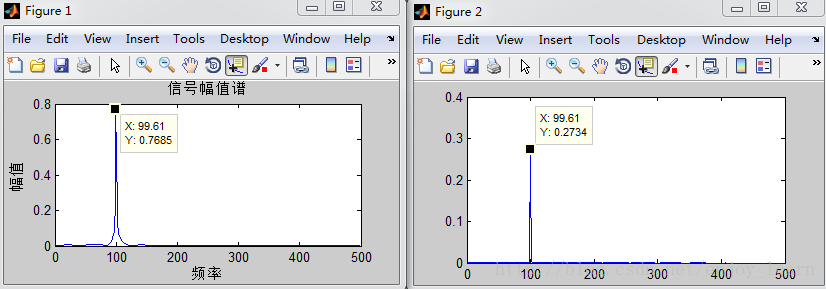
畫出頻譜與功率譜密度為:
幅值譜的幅值理論上應為1,不到1的原因是fft變換的點數與取樣點數不同所致。
利用FFT幅值譜的平方/N ,畫功率譜密度結果跟上右圖差不多。
xw=1.633*x.*window'; % 加漢寧窗(恢復係數為1.633),能量修正係數使加窗後能量保證不變
mag=abs(fft(xw,nfft));
Pxx_1=mag.^2/N/fs;
f=(0:nfft/2-1)/nfft*fs;
plot(f,Pxx_11(1:512)*2),title('Pxx_11')- 1
- 2
- 3
- 4
- 5
- 1
- 2
- 3
- 4
- 5
關於功率譜密度計算,先做自相關計算,再做FFT也能得到功率譜密度。
最後結果為:
summary:
當取樣點數=nfft時,deltF*N/fs=1;
功率譜密度直接求和即是頻域能量。
用幅值譜的平方估計頻域能量時,除完點數,還要除以取樣頻率。
時域能量要*取樣間隔(1/fs)
有效值的平方*取樣時間=時域能量;