圖的基本演算法(BFS和DFS)
圖是一種靈活的資料結構,一般作為一種模型用來定義物件之間的關係或聯絡。物件由頂點(V)表示,而物件之間的關係或者關聯則通過圖的邊(E)來表示。
圖可以分為有向圖和無向圖,一般用G=(V,E)來表示圖。經常用鄰接矩陣或者鄰接表來描述一副圖。
在圖的基本演算法中,最初需要接觸的就是圖的遍歷演算法,根據訪問節點的順序,可分為廣度優先搜尋(BFS)和深度優先搜尋(DFS)。
廣度優先搜尋(BFS)
廣度優先搜尋在進一步遍歷圖中頂點之前,先訪問當前頂點的所有鄰接結點。
a .首先選擇一個頂點作為起始結點,並將其染成灰色,其餘結點為白色。
b. 將起始結點放入佇列中。
c. 從佇列首部選出一個頂點,並找出所有與之鄰接的結點,將找到的鄰接結點放入佇列尾部,將已訪問過結點塗成黑色,沒訪問過的結點是白色。如果頂點的顏色是灰色,表示已經發現並且放入了佇列,如果頂點的顏色是白色,表示還沒有發現
d. 按照同樣的方法處理佇列中的下一個結點。
基本就是出隊的頂點變成黑色,在佇列裡的是灰色,還沒入隊的是白色。
用一副圖來表達這個流程如下:
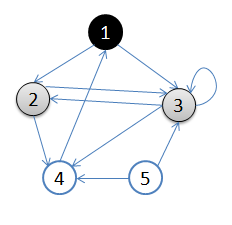
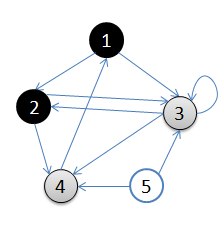
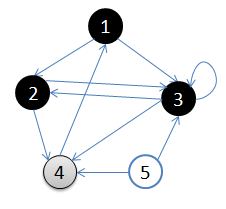

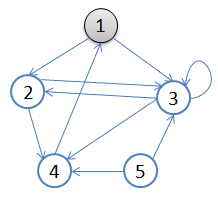
從頂點1開始進行廣度優先搜尋:
1. 初始狀態,從頂點1開始,佇列={1}
2. 訪問1的鄰接頂點,1出隊變黑,2,3入隊,佇列={2,3,}
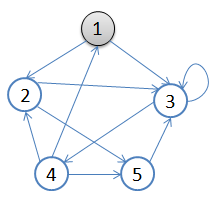
3. 訪問2的鄰接結點,2出隊,4入隊,佇列={3,4}
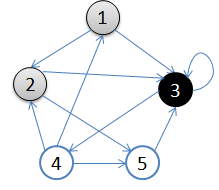
4. 訪問3的鄰接結點,3出隊,佇列={4}
5. 訪問4的鄰接結點,4出隊,佇列={ 空}
結點5對於1來說不可達。
上面的圖可以通過如下鄰接矩陣表示:
int maze[5][5] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 1, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0 } BFS核心程式碼如下:
#include <iostream>
#include <queue>
#define N 5
using namespace std;
int maze[N][N] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 1, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0 }
};
int visited[N + 1] = { 0, };
void BFS(int start)
{
queue<int> Q;
Q.push(start);
visited[start] = 1 深度優先搜尋(DFS)
深度優先搜尋在搜尋過程中訪問某個頂點後,需要遞迴地訪問此頂點的所有未訪問過的相鄰頂點。
初始條件下所有節點為白色,選擇一個作為起始頂點,按照如下步驟遍歷:
a. 選擇起始頂點塗成灰色,表示還未訪問
b. 從該頂點的鄰接頂點中選擇一個,繼續這個過程(即再尋找鄰接結點的鄰接結點),一直深入下去,直到一個頂點沒有鄰接結點了,塗黑它,表示訪問過了
c. 回溯到這個塗黑頂點的上一層頂點,再找這個上一層頂點的其餘鄰接結點,繼續如上操作,如果所有鄰接結點往下都訪問過了,就把自己塗黑,再回溯到更上一層。
d. 上一層繼續做如上操作,知道所有頂點都訪問過。
用圖可以更清楚的表達這個過程:
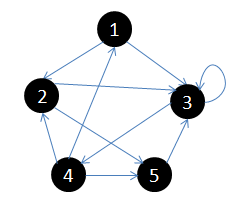
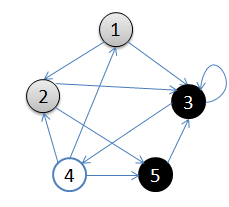
從頂點1開始做深度搜索:
1. 初始狀態,從頂點1開始
2. 依次訪問過頂點1,2,3後,終止於頂點3
3. 從頂點3回溯到頂點2,繼續訪問頂點5,並且終止於頂點5
4. 從頂點5回溯到頂點2,並且終止於頂點2
5. 從頂點2回溯到頂點1,並終止於頂點1
6. 從頂點4開始訪問,並終止於頂點4
上面的圖可以通過如下鄰接矩陣表示:
int maze[5][5] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};DFS核心程式碼如下(遞迴實現):
#include <iostream>
#define N 5
using namespace std;
int maze[N][N] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
int visited[N + 1] = { 0, };
void DFS(int start)
{
visited[start] = 1;
for (int i = 1; i <= N; i++)
{
if (!visited[i] && maze[start - 1][i - 1] == 1)
DFS(i);
}
cout << start << " ";
}
int main()
{
for (int i = 1; i <= N; i++)
{
if (visited[i] == 1)
continue;
DFS(i);
}
return 0;
}非遞迴實現如下,藉助一個棧:
#include <iostream>
#include <stack>
#define N 5
using namespace std;
int maze[N][N] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
int visited[N + 1] = { 0, };
void DFS(int start)
{
stack<int> s;
s.push(start);
visited[start] = 1;
bool is_push = false;
while (!s.empty())
{
is_push = false;
int v = s.top();
for (int i = 1; i <= N; i++)
{
if (maze[v - 1][i - 1] == 1 && !visited[i])
{
visited[i] = 1;
s.push(i);
is_push = true;
break;
}
}
if (!is_push)
{
cout << v << " ";
s.pop();
}
}
}
int main()
{
for (int i = 1; i <= N; i++)
{
if (visited[i] == 1)
continue;
DFS(i);
}
return 0;
}有的DFS是先訪問讀取到的結點,等回溯時就不再輸出該結點,也是可以的。演算法和我上面的區別就是輸出點的時機不同,思想還是一樣的。DFS在環監測和拓撲排序中都有不錯的應用。
PS: 圖文均為本人原創,畫了好幾個小時,轉載註明出處,尊重知識勞動,謝謝~