#資料說明

LFW全稱為Labeled Faces in the Wild, 是一個應用於人臉識別問題的資料庫，更多內容檢視官方網站：http://vis-www.cs.umass.edu/lfw

LFW語料圖片，每張圖片都有人名Label標記。每個人可能有多張不同情況下情景下的圖片。如George W Bush 有530張圖片，而有一些人名對應的圖片可能只有一張或者幾張。我們將選取出現最多的人名作為人臉識別的類別，如本實驗中選取出現頻數超過70的人名為類別， 那麼共計1288張圖片。其中包括Ariel Sharon, Colin Powell, Donald Rumsfeld, George W Bush, Gerhard Schroeder, Hugo Chavez , Tony Blair等7個人名。

#問題描述

通過對7個人名的提取特徵和標記，進行新輸入的照片進行標記人名。這是一個多分類的問題，在本資料集合中類別數目為7. 這個問題的解決，不僅可以應用於像公司考勤一樣少量人員的識別，也可以應用到新資料的標註中。語料庫進一步標註，將進一步擴大訓練資料集合資料量，從而進一步提高人臉識別的精確度。因此，對於圖片的人名正確標註問題，或者這個多分類問題的研究和使用是有應用價值的。

#資料處理

訓練與測試資料中樣本數量為1288，對樣本圖片進行下采樣後特徵數為1850，所有人臉的Label數目為7。
首先將資料集劃分為訓練集合和測試集合，測試集合佔25%(一般應該10%或者20%)，訓練資料進行訓練過程中，將分為訓練集合和驗證集合。通過驗證集合選擇最優模型，使用測試結合測試模型效能。
其次，通過對訓練集合PCA分解，提取特徵臉，提高訓練速度，防止過度擬合。圖片 1是關於不同的特徵所佔的總方差的比率關係，從中可以看出，關鍵特徵主要集中在前50個。圖片 2 是關於圖片 1的累計分佈圖。從曲線中可以看出，當特徵臉數目為50時，約佔85%的資料資訊，特徵臉資料為100時，約佔總資訊量的90%左右。經過測試，最佳分類結果時，特徵臉數目為80 .此時約佔88%的總體方差。

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt

from sklearn import linear_model, decomposition, datasets
from sklearn.pipeline import Pipeline
from sklearn.grid_search import GridSearchCV

logistic = linear_model.LogisticRegression()

pca = decomposition.PCA()
pipe = Pipeline(steps=[('pca'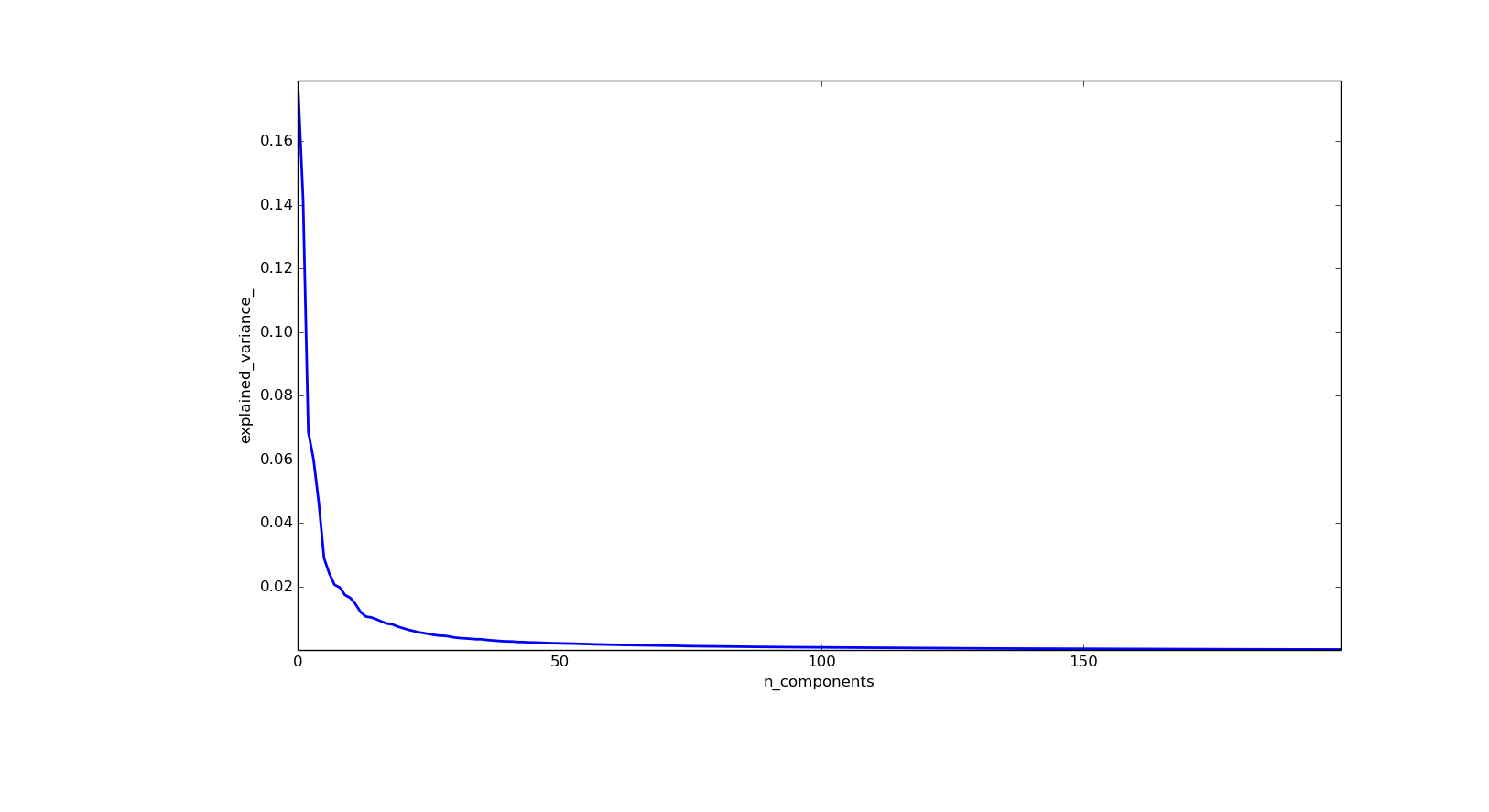
 
, pca), ('logistic', logistic)])

digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target

###############################################################################
# Plot the PCA spectrum
pca.fit(X_digits)

plt.figure(1, figsize=(4, 3))
plt.clf()
plt.axes([.2, .2, .7, .7])
plt.plot(pca.explained_variance_, linewidth=2)
plt.axis('tight')
plt.xlabel('n_components')
plt.ylabel('explained_variance_')

###############################################################################
# Prediction

n_components = [10, 20, 25, 30, 35, 40, 50, 64]#[i for i in range(1,65)]#
Cs = np.logspace(-4, 4, 3)

estimator = GridSearchCV(pipe,
                         dict(pca__n_components=n_components,
                              logistic__C=Cs))
estimator.fit(X_digits, y_digits)

plt.axvline(estimator.best_estimator_.named_steps['pca'].n_components,
            linestyle=':', label='n_components chosen')
plt.legend(prop=dict(size=12))
plt.show()

圖片1: 不同特徵選取數目的方差比率大小， 比率大小是按照從大到小的順序排列的，從曲線中可以看出，最大的一維約佔總體方差的18%

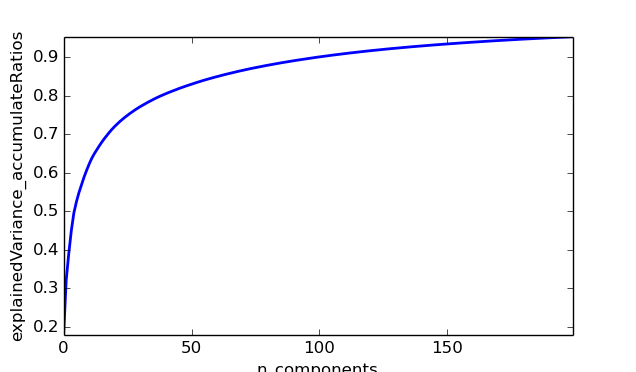
圖片 2： 不同特徵選取數目的方差累計比率曲線，從曲線中可以看出，當特徵臉數目為50時，約佔85%的資料資訊，特徵臉資料為100時，約佔總資訊量的90%左右經過測試，最佳分類結果時，特徵臉數目為80.此時約佔88%的總體方差。
因為不同的人有多個不同角度的照片，如果提取特徵臉過多，會導致過度擬合，從而測試結果不理想，如果使用特徵臉過少，則會導致人臉多類過程區分度不高而使得部分結果分類錯誤。而在LFW資料集合中，使用特徵臉數目為80時效果最佳是可以理解的。圖片 3 顯示了前16個特徵臉。

圖片 3：對PCA降維度結果中16個特徵臉先行呈現效果圖
當然，數字影象處理常用的特徵降維中NMF分解前幾年取得了很多成果，有機會可以使用NMF分級進行特徵提取和降維。

#模型訓練與結果

訓練程式碼

from __future__ import print_function

from time import time
import logging
import matplotlib.pyplot as plt

from sklearn.cross_validation import train_test_split
from sklearn.datasets import fetch_lfw_people
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import RandomizedPCA
from sklearn.svm import SVC


print(__doc__)

# Display progress logs on stdout
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')


###############################################################################
# Download the data, if not already on disk and load it as numpy arrays

lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)

# introspect the images arrays to find the shapes (for plotting)
n_samples, h, w = lfw_people.images.shape

# for machine learning we use the 2 data directly (as relative pixel
# positions info is ignored by this model)
X = lfw_people.data
n_features = X.shape[1]

# the label to predict is the id of the person
y = lfw_people.target
target_names = lfw_people.target_names
n_classes = target_names.shape[0]

print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)


###############################################################################
# Split into a training set and a test set using a stratified k fold

# split into a training and testing set
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=42)


###############################################################################
# Compute a PCA (eigenfaces) on the face dataset (treated as unlabeled
# dataset): unsupervised feature extraction / dimensionality reduction
n_components = 80

print("Extracting the top %d eigenfaces from %d faces"
      % (n_components, X_train.shape[0]))
t0 = time()
pca = RandomizedPCA(n_components=n_components, whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))

eigenfaces = pca.components_.reshape((n_components, h, w))

print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))


###############################################################################
# Train a SVM classification model

print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C': [1,10, 100, 500, 1e3, 5e3, 1e4, 5e4, 1e5],
              'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid)
clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)

print(clf.best_estimator_.n_support_)
###############################################################################
# Quantitative evaluation of the model quality on the test set

print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca)
print("done in %0.3fs" % (time() - t0))

print(classification_report(y_test, y_pred, target_names=target_names))
print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))


###############################################################################
# Qualitative evaluation of the predictions using matplotlib

def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
    """Helper function to plot a gallery of portraits"""
    plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
    plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
    for i in range(n_row * n_col):
        plt.subplot(n_row, n_col, i + 1)
        # Show the feature face
        plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
        plt.title(titles[i], size=12)
        plt.xticks(())
        plt.yticks(())


# plot the result of the prediction on a portion of the test set

def title(y_pred, y_test, target_names, i):
    pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
    true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
    return 'predicted: %s\ntrue:      %s' % (pred_name, true_name)

prediction_titles = [title(y_pred, y_test, target_names, i)
                     for i in range(y_pred.shape[0])]

plot_gallery(X_test, prediction_titles, h, w)

# plot the gallery of the most significative eigenfaces

eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)

plt.show()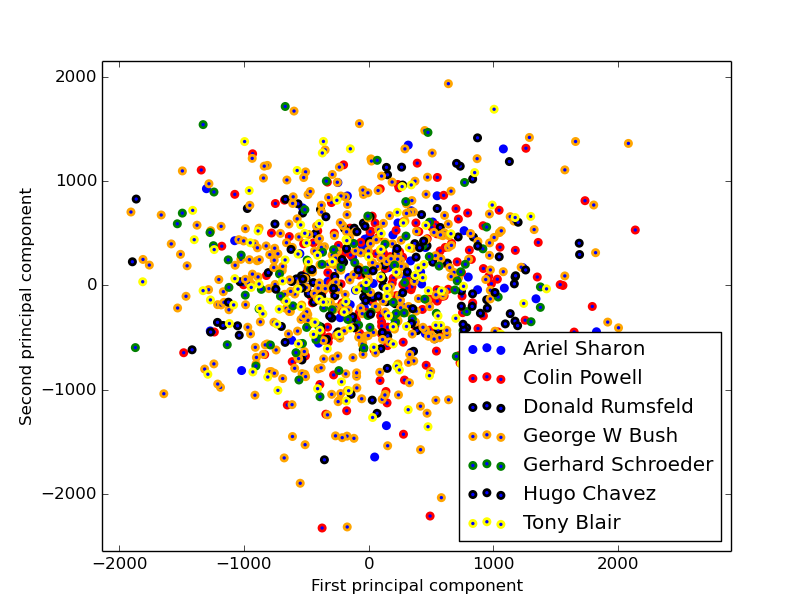

圖片 4 實驗資料在二維空間中分佈情況，可以看出該資料集如果使用線性模型進行分類，效果將很差；我們將從非線性模型帶核的SVM入手，解決該分類問題
分類模型將採用SVM分類器進行分類，其中核函式：
f=exp(−γ||x−x′||2)
我們將對核函式中的 γ 進行引數評估優化，此外對不同特徵的權重進行優化，通過交叉驗證和網格搜尋方式，查詢到最佳模型為γ=0.01， C = 10時，平均正確率達到90%，如表格 1所示。
表格 1: 關於測試集合人名標記結果的正確率，召回率和F1

這麼高的準確率，是由於我們僅僅選取了每個標識人名數目> 70的人名，但是大量的僅僅出現1次的人名存在。如果考慮這種資料稀疏性，將大大降低結果的準確率。但是，真實應用中，資料稀疏性問題是不得不考慮的問題。

圖片 5： 預測人名正確結果展示

#未來工作

本文中使用PCA實現特徵臉提取，也可以使用其他特徵提取方式進行降維。比如NMF實現矩陣分解在數字影象處理中的應用，實現NMF在人臉識別中的特徵分解。當前使用的訓練資料集使用的最小標記資料為70，當標記訓練資料比較稀疏的時候，能否利用未標記資料提供正確率。後面的研究中將注意這兩個方面的問題。

#參考文章