機器學習(五)降維技術---主成分分析、因子分析
機器學習(五)降維技術---主成分分析、因子分析
降維(處理線性問題為主)
一提到降維這個詞,大家可能就會覺得非常高大上,到底是什麼東西呢?降維通俗來講就是把原先多個指標的計算降維為少量幾個經過優化指標的計算,可能大家還是不理解,舉個例子就是本來拿來參加建模的特徵有100個,但是太多了,經過一些特徵的一些組合變換衍生出一些新的特徵變數,取對結果影響比較大的一些新的特徵變數,現在問題就可以從一開始100個特徵變為現在的3到5個特徵。需要注意的是新衍生的特徵變數一般是100個原始特徵向量的線性組合。一般做了降維技術自然地多重共線性也就消除了,不需要額外做多重共線性內容
降維一般對於迴歸、分類、聚類都適用,那一般降維都有什麼方法呢?
- 主成分分析
- 因子分析
降維技術和之前的Lasso和嶺迴歸有什麼區別呢?
Lasso和嶺迴歸:沒有對變數進行線性組合出新變數,直接捨棄一些原始變數建模
降維技術:不捨棄原始變數,直接對原始特徵線性組合出新特徵變數
主成分分析
下面我們下先來學習一下主成分分析,簡單來說就是n個特徵向量空間裡面找一些方向,使得這些方向上資料的方差最大
簡單來說就是先求方差矩陣之後轉換為相關係數矩陣,再求特徵值、特徵向量、看累計貢獻率選出3-5個維度、檢視這些維度的載荷(由原始特徵如何線性組成)、用這些新的維度去建模,假如模型擬合很好,用業務解釋這幾個維度(主成分分析是從數學角度去解決問題,業務解釋性不強)
這些方向就是新的特徵向量(也就是新的維度),之後用n個特徵向量空間解釋,轉化為n個特徵的線性組合
為什麼這樣考慮呢?
假如某一個特徵全是0,另一個特徵取值多種多樣,顯然特徵全是0的對我們模型意義不大,其資料差異小,如何衡量資料差異呢?用方差。


主成分分析的幾何圖,如圖F1的方差(截距明顯比F2長)比F2的大,所以F2可以考慮捨棄,其中F1和F2是新衍生出的維度

主成分分析的數學模型(理論性強,可以不瞭解)


我們先來了解一些名詞
(累計貢獻率,應為之前我們不是說![]() ,這裡的解釋變異就是指主成分的累計貢獻率)
,這裡的解釋變異就是指主成分的累計貢獻率)
(載荷也要了解一下,就是新的維度由原始維度如何線性組合而成,係數的確定)


注意
主成分方向對資料值的範圍高度敏感,如果特徵值不同維度應該先對特徵標準化處理,讓各特徵具有相同的重要性。



可能說了這麼久,大家還是雲裡霧裡的,我們就舉一個分類小例子吧(還可以去應用迴歸、聚類問題)


通過R語言主成分分析,畫框框那裡表示累計貢獻率,衍生出4個維度,發現兩個維度已經可以了

看一下這些衍生變數的載荷(看下面Z1和這張圖結合看就懂了)
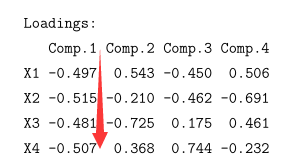

之後從業務上解釋這些新的變數

因子分析
簡單來說就是樣本求出協方差矩陣,之後求出因子,作因子旋轉,業務解釋



咋一眼看好像和主成分分析沒什麼區別,但是還是有區別的(所以一般因子分析優於主成分分析,結合業務來的)

數學模型


性質(畫框框那個乘以正交矩陣,後面因子旋轉主要是用了這條性質)



紅色箭頭指的意思是
![]()
解決模型方法有
- 主成分法


- 主因子法

- 極大似然法

方差最大的正交旋轉

我們看一下小例子


算出m=2的兩個新特徵維度,為什麼取二呢?這就可能結合了業務場景,給出2
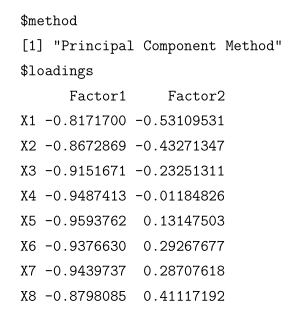
但是得出這組資料不好解釋,做正交旋轉


![]()
-------------------------------------------------------------------
但是我們有時候不能太相信主成分分析(就相當於不是萬能的),比如
y x1 x2
3 3 200
5 5 -1000
7 7 -399
1 1 400
我們看著組資料的話,顯然y=x1就已經是我們想要的了,但是假如使用主成分分析的話,主成分分析完全不考慮因變數,其發現x1這個特徵方差小,可能衍生出一個新特徵z1=0.99x1+0.1x2,這樣和我們想要的y=x1完全不搭了
應用




