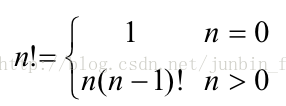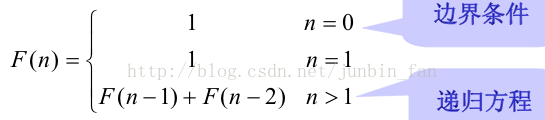一、遞迴的思想和定義

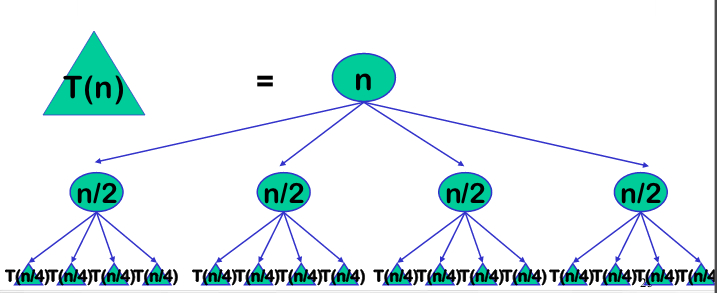
（一）、孫子兵法道：凡治眾如治寡，分數是也。在使用計算機解決問題時我們經常遇到的問題是規模較大的問題，不能直接求解，最普遍的方法就是分解問題。遞迴就是一種特殊的分治思想，在解決一個規模為n的大問題時，先將這個大問題分解為規模為k的與原問題在形式上相同且相互獨立的子問題，若子問題不夠小繼續分解直到子問題小到能直接解決為至，然後解決各個子問題，自底向上的合併各個子問題的解形成原問題的解。

（二）、直接或間接地呼叫自身的演算法稱為遞迴演算法 ，用函式自身給出定義的函式稱為遞迴函式 。 

二、常見的遞迴問題

1、n的階乘

#include <stdio.h>
//計算n! 
double factorial(double n)
{
	//邊界條件
	if(n==1)
		return 1;
	//遞迴方程
	else
		return n*factorial(n-1);
}

int main()
{
	int n;
	printf("please input n\n");
	scanf("%d",&n);
	printf("%d! =%.2f\n",n,factorial(n));
	return 0;
}
 

無窮數列1，1，2，3，5，8，13，21，34，55， … ，被稱為Fibonacci數列。它可以遞迴地定義為： 

#include <stdio.h>

//計算斐波那契數列的第n項 
double Fibonacci(int n){
	//邊界條件
	if(n<=2)
		return 1;
	//遞迴方程
	else
		return Fibonacci(n-1)+Fibonacci(n-2);
}

int main(){
	int n;
	printf("please input n \n"); 
	scanf("%d",&n);
	printf("Fibbnicc(%d) = %.2f\n",n,Fibonacci(n));
	return 0;
}
 

#include <stdio.h>
#define Length 5

//輸出R中所有元素
void printAllElement(int* R){
	int i;
	for(i = 0; i < Length; i++){
		printf("%d ",R[i]);
	}
	printf("\n");
}
//交換R[i],R[j]
void swap(int R[],int i, int j){
	int temp;
	temp = R[i];
	R[i] = R[j];
	R[j] = temp;
}

//遞迴排列 R[k]--R[m]中的(m-k+1)個元素 
void perm(int* R,int start,int finish){
	//邊界條件(R中只有一個元素)
	if(start == finish){
		printAllElement(R);
	}
	//遞迴方程
	else{
		//迴圈指定R中的每個元素ri
		for(int i = start; i < finish; i++){
			//通過交換R[i]/R[start]實現指定R[i]到首位置 
			swap(R,start,i);
			//對R中剩下的元素R(start+1,finish)進行排列
			perm(R,start+1,finish);
			//換回原位置
			swap(R,start,i);
		}
	}
}

int main(){
	int R[]={1,2,3,4,5};
	perm(R,0,5);
	return 0;
}
 

4、Hanoi塔問題

設有A、B、C三個塔座，起始時A上有n個圓盤（編號：1，2，3，...n）自項向下，由小到大排列。現要求把A上的n個圓盤移到到B上，並按原次序排列，移到過程中遵守以下三個規則：

• 規則一：每次只能移動1個圓盤；
• 規則二：任何時候都不允許大的圓盤壓住小的圓盤；
• 規則三：在滿足規則一、二的情況下可以移動到A、B、C任何一個塔座上。

void Hanoi(int n, int A, int B, int C)
{
	if(n>0)
	{
		//先把A上的前n-1個藉助B移動到C上
		Hanoi(n-1,A,C,B);
		//把A上的最下面的第n個移動到B
		move(A,B);
		//最後把C上的n-1個藉助A移動到B上
		Hanoi(n-1,C,B,A);	
	}
}

5、正整數的劃分

 將正整數n表示成一系列正整數之和：n=n1 +n2+ … +nk ，其中n1≥n2≥ … ≥nk≥1，k≥1，這種表示稱為正整數n的劃分。求正整數n的不同劃分個數。 

#include <stdio.h>

//遞迴求解正整數n的劃分數p(n)=q(n,n) 
int qIntegerDivision(int n,int m){
	
	//邊界條件 q(1,1)=1, (n=1,m=1) 
	if(n == 1 && m == 1){
		return 1;
	}
	
	//遞迴方程 q(n,n), (n<m) 
	if(n < m){
		return qIntegerDivision(n,n);
	}
	
	//遞迴方程 1+q(n,n-1), (n=m) 
	if(n == m){
		return 1 + qIntegerDivision(n,n-1);
	}
	
	//遞迴方程 q(n,m-1) + q(n-m,m), (n>m>1) 
	if(n > m && m > 1){
		return qIntegerDivision(n,m-1) + qIntegerDivision(n-m,m);
	}
}

int main(){
	int n,m;
	printf("please input n,m\n");
	scanf("%d,%d",&n,&m);
	printf("q(%d,%d)=%d\n",n,m,qIntegerDivision(n,m));
	return 0;
}

6、Ackerman函式

當一個函式及其它的變數是由函式自身定義時，稱這個函式是雙遞迴函式。

#include <stdio.h>

//Ackerman雙遞迴函式 
int ackerman(int n,int m){
	
	//邊界條件 A(1,0)=2 
	if(n == 0 && m == 1){
		return 0;
	}
	
	//邊界條件 A(0,m)=1, m>=0 
	if(n == 0 && m >= 0){
		return 1;
	}
	
	//邊界條件 A(n,0)=n+2, n>=2 
	if(n >= 2 && m == 0){
		return n + 2;
	}
	
	//遞迴方程 A(n,m)=A(A(n-1,m),m-1), n,m>=1 
	if(n >= 1 && m >= 1){
		return ackerman(ackerman(n-1,m),m-1);
	}
}

int main(){
	int n,m;
	printf("please input n,m\n");
	scanf("%d,%d",&n,&m);
	printf("A(%d,%d)=%d\n",n,m,ackerman(n,m));
	return 0;
}

三、遞迴優缺點

1、優點：結構清晰、設計簡單、容易實現，可用數學歸納法來證明它的正確性。

2、缺點：執行效率低，需要耗費大量的CPU時間和記憶體空間，尤其當遞迴變數n大到增大到一定程度時，這種低效率更為明顯。