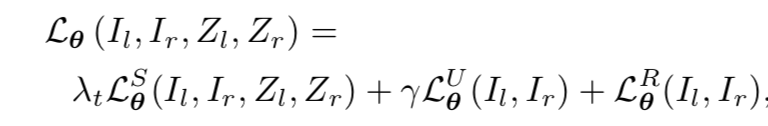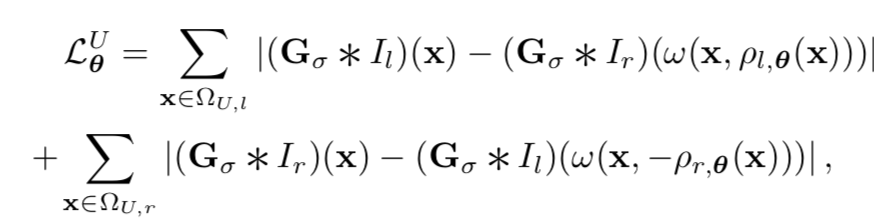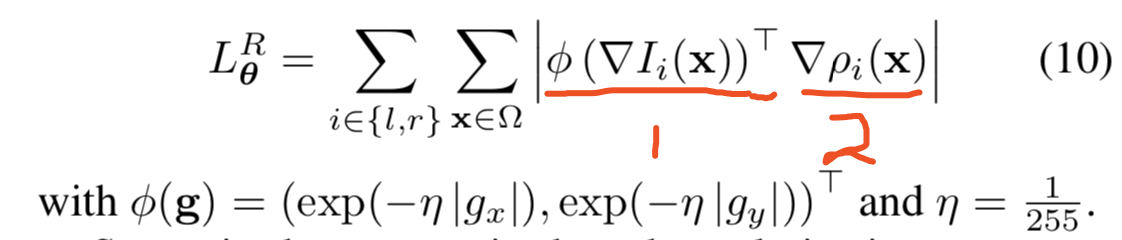論文筆記-深度估計(4) Semi-Supervised Deep Learning for Monocular Depth Map Prediction
CVPR2017_Semi-Supervised Deep Learning for Monocular Depth Map Prediction
這是一篇用雙目進行無監督學習估計深度的論文。
對一幅圖進行有監督訓練進行深度估計時,由於採集裝置的侷限,並非影象的每個畫素都有對應的真實值。於是作者提出在影象有真實值的地方進行監督學習,無真實值的地方進行無監督學習(最終作者發現對整個影象都進行無監督學習+部分地方有監督學習效果最好)。這樣的結合,使得無監督學習部分學習起來相對輕鬆甚至不需要很複雜的價值函式而不用擔心陷入區域性最優解,使得有監督學習速度能更快。
最後作者達到了state of art的效果。
1.介紹
作者認為當前有監督學習過程中過於依賴真實值,但真實值可能有以下問題:
- 有誤差和噪音;
- 雷達等真值採集的測量值很稀疏;
- 需要對影象系統的內外參進行標定。
- 相機和雷達不能很好地對準,特別是兩者中心無法很好對準,導致本來在相機視野之外的真值也投影到圖片中
2.價值函式
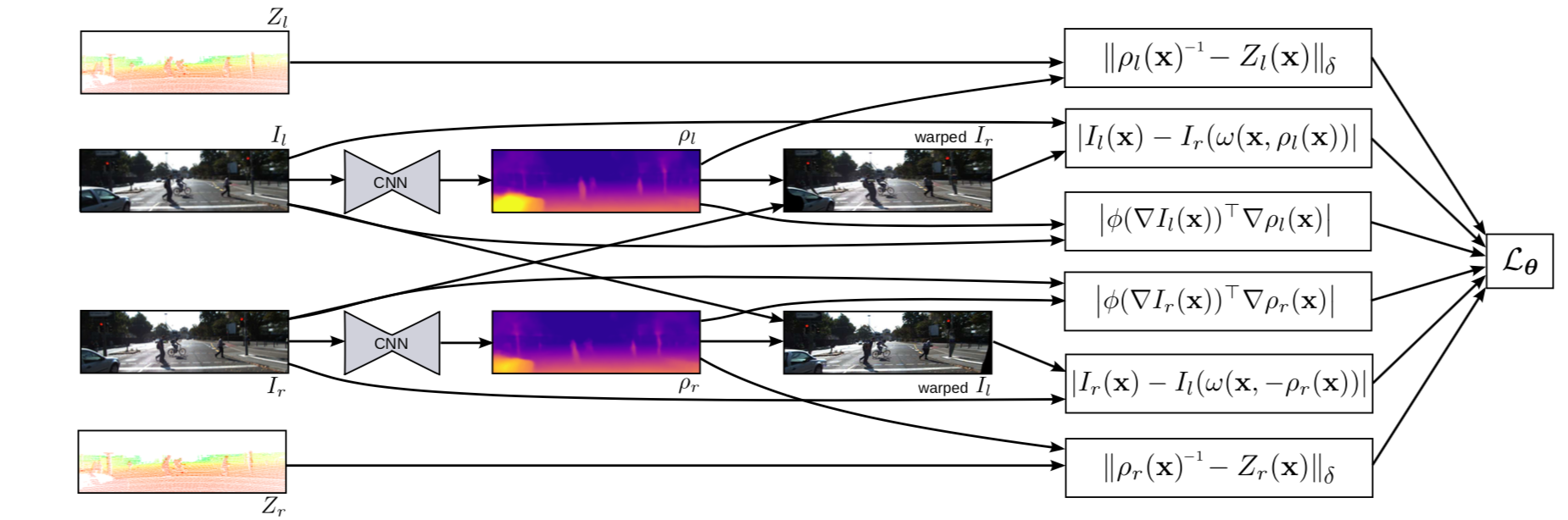
整體流程如圖:
相比前幾篇論文,此處作者以預測逆深度為目標。我們知道,整個深度的分佈由近及遠是一個長尾分佈,所以比起直接用深度Z,用反逆深度能更好地表達深度的數值特點。
作者總的價值函式包括有監督深度誤差,無監督深度誤差和正則化三個部分:
有時會感嘆,雙目匹配和深度估計在很長一段時間是高度相關的,深度估計也形成了形如雙目匹配中
2.1有監督誤差:
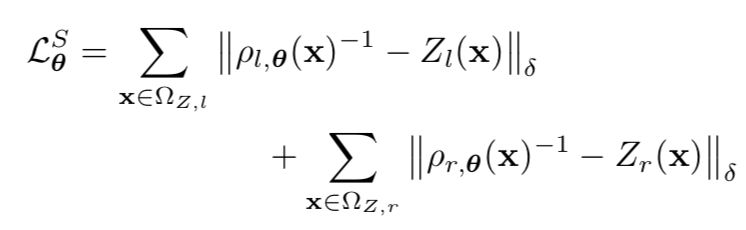
作者對用了一個Berhu函式(類似Huber)。我們知道Huber函式常用來抵消outlier對模型的損害,當某個outlier離模型過遠時,損失就有L2變為L1。而此處用Berhu函式是更希望快速壓制大的深度殘差,所以此處用Berhu函式:

其中大小為所有“真值-誤差”對中差異最大值的0.2倍。
2.2無監督深度誤差:
作者先對影象進行高斯平滑消除噪音,然後再利用雙目之間baseline,焦距等內外引數已知的情況下,分別將左檢視中的點投影到右檢視的誤差,以及將右檢視的點投影到左檢視的誤差一同納入誤差計算中。
2.3 正則項
作者採用類似於文章[1]的正則化,使得正則項兼有平滑深度變化,同時保持物體邊界深度的不連續性的功能:
作者對每個畫素對x和y方向取梯度,但眾所周知物體邊緣的梯度是不連續的,所以作者取自然指數倒數的函式作為權重,當梯度太大(即遇到邊緣)時權重就小(就不會強行降低邊緣上的梯度了)。上式部分1是權重,部分2是深度的梯度。
對於那些無真值資料且弱紋理的區域,估計深度是ill-posed問題,但正則化有助於很好地在這類區域中估計深度。
2.網路
作者沿用大家常用的encoder(sample)-decoder(unsample)方式.decoder部分用ImageNet上的ResetNet-50,但沒有最後的全連線層,畢竟不需要做細分類。卷積層隨機初始化。
隨後的decoder據說比較複雜,其naive版本如下:
和主流方法一樣,作者加上了skip的方法,除了第一層外,每層都融合了encoder的某一層。作者發現skip能顯著提高最後輸出的精確度,但不影響系統收斂。
實現細則
最後的實現中,作者完全隨機初始化所有的卷積層引數,這樣一來,最初的預測值(逆深度)接近於0,且無監督部分loss接近於0,有監督部分loss卻會很大。於是作者給有監督部分的loss乘上了一個fade-in數值,這個數值會隨著迭代次數慢慢變小。同時,對所有的卷積網路的weight加上一個weight decay=0.00004。當然dropout也不能少。然後訓練網路直到驗證集的loss開始上升就停止迭代。
除最後一層輸出外,每層都有batch normalization。RELU啟用函式。
作者最後的結論是在所有畫素上進行無監督學習要比僅僅在無真實值的地方進行無監督學習好,價值函式中用BerHu函式比L2函式好(後者在訓練集中表現更好但在測試集中就栽跟頭;很明顯,測試集中有更多outlier(此處的outlier是相對訓練集的資料分佈來說))。作者同時指出:高斯模糊加分,長skip加分。
最終表現如下:

總體看來,無監督和有監督的表現還是差別挺大,無監督學習任重道遠。但兩種模型各有優缺點,相容兩種優點的模型更可能發揮更好效果。作者提到,在0-80米範圍內,增加了無監督學習的模型表現更好,因為這個區域內的真值非常稀疏。