機器學習基石 (Machine Learning Foundations) 作業1 Q15-17的C++實現
阿新 • • 發佈:2019-01-07
大家好,我是Mac Jiang。今天和大家分享Coursera-臺灣大學-機器學習基石 (Machine Learning Foundations) -作業1的Q15-17題的C++實現。這部分作業的任務主要是寫一個PLA分類器,用於解決一個4維資料的分類問題。我的程式碼也許能較好的執行PLA演算法,但它不一定是最好最快的實現過程,如果各位博友有更好的思路,請留言聯絡,謝謝!希望我的部落格能給您帶來一些學習上的幫助!
其他解答請看彙總帖:http://blog.csdn.net/a1015553840/article/details/51085129
PLA是一種十分簡單,快速的分類演算法,有速度快、實現簡單的特點,特別適用於樣本是線性可分的情況。對於線性可分的樣本,PLA的實現過程為:
{
1.尋找w(t)的下一個錯誤分類點(x,y)(即sign(w(t)’*x)!=y);
2.糾正錯誤:w(t+1) = w(t) + y*x;
}until(每個樣本都無錯)
#include<fstream>
#include<iostream>
#include<vector>
using namespace std;
#define DEMENSION 5
double weight[DEMENSION];//權重值
int step = 0;//修改次數
int n = 0;//訓練樣本數
char *file = "training_data.txt";//讀取檔名
//儲存訓練樣本,input為x,output為y
struct record{
double input[DEMENSION];
int output;
};
//把記錄存在向量裡而不是存在結構體陣列內,這樣可以根據實際一項項新增 (3)實驗結果:

45次
2.第16題

(1)題意:由於樣本的排列順序不同,最終完成PLA分類的迭代次數也不同。這道題要求我們打亂訓練樣本的順序,進行2000次PLA計算,得到平均迭代次數。
在C++中自帶打亂順序的演算法:random_shuffle函式,在呼叫之前,需要#include
(2)實現:
#include<fstream>
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define DEMENSION 5
double weight[DEMENSION];//權重值
int step = 0;//修改次數
int totalStep = 0;
int n = 0;//訓練樣本數
char *file = "training_data.txt";//讀取檔名
//儲存訓練樣本,input為x,output為y
struct record{
double input[DEMENSION];
int output;
};
//把記錄存在向量裡而不是存在結構體陣列內,這樣可以根據實際一項項新增
vector<record> trainingSet;
//將資料讀入訓練樣本向量中
void getData(ifstream &datafile)
{
while(!datafile.eof())
{
record curRecord;
curRecord.input[0] = 1;
int i;
for(i = 1; i < DEMENSION; i++){
datafile>>curRecord.input[i];
}
datafile>>curRecord.output;
trainingSet.push_back(curRecord);
}
datafile.close();
n = trainingSet.size();
}
//計算sign值
int sign(double x){
if(x <= 0)return -1;
else return 1;
}
//兩向量相加(實際為陣列相加),將結果儲存在第一個陣列內,用於計算w(i+1)=w(i)+y*x
void add(double *v1,double *v2,int demension){
int i;
for(i = 0;i < demension; i++)v1[i] += v2[i];
}
//計算兩數值相乘值,用於判斷w*x是否小於0,若小於0要執行修正演算法
double multiply(double *v1,double *v2,int demension){
double temp = 0.0;
int i;
for(i = 0; i < demension; i++)temp += v1[i] * v2[i];
return temp;
}
//計算實數num與向量乘積放在result中,用於計算y*x
void multiply(double *result,double *v,int demension,double num){
int i;
for(i = 0; i < demension; i++)result[i] = num * v[i];
}
void PLA()
{
int correctNum = 0;//當前連續正確樣本數,當等於n則表明輪完一圈,則表示全部正確,演算法結束
int index = 0;//當前正在計算第幾個樣本
bool isFinished = 0;//演算法是否全部完成的表示,=1表示演算法結束
while(!isFinished){
if(trainingSet[index].output == sign(multiply(weight,trainingSet[index].input,DEMENSION)))correctNum++;//當前樣本無錯,連續正確樣本數+1
else{//出錯,執行修正演算法
double temp[DEMENSION];
multiply(temp,trainingSet[index].input,DEMENSION,trainingSet[index].output);//計算y*x
add(weight,temp,DEMENSION);//計算w(i+1)=w(i)+y*x
step++;//進行一次修正,修正次數+1
correctNum = 0;//由於出錯了,連續正確樣本數歸0
//cout<<"step"<<step<<":"<<endl<<"index="<<index<<" is wrong"<<endl;
}
if(index == n-1)index = 0;
else index++;
if(correctNum == n)isFinished = 1;
}
}
void main()
{
ifstream dataFile(file);
if(dataFile.is_open()){
getData(dataFile);
}
else{
cout<<"出錯,檔案開啟失敗!"<<endl;
exit(1);
}
int i;
for(i = 0; i < 2000; i++)
{
random_shuffle(trainingSet.begin(), trainingSet.end());
int j;
for(j = 0; j < DEMENSION; j++)weight[j] = 0.0;
PLA();
totalStep += step;
cout<<"第"<<i<<"次迭代的step:"<<step<<endl;
step = 0;
}
cout<<"average step:"<<totalStep/2000<<endl;
}(3)實驗結果:
平均40次
3.第17題
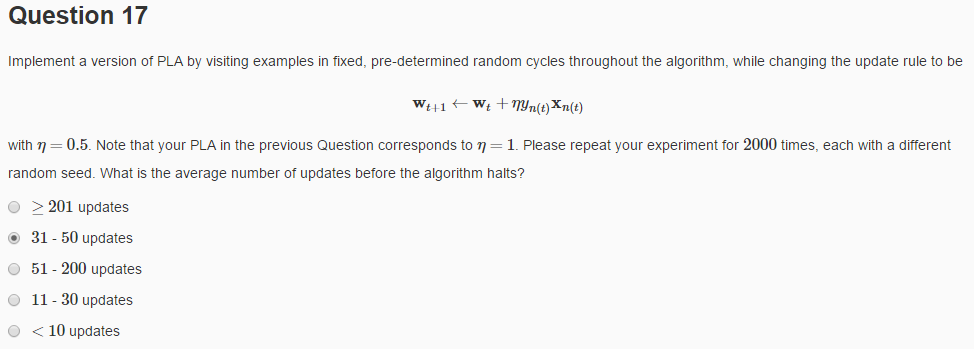
這道題實現更加簡單,只要在num之前*0.5就可以了
void multiply(double *result,double *v,int demension,double num){
int i;
for(i = 0; i < demension; i++)result[i] = num * v[i];
}
大約為40次
