Dijkstra（迪傑斯特拉）是一個非常基礎的演算法，也是最常用的，被用於求解圖論的最短路問題。但看網上好多教程都寫的很複雜，我爭取用最易懂的對新手友好的語言來解釋清楚這個演算法。

使用範圍

求解有向帶邊權圖的最短路問題，給定起點，給定邊權和起止點，求到達每一個點的最短距離。

演算法概述

從起點（由輸入給出）開始，遍歷所有的和起點直接相連的點，比如現在我們假設1號是起點。

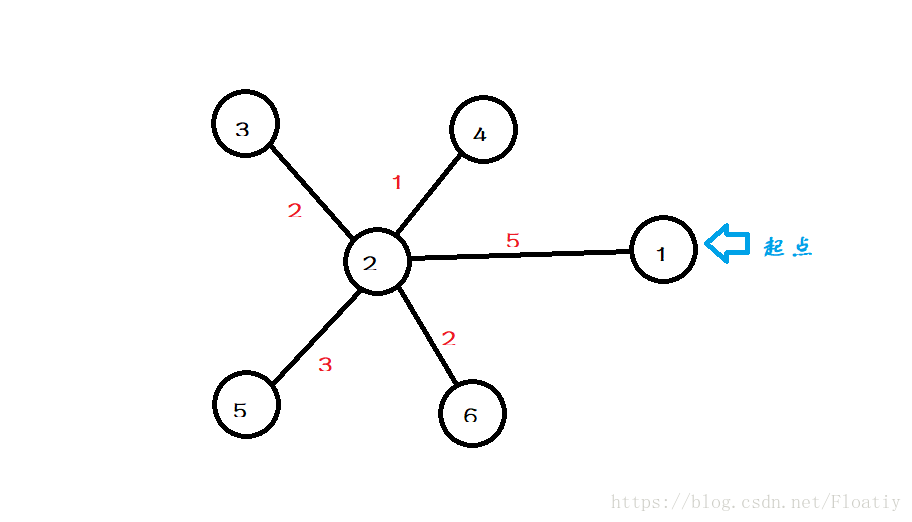
拿上面這張圖舉例子
首先，把除了起點以外的點的距離都初始化為無限大(INF)（i到起點距離用dist[i]表示）

dist[1] 0
dist[2] INF
dist[3] INF
dist[4]
 
 INF
dist[5] INf
dist[6] INF

和1直接相連的點是2，那麼我們現在把2到起點的距離處理一下，應該是5

dist[1] 0
dist[2] 5
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF

以此類推，每次把與 已確定距離的點 相連的點的dist值處理一下就好了
最後我們可以得到下面這張表：

dist[1] 0
dist[2] 5
dist[3] 5+2=7
dist[4] 5+1=6
dist[5] 5+3=8
dist[6] 5+2=7

看上去你已經理解Dijkstra演算法的大體思路了，看上去很簡單，任何困難的事情都是一點一點做成的。

那麼，如果我的圖變成這樣呢？
我可沒有保證沒有環

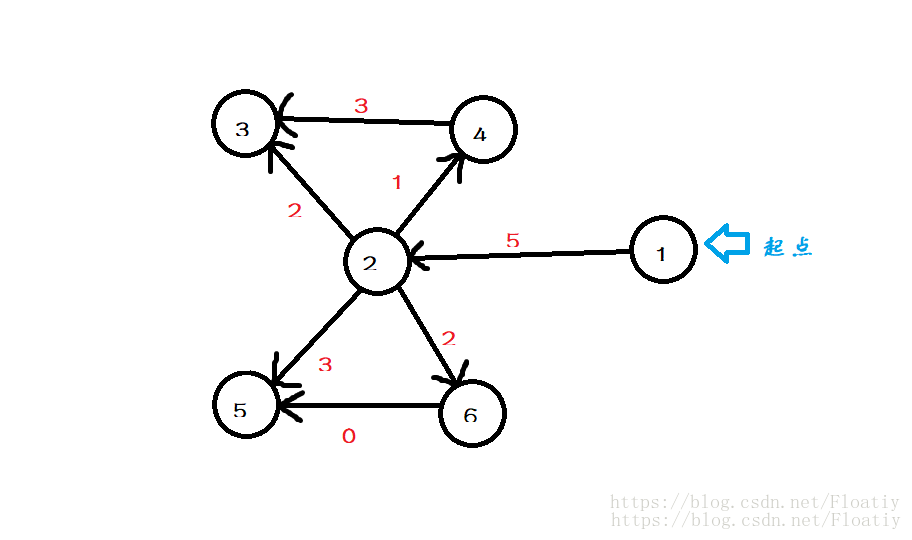
我加了幾條邊，產生了環，（沒錯那條邊邊權就是0）
這樣帶來的問題就是，每一個點將會有不止一種方法到達。
那我們到底應該怎麼辦？很簡單啊，選到達方式中最優的方案。
我再來手動模擬一下，，，（前半部分和前一個例子相同)

[重點]每一次處理一個點（簡稱 這個點）時，我們需要列舉它可以到達的點（簡稱 那個點）的dist值，如果當前算出的距離比那個點原來記錄下來的dist值小，就把那個點的dist賦值成當前算出的那個點到起點的距離。

首先，把除了起點以外的點的距離都初始化為無限大(INF)（i到起點距離用dist[i]表示）
我們再引入一個叫vis的陣列來記錄一個點是否被處理過

dist[1] 0
dist[2] INF
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF

和1直接相連的點是2，那麼我們現在把2到起點的距離處理一下，應該是5

dist[1] 0
dist[2] 5
dist[3] INF
dist[4] INF
dist[5] INf
dist[6] INF

這時候就不同了，我們可以看到，2號點連著4條邊，這時

Dijkstra演算法要求我們從中按到起點距離的大小 從小到大依次處理這些點。

so，我們應該處理4號點了，這樣的話，可以得到下表

dist[1] 0
dist[2] 5
dist[3] dist[4]+3=9
dist[4] dist[2]+1=6
dist[5] INF
dist[6] INF

按順序，我們處理完4號點該處理3號點了，但我們發現3號點已經有dist值了（9），但我們現在計算出來3號點距離應該是dist[2]+2=7，比原來的要優，所以我們將dist[3]賦值為7。這個操作叫“更新”。
那麼我們就可以依次將所有點處理完了。
最後得到：

dist[1] 0
dist[2] 5
dist[3] 7
dist[4] 6
dist[5] 7
dist[6] 7

那麼，現在你已經理解了基礎的Dijkstra了。

code

//by floatiy
#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
//別問我為什麼用longlong 這是洛谷的單源最短路的模板
const long long INF=2147483647;
const int MAXN=10000;
const int MAXM=500000;
int n,m,s;//n個點 m條邊 從第s號點開始
int node;//當前正在處理的節點
long long minn;
long long dist[MAXN];//每個點到起點的距離
bool vis[MAXN];//是否處理過
struct Edge{//邊的結構體 
    int w;//邊權
    int pre,to;//pre是出發點 to是終點 這個是有向邊
}l[MAXM];
struct Node{//節點的結構體
    int num;//以這個點為起點的邊的個數
    vector<int> about;//利用stl存以這個點為起點的邊的編號，不知道的就把ta當成動態陣列吧
}a[MAXN];
int find_new()//每次處理完找新節點的函式
{
    for(int i=1;i<=n;i++)//找新的開始點 
    {
        if(vis[i]==0 && minn>dist[i])//從沒有處理過的點裡找離起點最近的進行處理
        {
            minn=dist[i];//貪心找最小
            node=i;//node其實就是下一步要被處理的點的編號
        }
    }
}
long long min_(long long x,long long y)//手寫min函式更快~
{
    return x>y?x:y;
}
int main()
{
    cin>>n>>m>>s;
    for(int i=1;i<=n;i++)
    {
        dist[i]=INF;//初始化 所有點到起點的距離設成無限大
//      cout<<dist[i]<<endl;//DEBUG
    }
    int x,y,z;
    for(int i=1;i<=m;i++)//輸入邊
    {
        scanf("%d%d%d",&x,&y,&z);//依次是 起點 終點 邊權
        l[i].pre=x,l[i].to=y;
        l[i].w=z;
        a[x].num++;//起點的出度+1
        a[x].about.push_back(i);//記錄這個邊
    }
    dist[s]=0;//起點距離設成0
    node=s;//從起點開始處理
    while(!vis[node])
    {
        vis[node]=1;//已經處理過了
        minn=INF;//每次記得讓minn變成無限大
        //這裡比較難懂,因為我奇怪的雙結構體存圖方法，我不會前向星。。。
        //總之下面這個迴圈就是列舉一下每一條從node節點出去的邊，然後處理它們所連的點的dist
        for(int i=0;i<a[node].num;i++)//列舉每條從這個點出去的邊在這個點的所有出邊中的編號i
        {
            if(dist[l[  a[node].about[i]  ].to] > dist[node]+l[  a[node].about[i]  ].w)
            //如果出邊連到的那個點到起點的距離
            //比
            //現在這個點到起點的距離+這條邊的邊權
            //要大
            //我們就更新連到的這個點的dist值
                dist[l[  a[node].about[i]  ].to]=dist[node]+l[  a[node].about[i]  ].w;
        }
        node=find_new();//做完一個點，找下一個點
    }
    for(int i=1;i<=n;i++)
        printf("%d ",dist[i]);
}

大家儘量去理解，我這個雙結構體真的不好理解，建議大家換一種存圖的方法。
我太弱了qwq，不會前向星。

堆優化介紹

大家想想，上面的程式有哪裡可以大幅度節約時間呢？
每個點的處理是必要的
輸入輸出也找不到能大幅度降低時間複雜度的辦法
那麼？

沒錯，在我們查詢新節點的時候，採取的是將每個點都列舉一遍的辦法，顯然這樣會讓時間複雜度變成n^2，但我們有一個叫堆的好東西，emmm如果不知道堆排序可以看一下這個，原理很簡單的：堆排序
我們建一個小根堆，這樣就能很方便的在nlogn的時間內找出最小值了
或者。。如果懶的話可以用一個東西，叫優先佇列（STL裡的priority_queue）
寫一份程式碼：
這個是在上一份程式碼的基礎上改的，故不加備註了，stl的友元函式過載我也不是很懂，，，大家可以baidu一下。。。

//Dijkstra 堆優化 
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int MAXN=1005;
const int MAXM=100005;
const int INF=0xfffffff;
int n,m,s;
struct Edge{
    int to;
    int next;
    int w;
}l[MAXM];
int head[MAXN],cnt;
int dis[MAXN];
bool vis[MAXN];
struct Node{
    int no;
    int dis;
    friend bool operator < (Node x,Node y)
    {
        return x.dis < y.dis;
    }
}a[MAXN];
priority_queue<Node> q;
void add(int x,int y,int z)
{
    cnt++;
    l[cnt].to=y;
    l[cnt].w=z;
    l[cnt].next=head[x];
    head[x]=cnt;
}
int main()
{
    cin>>n>>m>>s;
    int x,y,z;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
    }
    for(int i=1;i<=n;i++) a[i].dis=INF,a[i].no=i;
    a[s].dis=0;
    q.push(a[s]);//忘了扔起點 出鍋*1 
    int cur=s;
    while(!q.empty())
    {
        cur=q.top().no;
        q.pop();
        if(vis[cur]) continue;//注意是看cur是否處理過，而非看to是否處理過 出鍋*2 
        vis[cur]=1;
        for(int i=head[cur];i;i=l[i].next)
        {
            if(a[l[i].to].dis > a[cur].dis+l[i].w)
            {
                a[l[i].to].dis=a[cur].dis+l[i].w;
                q.push(a[l[i].to]);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        printf("%d : %d\n",i,a[i].dis);
    }
    return 0;
}