二叉樹前序、中序、後序遞迴與非遞迴遍歷+層序遍歷(java)
阿新 • • 發佈:2019-01-07
前序遞迴遍歷演算法:訪問根結點-->遞迴遍歷根結點的左子樹-->遞迴遍歷根結點的右子樹
中序遞迴遍歷演算法:遞迴遍歷根結點的左子樹-->訪問根結點-->遞迴遍歷根結點的右子樹
後序遞迴遍歷演算法:遞迴遍歷根結點的左子樹-->遞迴遍歷根結點的右子樹-->訪問根結點
層序遍歷演算法:將每個節點放入佇列中。依據佇列先進先出的特點,順序遍歷樹。直到佇列為空
二叉樹為:
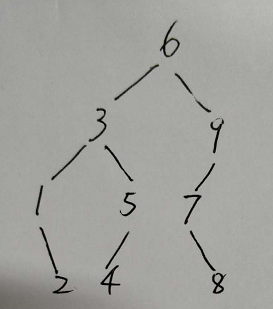
Java程式碼:
二叉樹節點定義Treel.java:
package Test_1; public class TreeNode { int data; TreeNode left; TreeNode right; public TreeNode(){}; TreeNode(int data,TreeNode left, TreeNode right){ super();//千萬別忘了,不然會出錯,如果沒有這句在node9例項化時報錯 this.data = data; this.left = left; this.right = right; } public int getData(){ return data; } public void setData(int data){ this.data = data; } public TreeNode getLeft(){ return left; } public void setLeft(TreeNode left){ this.left = left; } public TreeNode getRight(){ return right; } public void setRight(TreeNode right){ this.right = right; } }
二叉樹遍歷實現程式碼BinaryTree.java:
package Test_1; import java.util.LinkedList; import java.util.Queue; import java.util.Stack; public class BinaryTree { //前序遞迴實現 public void preOrderRe(TreeNode root){ //System.out.println(biTree.value); if(root != null){ System.out.print(root.getData()+", "); preOrderRe(root.getLeft()); preOrderRe(root.getRight()); } } //前序非遞迴的方式 public void preOrderNonRecursive(TreeNode root){ Stack<TreeNode> stack = new Stack<>(); while(true){ while(root !=null){ System.out.print(root.getData()+", "); stack.push(root); root = root.getLeft(); } if(stack.isEmpty()) break;//遍歷完最後一個節點時呼叫這一句跳出迴圈 root = stack.pop(); root = root.getRight(); } } //中序遍歷+遞迴 public void inOrder(TreeNode root){ if(root != null){ inOrder(root.getLeft()); System.out.print(root.getData()+", "); inOrder(root.getRight()); } } //中序遍歷+非遞迴 public void inOrderNonRecursive(TreeNode root){ Stack<TreeNode> stack = new Stack<>(); while(true){ while(root != null){ stack.push(root); root = root.getLeft(); } if(stack.isEmpty()) break; root = stack.pop(); System.out.print(root.getData()+", "); root = root.getRight(); } } //後序遍歷+遞迴 public void postOrder(TreeNode root){ if(root != null){ postOrder(root.getLeft()); postOrder(root.getRight()); System.out.print(root.getData()+", "); } } //後續遍歷+非遞迴(這是最難的一個) //主要思想:首先遍歷root根節點的所有左節點,並依次入棧。對出棧的元素,如果沒有右兒子或者 //雖然有右兒子但右兒子已完成遍歷,即可完成出棧;否則,再次入棧,並把右兒子入棧,遍歷右 //兒子的所有左兒子。 //後序遍歷的難點在於:需要判斷上次訪問的節點是位於左子樹,還是右子樹。若是位於左子樹, //則需跳過根節點,先進入右子樹,再回頭訪問根節點;若是位於右子樹,則直接訪問根節點。 public void postOrderNonRecursive(TreeNode root){ Stack<TreeNode> stack = new Stack<>(); while(true){ if(root !=null){ stack.push(root); root = root.getLeft(); }else{ if(stack.isEmpty()) return; if(stack.lastElement().getRight() == null){//Vector中lastElement(),Returns the last component of the vector. root = stack.pop(); System.out.print(root.getData()+", "); while(root == stack.lastElement().getRight()){ System.out.print(stack.lastElement().getData()+", "); root = stack.pop(); if(stack.isEmpty()){ break; } } } if(!stack.isEmpty()) root = stack.lastElement().getRight(); else root = null; } } } //層序遍歷 /*offer,add區別: * 一些佇列有大小限制,因此如果想在一個滿的佇列中加入一個新項,多出的項就會被拒絕。 這時新的offer 方法 * 就可以起作用了。它不是對呼叫 add() 方法丟擲一個 unchecked 異常,而只是得到由 offer() 返回的 false。 * poll,remove區別: * remove() 和 poll() 方法都是從佇列中刪除第一個元素。remove() 的行為與 Collection 介面的版本相似, * 但是新的 poll() 方法在用空集合呼叫時不是丟擲異常,只是返回 null。因此新的方法更適合容易出現異常條件的情況。 */ public void levelOrder(TreeNode root){ TreeNode temp; Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); while(!queue.isEmpty()){ temp = queue.poll(); System.out.print(temp.getData()+", "); if(temp.getLeft() != null) queue.offer(temp.getLeft()); if(temp.getRight() != null) queue.offer(temp.getRight()); } } public static void main(String[] args) { //注意如果建立使用函式二叉樹,則必須逆序建立,先建立子節點,再逆序往上建立,因為非葉子結點會使用到下面的節點, //而初始化是按順序初始化的,不逆序建立會報錯;如果不適用函式建立二叉樹,像下面這樣做,不必用逆序建立 TreeNode node9 = new TreeNode(8,null, null); TreeNode node8 = new TreeNode(4,null, null); TreeNode node7 = new TreeNode(2, null, null); TreeNode node6 = new TreeNode(7,null, node9); TreeNode node5 = new TreeNode(5,node8, null); TreeNode node4 = new TreeNode(1, null, node7); TreeNode node3 = new TreeNode(9, node6, null); TreeNode node2 = new TreeNode(3, node4, node5); TreeNode node1 = new TreeNode(6, node2,node3); BinaryTree tree = new BinaryTree(); System.out.println("先序遍歷二叉樹(遞迴):"); tree.preOrderRe(node1); System.out.println(); System.out.println("先序遍歷二叉樹(非遞迴):"); tree.preOrderNonRecursive(node1); System.out.println(); System.out.println("中序遍歷二叉樹(遞迴):"); tree.inOrder(node1); System.out.println(); System.out.println("中序遍歷二叉樹(非遞迴):"); tree.inOrderNonRecursive(node1); System.out.println(); System.out.println("後序遍歷二叉樹(遞迴):"); tree.postOrder(node1); System.out.println(); System.out.println("後序遍歷二叉樹(非遞迴):"); tree.postOrderNonRecursive(node1); System.out.println(); System.out.println("層序遍歷二叉樹(遞迴):"); tree.levelOrder(node1); System.out.println(); } }
執行結果:

