一、實驗目標

用GPU加速FFT程式執行，測量加速前後的執行時間，確定加速比。

二、實驗要求

• 採用CUDA或OpenCL（視具體GPU而定）編寫程式
• 根據自己的機器配置選擇合適的輸入資料大小 n
• 對測量結果進行分析，確定使用GPU加速FFT程式得到的加速比
• 回答思考題，答案加入到實驗報告敘述中合適位置

三、實驗內容

使用CUDA進行FFT加速

使用到的程式碼如下

• FFT.h

• typedef struct complex //複數型別
  {
  	float real;		//實部
  	float imag;		//虛部
  }complex;
  
  #define PI 3.1415926535
  
  void complex_plus(complex a, complex b, complex *c);//複數加
  void complex_mul(complex a, complex b, complex *c);//複數乘
  void complex_sub(complex a, complex b, complex *c);	//複數減法
  void complex_div(complex a, complex b, complex *c);	//複數除法
  void complex_abs(complex f[], float out[], float n);//複數陣列取模
  
  void fft(int N, complex f[]);//傅立葉變換 輸出也存在陣列f中
  void ifft(int N, complex f[]); // 傅立葉逆變換
  
  void conjugate_complex(int n, complex in[], complex out[]);
   
  

   

• CUDA.h

• #include "FFT.h"
  #include <iostream>
  #include <time.h>
  #include "cuda_runtime.h"
  #include "device_launch_parameters.h"
  #include "../include/cufft.h"
  
  #define NX 4096 // 有效資料個數
  #define N  5335// 補0之後的資料長度
  #define MAX 1<<12
  #define BATCH 1
  #define BLOCK_SIZE 1024
  using std::cout;
  using std::endl;
  
  complex m[MAX], l[MAX];
  
  bool IsEqual(cufftComplex *idataA, cufftComplex *idataB, const long int size)
  {
  	for (int i = 0; i < size; i++)
  	{
  		if (abs(idataA[i].x - idataB[i].x) > 0.000001 || abs(idataA[i].y - idataB[i].y) > 0.000001)
  			return false;
  	}
  
  	return true;
  }
  
  
  
  /**
  * 功能：實現 cufftComplex 陣列的尺度縮放，也就是乘以一個數
  * 輸入：idata 輸入陣列的頭指標
  * 輸出：odata 輸出陣列的頭指標
  * 輸入：size 陣列的元素個數
  * 輸入：scale 縮放尺度
  */
  static __global__ void cufftComplexScale(cufftComplex *idata, cufftComplex *odata, const long int size, float scale)
  {
  	const int threadID = blockIdx.x * blockDim.x + threadIdx.x;
  
  	if (threadID < size)
  	{
  		odata[threadID].x = idata[threadID].x * scale;
  		odata[threadID].y = idata[threadID].y * scale;
  	}
  }
  
  
  void conjugate_complex(int n, complex in[], complex out[])
  {
  	int i = 0;
  	for (i = 0; i < n; i++)
  	{
  		out[i].imag = -in[i].imag;
  		out[i].real = in[i].real;
  	}
  }
  
  void complex_abs(complex f[], float out[], int n)
  {
  	int i = 0;
  	float t;
  	for (i = 0; i < n; i++)
  	{
  		t = f[i].real * f[i].real + f[i].imag * f[i].imag;
  		out[i] = sqrt(t);
  	}
  }
  
  
  void complex_plus(complex a, complex b, complex *c)
  {
  	c->real = a.real + b.real;
  	c->imag = a.imag + b.imag;
  }
  
  void complex_sub(complex a, complex b, complex *c)
  {
  	c->real = a.real - b.real;
  	c->imag = a.imag - b.imag;
  }
  
  void complex_mul(complex a, complex b, complex *c)
  {
  	c->real = a.real * b.real - a.imag * b.imag;
  	c->imag = a.real * b.imag + a.imag * b.real;
  }
  
  void complex_div(complex a, complex b, complex *c)
  {
  	c->real = (a.real * b.real + a.imag * b.imag) / (b.real * b.real + b.imag * b.imag);
  	c->imag = (a.imag * b.real - a.real * b.imag) / (b.real * b.real + b.imag * b.imag);
  }
  
  #define SWAP(a,b)  tempr=(a);(a)=(b);(b)=tempr
  
  void Wn_i(int n, int i, complex *Wn, char flag)
  {
  	Wn->real = cos(2 * PI*i / n);
  	if (flag == 1)
  		Wn->imag = -sin(2 * PI*i / n);
  	else if (flag == 0)
  		Wn->imag = -sin(2 * PI*i / n);
  }
  
  //傅立葉變化
  void fft(int NN, complex f[])
  {
  	complex t, wn;//中間變數
  	int i, j, k, m, n, l, r, M;
  	int la, lb, lc;
  	/*----計算分解的級數M=log2(N)----*/
  	for (i = NN, M = 1; (i = i / 2) != 1; M++);
  	/*----按照倒位序重新排列原訊號----*/
  	for (i = 1, j = NN / 2; i <= NN - 2; i++)
  	{
  		if (i < j)
  		{
  			t = f[j];
  			f[j] = f[i];
  			f[i] = t;
  		}
  		k = NN / 2;
  		while (k <= j)
  		{
  			j = j - k;
  			k = k / 2;
  		}
  		j = j + k;
  	}
  
  	/*----FFT演算法----*/
  	for (m = 1; m <= M; m++)
  	{
  		la = pow(2, m); //la=2^m代表第m級每個分組所含節點數		
  		lb = la / 2;    //lb代表第m級每個分組所含碟形單元數
  					 //同時它也表示每個碟形單元上下節點之間的距離
  		/*----碟形運算----*/
  		for (l = 1; l <= lb; l++)
  		{
  			r = (l - 1)*pow(2, M - m);
  			for (n = l - 1; n < NN - 1; n = n + la) //遍歷每個分組，分組總數為N/la
  			{
  				lc = n + lb;  //n,lc分別代表一個碟形單元的上、下節點編號     
  				Wn_i(NN, r, &wn, 1);//wn=Wnr
  				complex_mul(f[lc], wn, &t);//t = f[lc] * wn複數運算
  				complex_sub(f[n], t, &(f[lc]));//f[lc] = f[n] - f[lc] * Wnr
  				complex_plus(f[n], t, &(f[n]));//f[n] = f[n] + f[lc] * Wnr
  			}
  		}
  	}
  }
  
  //傅立葉逆變換
  void ifft(int NN, complex f[])
  {
  	int i = 0;
  	conjugate_complex(NN, f, f);
  	fft(NN, f);
  	conjugate_complex(NN, f, f);
  	for (i = 0; i < NN; i++)
  	{
  		f[i].imag = (f[i].imag) / NN;
  		f[i].real = (f[i].real) / NN;
  	}
  }
  
  bool IsEqual2(complex idataA[], complex idataB[], const int size)
  {
  	for (int i = 0; i < size; i++)
  	{
  		if (abs(idataA[i].real - idataB[i].real) > 0.000001 || abs(idataA[i].imag - idataB[i].imag) > 0.000001)
  			return false;
  	}
  
  	return true;
  }
   
  

   

• Main

• int main()
  {
  	cufftComplex *data_dev; // 裝置端資料頭指標
  	cufftComplex *data_Host = (cufftComplex*)malloc(NX*BATCH * sizeof(cufftComplex)); // 主機端資料頭指標
  	cufftComplex *resultFFT = (cufftComplex*)malloc(N*BATCH * sizeof(cufftComplex)); // 正變換的結果
  	cufftComplex *resultIFFT = (cufftComplex*)malloc(NX*BATCH * sizeof(cufftComplex)); // 先正變換後逆變換的結果
  
  	// 初始資料
  	for (int i = 0; i < NX; i++)
  	{
  		data_Host[i].x = float((rand() * rand()) % NX) / NX;
  		data_Host[i].y = float((rand() * rand()) % NX) / NX;
  	}
  
  
  	dim3 dimBlock(BLOCK_SIZE); // 執行緒塊
  	dim3 dimGrid((NX + BLOCK_SIZE - 1) / dimBlock.x); // 執行緒格
  
  	cufftHandle plan; // 建立cuFFT控制代碼
  	cufftPlan1d(&plan, N, CUFFT_C2C, BATCH);
  
  	// 計時
  	clock_t start, stop;
  	double duration;
  	start = clock();
  
  	cudaMalloc((void**)&data_dev, sizeof(cufftComplex)*N*BATCH); // 開闢裝置記憶體
  	cudaMemset(data_dev, 0, sizeof(cufftComplex)*N*BATCH); // 初始為0
  	cudaMemcpy(data_dev, data_Host, NX * sizeof(cufftComplex), cudaMemcpyHostToDevice); // 從主機記憶體拷貝到裝置記憶體
  
  	cufftExecC2C(plan, data_dev, data_dev, CUFFT_FORWARD); // 執行 cuFFT，正變換
  	cudaMemcpy(resultFFT, data_dev, N * sizeof(cufftComplex), cudaMemcpyDeviceToHost); // 從裝置記憶體拷貝到主機記憶體
  
  	cufftExecC2C(plan, data_dev, data_dev, CUFFT_INVERSE); // 執行 cuFFT，逆變換
  	cufftComplexScale << <dimGrid, dimBlock >> > (data_dev, data_dev, N, 1.0f / N); // 乘以係數
  	cudaMemcpy(resultIFFT, data_dev, NX * sizeof(cufftComplex), cudaMemcpyDeviceToHost); // 從裝置記憶體拷貝到主機記憶體
  
  	stop = clock();
  	duration = (double)(stop - start) * 1000 / CLOCKS_PER_SEC;
  	cout << "FFT經過GPU加速之後的時間為" << duration << "ms" << endl;
  
  	cufftDestroy(plan); // 銷燬控制代碼
  	cudaFree(data_dev); // 釋放空間
  
  
  	if (IsEqual(data_Host, resultIFFT, NX))
  		cout << "逆變化檢測通過。" << endl;
  	else
  		cout << "逆變換檢測不通過。" << endl;
  
  
  
  	//cpu fft
  	for (long int i = 0; i < MAX; i++) {
  		m[i].real = float((rand() * rand()) % 4096) / 4096;
  		l[i].real = m[i].real;
  		l[i].imag = m[i].imag = 0;
  	}
  	clock_t start2, end2;
  	double duration1;
  	start2 = clock();
  	fft(MAX, m);
  	ifft(MAX, m);
  	end2 = clock();
  	duration1 = (double)(end2 - start2) * 1000 / CLOCKS_PER_SEC;
  	cout << "FFT經過CPU加速之後的時間為 " << duration1 << " ms" << endl;
  
  	if (IsEqual2(m, l, MAX))
  		cout << "逆變化檢測通過。" << endl;
  	else
  		cout << "逆變化檢測不通過。" << endl;
  
  	return 0;
  }
   
  

  ---

   

四、測試平臺

• CPU：i7-6500U

• GPU：NVIDA GTX960M

• 記憶體：DDR3 8GB

• 作業系統：Windows 10 專業版

• 編譯器：Microsoft Visual Studio Enterprise 2017

五、測試記錄

分別測試資料集2^14、2^15、2^16、2^17、2^18時的執行情況

2^14

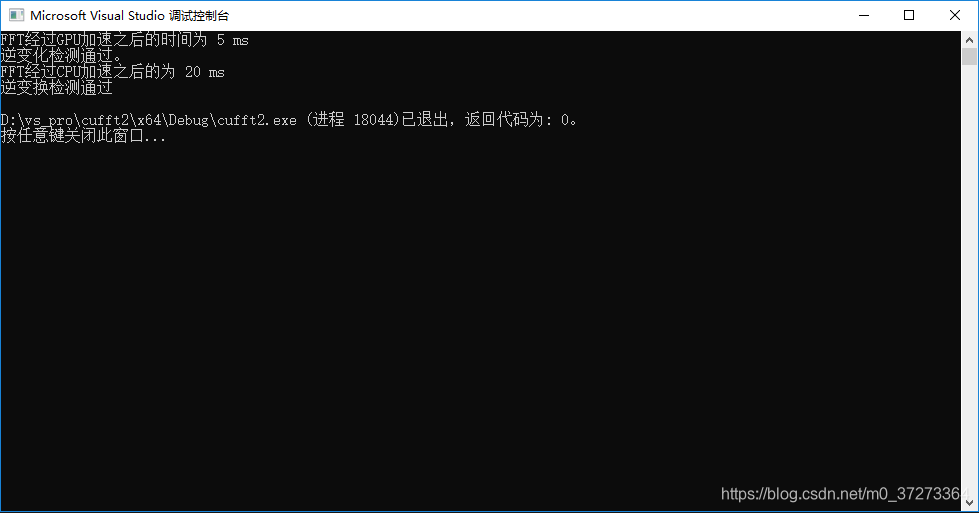
2^15

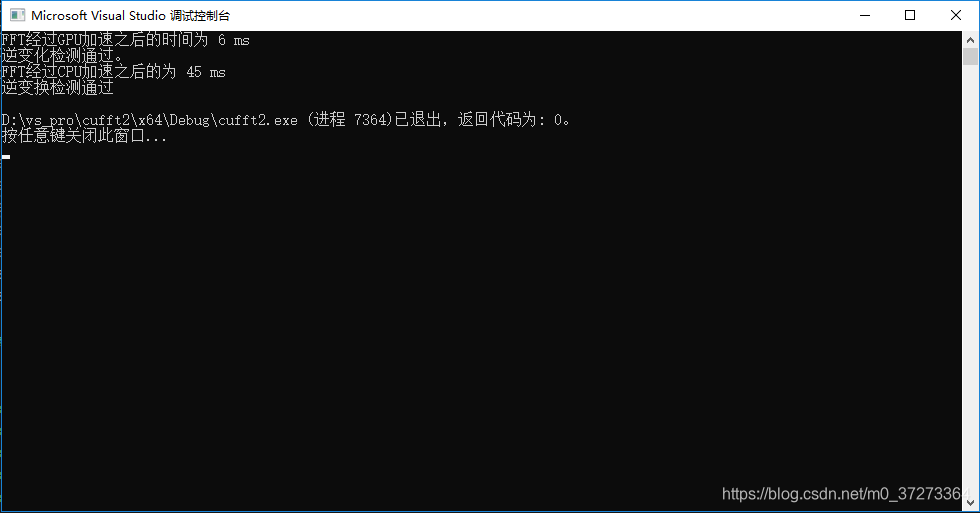
2^16

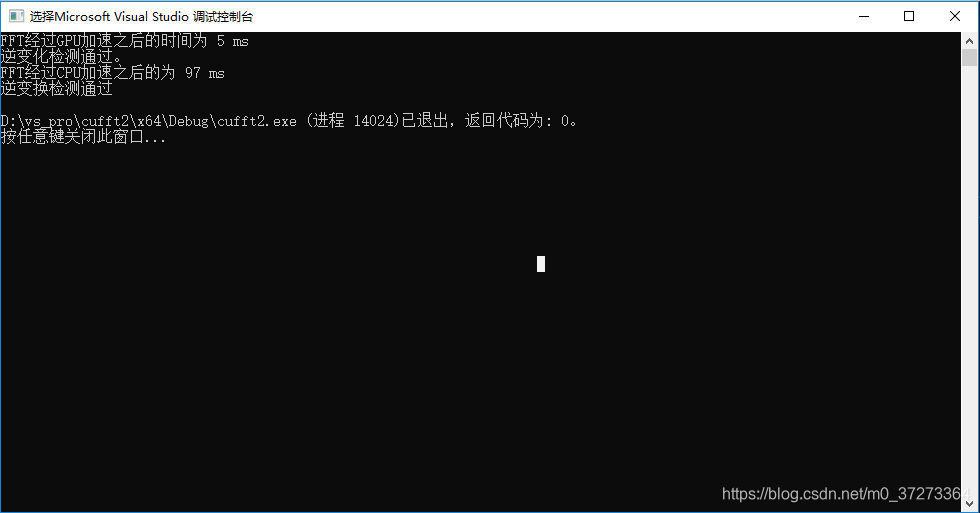
2^17

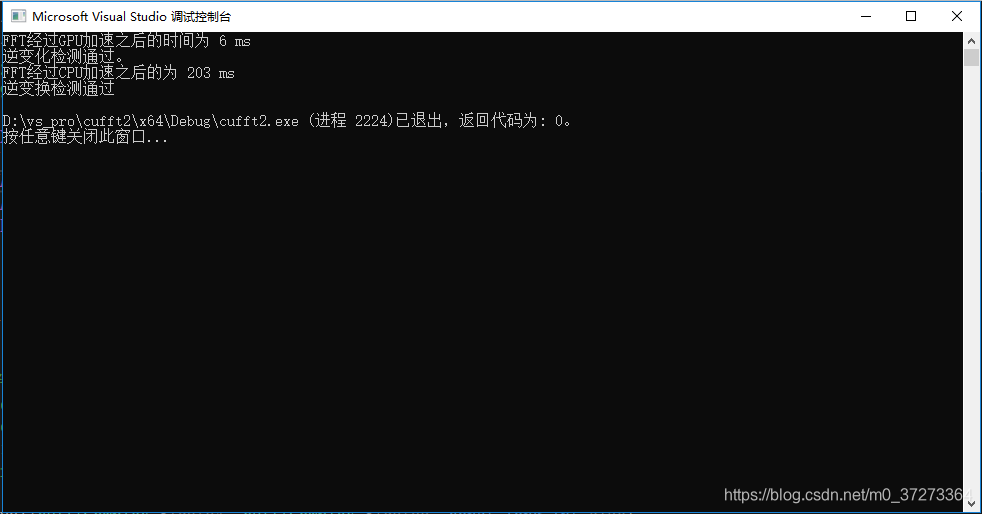
2^18

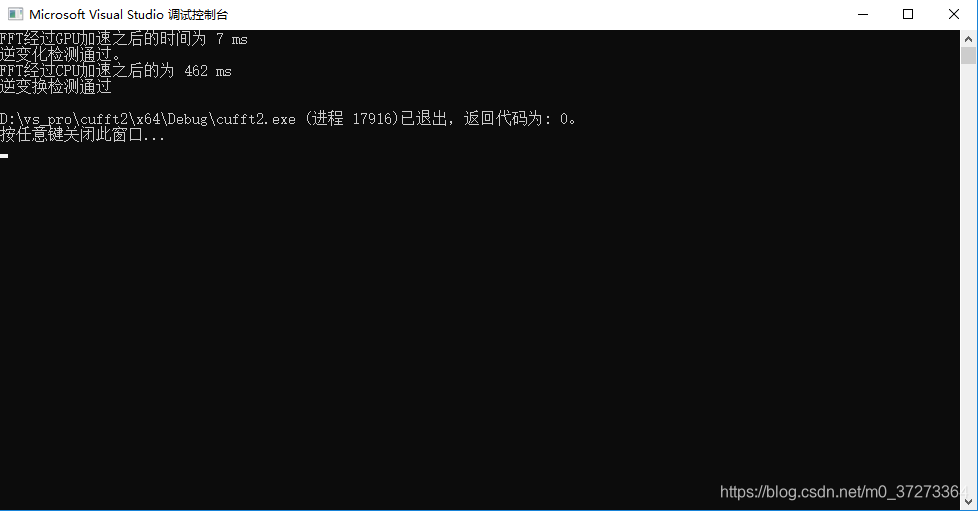
六、實驗結果分析

根據執行的時間對比，可以看出，隨著資料集的增加，CPU的處理時間和資料集的增加速率基本同步（資料集增大兩倍，CPU處理時間增大兩倍），而GPU的處理時間基本不變。

之前在做小資料集的時候發現經過GPU的加速執行時間和CPU的執行時間不相上下，甚至比CPU還要慢。

通過分析可以知道，當資料集較小時，資料在相關暫存器/記憶體的傳送的時間對總時間的貢獻更大主要，而當資料集很大的時候，計算時間對總時間的貢獻更大。為了比較效能，於是就沒有放小資料集的執行情況。

可以看到，對於大資料集，經過GPU加速，計算時間基本維持在了一個常數時間（其中也有程式執行的偶然性以及計時精度的問題，實際上執行時間應該線性增加，但是速率比CPU的2倍速慢）

七、思考題

分析GPU加速FFT程式可能獲得的加速比

理論上，如果GPU可以一次儲存完所有的資料，那麼相對於CPU，資料傳送的時間可以忽略，而CPU能夠一次處理的資料塊的大小有限，理論的加速比應該是GPU一次可以處理的資料塊大小/CPU一次可以處理的資料塊大小，因為實際上GPU就是對多個數據塊的並行運算。但是這個加速比不可知（需要查閱相關的資料手冊，但是我沒有找到）

實際加速比相對於理想加速比差多少？原因是什麼？

原因：

每次執行程式時，資料在CPU/GPU和記憶體之間的傳送時間不同（依賴於當時計算機的執行情況）

GPU上進行的類多執行緒方式的時間開銷以及寫回/驗證時的可能存在的寫衝突