動態時間規整演算法(Dynamic Time Warping, DTW)之初探單詞語音識別
動態時間規整演算法(DTW)是最近接觸的一種提取時間序列模板方法。本文主要是一些自己的學習記錄,並適當地加入自己的理解。若有見解不一致之處,歡迎交流。
1 動態時間規整(DTW)基本思想
先從單詞語音時間序列的規整問題引入DTW的基本思想。
假設下圖兩個時間序列對應的是同一個單詞的發音(實則不是,只是為了便於理解)。黑色的線表示兩個時間序列的相似的點(用幅度差異刻畫時間序列點的相似性,幅度差異越小,相似性越高)。由於不同人語速上存在差異,某些人可能會把字母‘A’發得很長(延長髮音),某些人卻發得較短(短促發音),這樣同一個字母展現出來的時間序列上就存在著很大的差異,如圖中綠色圈出的時間波形所示。因此就需要對原始的兩個時間序列進行規整,即對時間序列進行延伸和縮短,提取兩個時間序列的相似性,從而對語音進行識別。
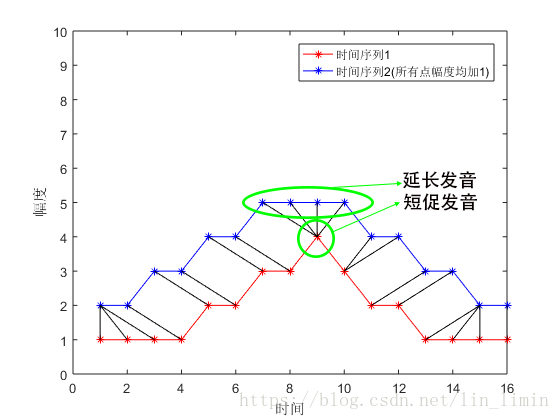
圖1 動態時間規整基本思想
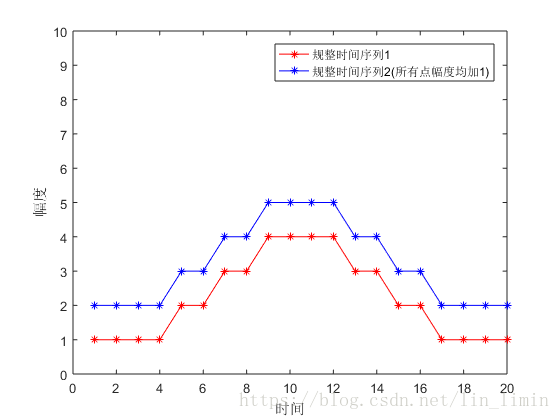
圖2 時間序列規整結果
圖2對應的就是原始時間序列的規整結果。
所以動態時間規整的思想就是:通過對兩個時間序列點之間的相似性進行比較(圖1黑線),對原始時間序列進行拉伸到相同時間長度(原始時間序列的長度很可能不一致),進而比較兩個時間序列的相似性。
動態時間規整要解決的問題就是:找到一條最優的規整路徑,其中,即認為時間序列1的第i個點和時間序列2的第j個點是相似的。所有相似點的距離之和作為規整路徑距離,用規整路徑距離來衡量兩個時間序列的相似性。規整路徑距離越小,相似度越高。
2 動態規劃解DTW問題
假設原始時間序列為X,Y,它們的時間長度分別為和。對於規整路徑,有:
k表示兩個序列最終被拉伸的長度。
規整路徑必須從開始,到結束,以保證X和Y序列的每個座標點都出現一次。另外,規整路徑中的i和j必須是單調遞增的,所謂單調遞增指的是:
所以如果路徑已經通過了格點(i,j),那麼路徑的下一個格點只能是(i+1,j),(i,j+1),(i+1,j+1)中的一種,如圖3中綠色剪頭所示。
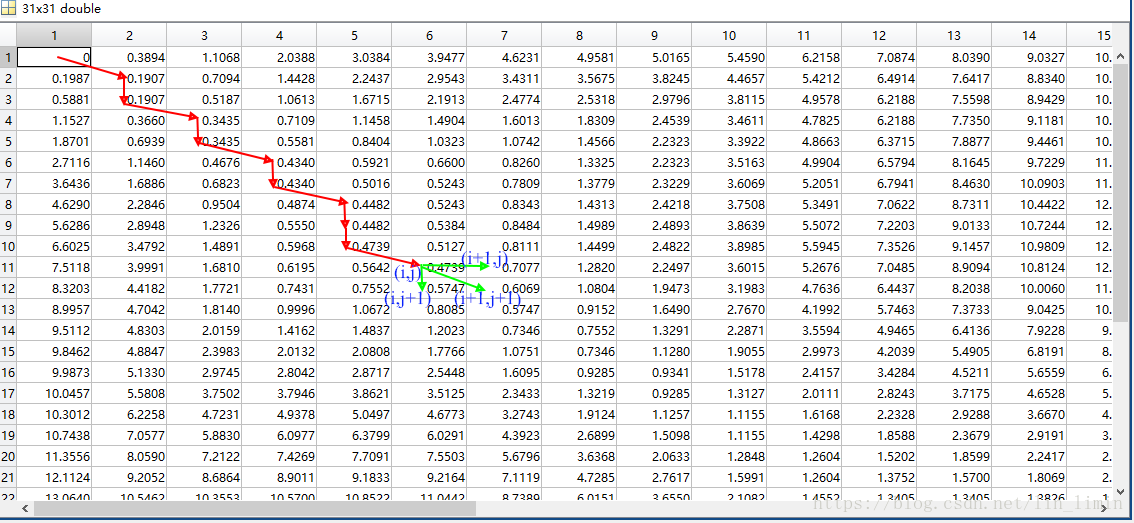
圖3 規整路徑示意
所以對於路徑規整距離矩陣,有:
其中,表示X序列第i個點與Y序列第j個點之間的距離(兩個點的相似性)。衡量的是X序列前i個點與Y序列前j個點的相似性。最終的規整路徑距離為。的值越小,兩個原始時間序列的相似性越大。
有了式子(3),我們就可以用動態規劃來對DTW問題進行求解。
設定不一樣的取樣頻率對正弦函式進行取樣,得到兩個原始時間序列如圖4所示。其中時間序列1的前半段取樣頻率低於時間序列2前半段的取樣頻率,後半段高於時間序列2的取樣頻率。利用動態規劃的遞推公式(3)可以求得路徑規整矩陣如圖5所示。由可得規整路徑如圖6所示。規整路徑規定了時間序列X與時間序列Y的時間對齊方式。由此可以得到如圖7所示的規整時間序列。可見,在DTW的作用下,完成了兩個時間序列的規整目標。
這邊程式碼借鑑於動態時間規整借鑑程式碼,在此多謝博主!!
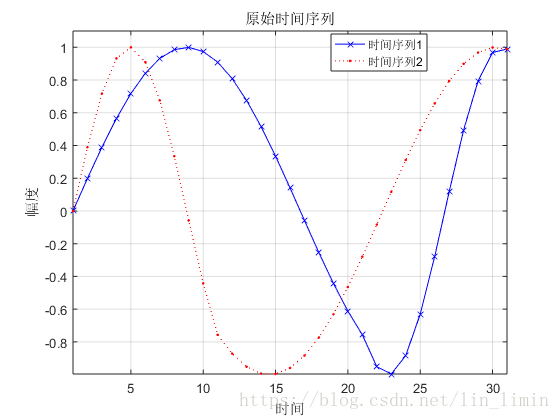
圖4 取樣頻率不同而生成的兩個原始時間序列
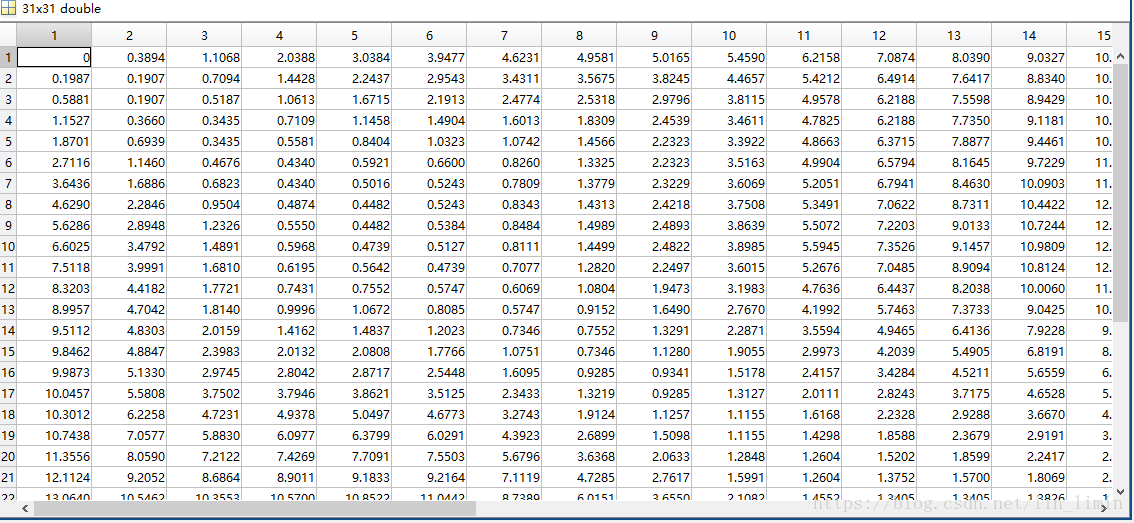
圖5 規整距離矩陣
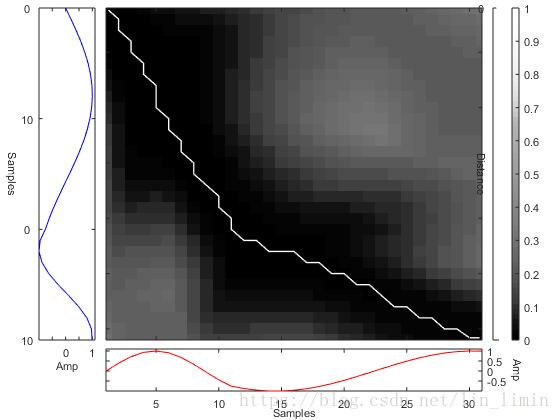
圖6 規整路徑
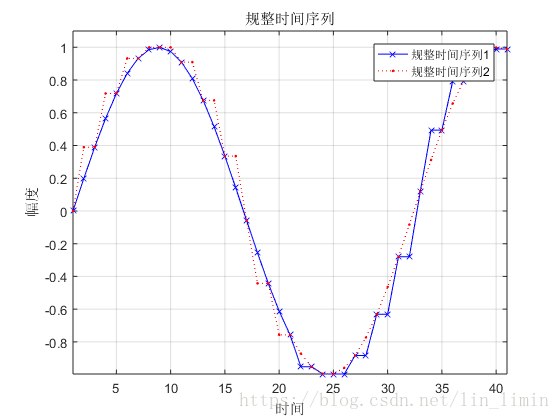
圖7 DTW規整後的時間序列
圖7所示的規整序列基本達到了時間序列的對齊目的。可是,如果有兩個時間序列的幅值不同,將會產生什麼樣的規整結果?圖9是對圖8進行規整得到的規整時間序列。由此可知,最終的效果並不理想。為了使得DTW能夠提取原始序列的時間特徵而忽略幅值對序列規整的影響,我在原有程式碼的基礎上加入了zscore對原始資料進行標準化。最終的結果如圖10所示。
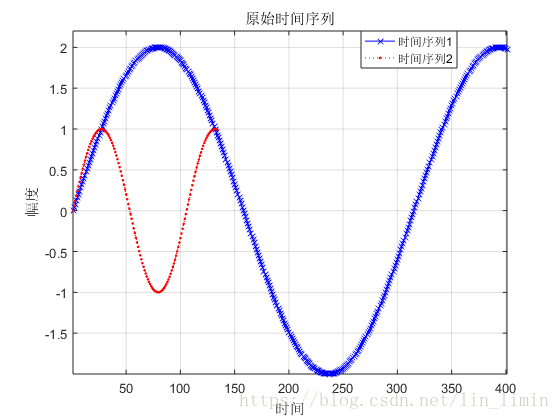
圖8 具有不同幅值的兩個原始時間序列
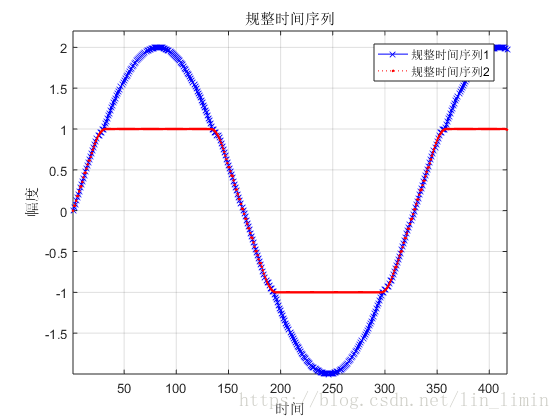
圖9 不同幅值時間序列的規整結果
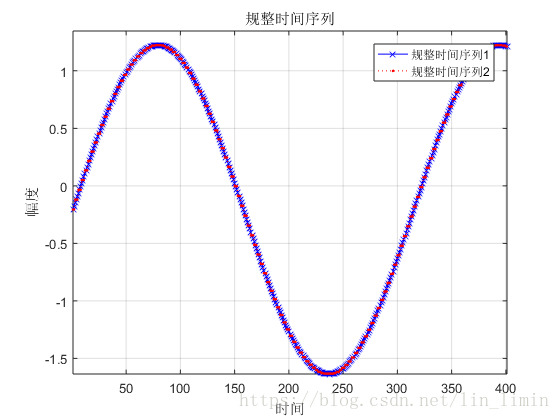
圖10 加入zscore標準化處理後的規整結果
3 一個簡單的單詞語音音訊識別例項
●語音時間序列規整
這邊我利用自己錄製的幾段單詞mp3檔案來探討動態時間規整演算法對語音時間序列的對齊。圖11所示為兩段‘water’這個單詞的語音時間序列。由於語速和發音時刻的差異,兩個原始序列之間存在差異,但明顯可以看出兩者之間有很大的相似性。利用第2小節闡述的DTW演算法,最終的語音規整結果如圖12所示,基本達到了目的。當然這邊做的非常粗糙,比如語音裡面的很多毛刺,低頻訊號完全可以用濾波的方式先消掉,然後再交由DTW進行處理。
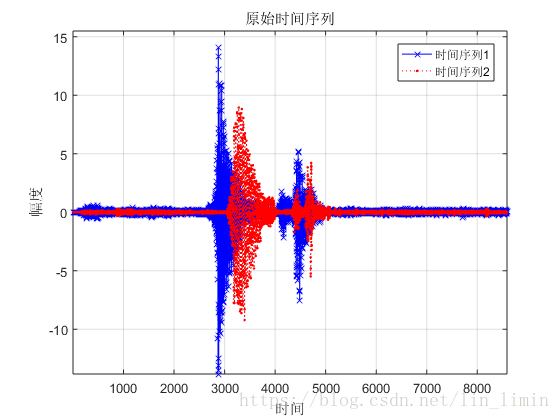
圖11 兩段’water’音訊的原始時間序列
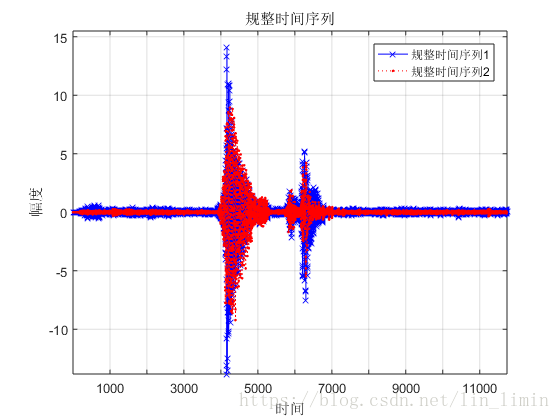
圖12 語音時間序列規整
●單詞語音音訊識別
如何利用DTW演算法來做簡單的語音音訊識別?第2小節已經提及,DTW做序列規整時利用規整路徑距離來衡量時間序列X和時間序列Y的相似性。所以,假設我們現有‘water’,’teacher’,’apple’的幾段音訊序列,要識別某一個音訊的發音到底是這三個單詞中的哪一個,就只需要將這個待識別音訊序列分別與三個單詞的音訊序列做規整,得到各自的規整路徑距離(即附錄程式碼中的變數Dist)。越小,說明兩者的相似度越高。這樣可以初步完成單詞語音音訊識別的任務。當然,實際上進行這樣操作的複雜度是很高的,實用性很差。
4 總結
① 動態時間規整演算法(DTW)是一種時間序列對齊方法。它通過尋找一條規整路徑來使得規整距離最小。規整路徑距離表徵了兩個時間序列的相似性:越小,相似度越高。
② 可以利用DTW演算法來做單詞音訊的識別。
