參考網址：http://iamtrask.github.io/2015/07/12/basic-python-network/ 先上程式碼

X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
syn0 = 2*np.random.random((3,4)) - 1       #隨機初始化權重
syn1 = 2*np.random.random((4,1)) - 1       #隨機初始化權重
for j in xrange(60000):                    #迭代次數
    l1 = 1/(1+np.exp(-(np.dot(X,syn0))))    #正向傳播
    l2 = 1/(1+np.exp(-(np.dot(l1,syn1))))   #正向傳播
    l2_delta = (y - l2)*(l2*(1-l2))         #反向傳播
    l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))   #反向傳播
    syn1 += l1.T.dot(l2_delta)              #更新權重
    syn0 += X.T.dot(l1_delta)               #更新權重
 

看起來是不是很簡單呢，這11行程式碼就構建了一個3層的神經網路（一個輸入、一個輸出、一個隱層），下面兩張圖可能幫你理解上面程式碼中的公式含義                          左圖：神經網路形式（單一樣本）                                             右圖：反向傳播公式 如果沒看懂，沒關係，作者進行了分佈講解： 訓練反向傳播神經網路的目的是為了根據輸入預測輸出結果 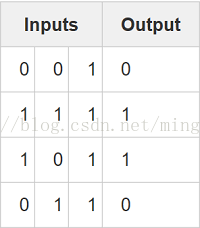考慮使用給定三個輸入資料預測輸出資料， 我們可以通過簡單地測量輸入值和輸出值之間的統計資訊來解決這個問題。 如果我們這樣做，我們將看到最左邊的輸入列與輸出完全相關。

這就是反向傳播最簡單的作用形式，下面讓我們開始求解吧。 （1）2層網路

import numpy as np

# sigmoid 函式，也可以求導用
def nonlin(x,deriv=False):
    if(deriv==True):
        return nonlin(x)*(1-nonlin(x))
    return 1/(1+np.exp(-x))
    
# input dataset
X = np.array([  [0,0,1],
                [0,1,1],
                [1,0,1],
                [1,1,1] ])
    
# output dataset            
y = np.array([[0,0,1,1]]).T

# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)

# 隨機初始化均值為0的權重，目的是打破對稱性，否則更新權重值可能相同
syn0 = 2*np.random.random((3,1)) - 1

for iter in xrange(10000):

    # forward propagation
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))

    # how much did we miss?
    l1_error = y - l1

    # multiply how much we missed by the 
    # slope of the sigmoid at the values in l1 反向傳播公式
    l1_delta = l1_error * nonlin(l1,True)

    # update weights
    syn0 += np.dot(l0.T,l1_delta)

print "Output After Training:"
print l1
 

Output After Training:
[[ 0.00966449]
 [ 0.00786506]
 [ 0.99358898]
 [ 0.99211957]]

變數含義： 結果表明神經網路工作了，最好可以自己程式設計嘗試一下，有幾點值得關注： （1）迭代前後l1的變化 （2）觀察nonlin函式，它給出了概率預測 （3）迭代過程中l1_error的變化（是否在逐漸變小呢） （4）BP的大部分祕密都在下面這行程式碼中

l1_delta = l1_error * nonlin(l1,True)

（5）所做的一切努力都是為了下面這行程式碼

syn0 += np.dot(l0.T, l1_delta)

程式碼逐行解析：

（1）第一行載入numpy函式庫

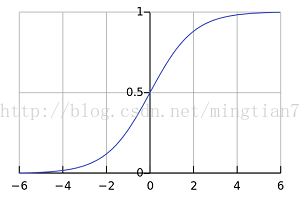
（2）第四行定義sigmoid函式，取值[0,1]，用它來表示概率

（3）第五行定義sigmoid導數，如果deriv == True，那麼返回out*(1-out) ,out = sigmoid(z)

（4）第十行使用numpy中的矩陣初始化資料，每一行代表一個數據，每一列對應著神經網輸入節點，本例中有4個數據，3個輸入節點

（5）第十六行初始化輸出資料，T代表轉置，y具有4行1列，與輸入資料相對應。因此對於每個樣本，有3個輸入，1個輸出。

（6）第二十行隨機初始化權重，每次訓練後仍會隨機分佈，更利於觀察神經網路的變化（打破對稱性）。

（7）第二十三行syn0為連線權重，因為只有輸入層和輸出層，因此只需要一個權重矩陣。其尺寸為3*1是因為我們有3個輸入，一個輸出。syn0代表了這個神經網路的全部引數，神經網路的效能與輸入資料和輸出資料無關。

（8）第二十五行開始訓練網路，設定訓練次數

（9）第二十八行初始層l0就是我們的輸入資料，我們有4個數據，更新神經網路將會全部使用（而不是使用某幾個），這稱為"full batch"。

（10）第二十九行正向傳播過程，也就是預測過程。首先是根據連線權重計算輸出（l0*sy0），（4*3）dot （3*1）= （4*1）。再對四個樣本計算出的結果使用sigmoid函式預測其為1的概率。

（11）第三十二行計算每個結果的預測結果和實際結果相差多少，就是誤差

（12）第三十六行就是反向傳播公式了，用來更新權重係數（最重要的），分a,b部分進行講解

a.首先看看nonlin(l1,True),它代表sigmoid函式的梯度：

可以看到當x->0時，數值較大，越偏離0，這個數值越小

b.再來看這行程式碼

 l1_delta = l1_error * nonlin(l1, True)

l1_error是4*1，nonlin(l1,True)是4*1，*為對應元素相乘，l1_delta仍為4*1。它這種做法的含義在於減小高可信樣本的預測誤差。什麼意思呢？當某一樣本預測結果l1接近1或者0時都代表著神經網路高度肯定這是個正例或者反例，即再下次更新時該樣本的誤差權重應該低一些（對更新weight係數作用較小），其表現在nonlin（l1,True）返回的值較低，若l1接近0.5，即判斷正例的概率為0.5，完全不確定嘛，應該加大下次更新時其誤差權重（對更新weight係數作用較大），表現在nonlin(l1,True)返回值較大。

（13）第三十九行更新神經網路，首先看單一樣本

更新公式：

weight_update = input_value * l1_delta

從左到右進行更新，第一個元素就是1*l1_delta，這個更新值不會使得新的SYN0(1)偏離9.5太遠，為什麼呢？因為預測值為0.99，說明神經網路充分自信，此時顯然l1_error、nonlin(l1,True)都比較小，因此不會怎麼改變原始權重係數。由於更新時會使用所有樣本，過程為求和取平均，因此實際的更新過程如下：

 因此，簡單點說，反向神經網路更新過程就是根據樣本預測的正確性，不斷調整樣本誤差的權重，即更新weights時不同樣本的作用權重不同，直至網路儘量擬合所有樣本。

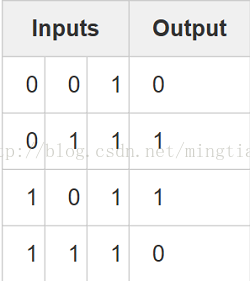（2）複雜一點的問題（3層網路） 網路如果只有輸入層和輸出層的話（2層）之沒有辦法解決非線性問題的，例如非常簡單異或問題： 因此要引入多層神經網路（包含隱層），例如本文開頭的那段小程式對應的網路結構啦。 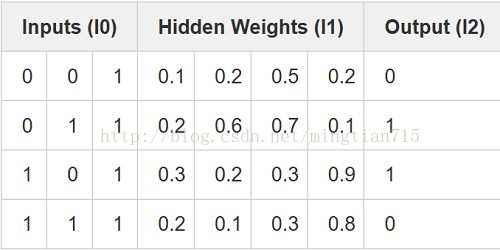正向傳播的過程就是輸入4*3的資料，乘上第一層的權重矩陣3*4，得到隱層矩陣l1(4*3)dot(3*4) = (4*4)，如上圖所示，再乘第二層權重矩陣(4*1)，得到輸出l2(4*4)dot(4*1) = （4*1），當然都沒考慮sigmoid函式，只是表明這個過程。 對於反向傳播過程，如果你已經理解了兩層網路的權重更新過程，三層也是相似，每一層權重更新都和其更深一層的誤差息息相關。 程式碼：

import numpy as np

def nonlin(x,deriv=False):
	if(deriv==True):
	    return x*(1-x)

	return 1/(1+np.exp(-x))
    
X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])
                
y = np.array([[0],
			[1],
			[1],
			[0]])

np.random.seed(1)

# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1

for j in xrange(60000):

	# Feed forward through layers 0, 1, and 2
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))
    l2 = nonlin(np.dot(l1,syn1))

    # how much did we miss the target value?
    l2_error = y - l2
    
    if (j% 10000) == 0:
        print "Error:" + str(np.mean(np.abs(l2_error)))
        
    # in what direction is the target value?
    # were we really sure? if so, don't change too much.
    l2_delta = l2_error*nonlin(l2,deriv=True)

    # how much did each l1 value contribute to the l2 error (according to the weights)?
    l1_error = l2_delta.dot(syn1.T)
    
    # in what direction is the target l1?
    # were we really sure? if so, don't change too much.
    l1_delta = l1_error * nonlin(l1,deriv=True)

    syn1 += l1.T.dot(l2_delta)
    syn0 += l0.T.dot(l1_delta)

Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786

翻譯中包含了一些自己的理解~ 因此如果有問題的話，敬請指正！