Imp is watching a documentary about cave painting.

Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.

Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all 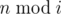, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:

• 1 ≤ i < j ≤ k,
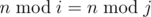• , where  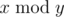is the remainder of division x by y.

The only line contains two integers n, k (1 ≤ n, k ≤ 1018).

Print "Yes

You can print each letter in arbitrary case (lower or upper).

4 4

No

5 3

Yes

In the first sample remainders modulo 1 and 4 coincide.

題意：輸入n，k，求所有1<=i<j<=k,是否滿足n%i！=n%j，若滿足 輸出Yes，否則 輸出No，也就是n%（1~k）所有的數取餘，餘數是不是都不一樣；

這個道題的突破點是，所有數對1取餘都等於0,假如 一個數n mod 1 = 0，n mod 2 只能等於0或1，因0被佔了，只能是1，n mod 3 因0,1被佔了只能是2，依次類推，只要判斷 n%i == i-1 即可，因為n和k的範圍，剛開始暴力，你心裡一定沒有底，在這裡我們構造一個 1~k Yes的最小n，看n的範圍，為什麼這麼構造呢，因為滿足 (1<=i<=k) n%i == i-1 k的範圍一定不是太大；構造一個1~k Yes的最小n，實際上是lcm(1<=i<=k) - 1;首先說一下為什麼,lcm(1<=i<=k) 對 1~k中所有的數取餘一定是 0，所以 ( lcm(i<=i<=k) - 1 )% i  = i - 1,也就是 i 的公倍數 - 1 對 i 取餘，這一定等於 i-1 啊；不懂得自己舉個例子，下面給出一幅圖，左邊是k，右邊是Yes的最小n

程式碼：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int main()
{
	__int64 i,j,k,n;
	while(~scanf("%I64d%I64d",&n,&k))
	{
		int f = 0;	
		for(i = 1;i<=k;i++)
		{
			if(n%i!=i-1)
			{
				f = 1;
				break;
			}
		}
		if(f) printf("No\n");
		else printf("Yes\n");		
	}
	return 0;
}