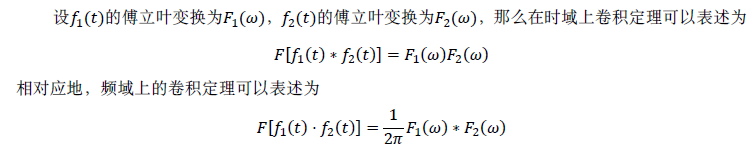http://blog.csdn.net/baimafujinji/article/details/48467225

1.4.5   卷積定理及其證明

卷積定理是傅立葉變換滿足的一個重要性質。卷積定理指出，函式卷積的傅立葉變換是函式傅立葉變換的乘積。換言之，一個域中的卷積對應於另一個域中的乘積，例如，時域中的卷積對應於頻域中的乘積。

這一定理對拉普拉斯變換、Z變換等各種傅立葉變換的變體同樣成立。需要注意的是，以上寫法只對特定形式的變換正確，因為變換可能由其它方式正規化，從而使得上面的關係式中出現其它的常數因子。
下面我們來證明時域卷積定理，頻域卷積定理的證明與此類似，讀者可以自行證明。
證明：將卷積的定義

傅立葉變換的作用在頻域對訊號進行分析，我們可以把時域的訊號看做是若干正弦波的線性疊加，傅立葉變換的作用正是求得這些訊號的幅值和相位。既然固定的時域訊號是若干固定正弦訊號的疊加，在不改變幅值的情況下，在時間軸上移動訊號，也就相當於同時移動若干正弦訊號，這些正弦訊號的相位改變、但幅值不變，反映在頻域上就是傅立葉變換結果的模不變、而相位改變。所以，時移性質其實就表明當一個訊號沿時間軸平移後，各頻率成份的大小不發生改變，但相位發生變化。
既然這裡提到了傅立葉變換的性質，這裡我們還將補充一些關於帕塞瓦爾定理的有關內容。該定理最早是由法國數學家帕塞瓦爾（Marc-Antoine Parseval）在1799年推匯出的一個關於級數的理論，該定理隨後被應用於傅立葉級數。帕塞瓦爾定理的表述是這樣的：

綜上所述，原結論得證。
前面我們也介紹過複數形式的傅立葉級數，下面我們來推導與複數形式傅立葉變換相對應的帕塞瓦爾等式。這裡再次給出傅立葉級數的複數形式表示式，具體推導過程請讀者參閱前文

帕塞瓦爾定理把一個訊號的能量或功率的計算和頻譜函式或頻譜聯絡起來了，它表明一個訊號所含有的能量（功率）恆等於此訊號在完備正交函式集中各分量能量（功率）之和。換言之，能量訊號的總能量等於各個頻率分量單獨貢獻出來的能量的連續和；而週期性功率訊號的平均功率等於各個頻率分量單獨貢獻出來的功率之和。

我的“影象處理中的數學原理”專欄中之系列文章已經以《影象處理中的數學修煉》為名結集出版（清華大學出版社）。該書詳細介紹影象處理中的數學原理，為你開啟一道通往影象世界的數學之門，詳細內容及目錄請見 http://blog.csdn.net/baimafujinji/article/details/48467225