2018年全國多校演算法寒假訓練營練習比賽(第一場)
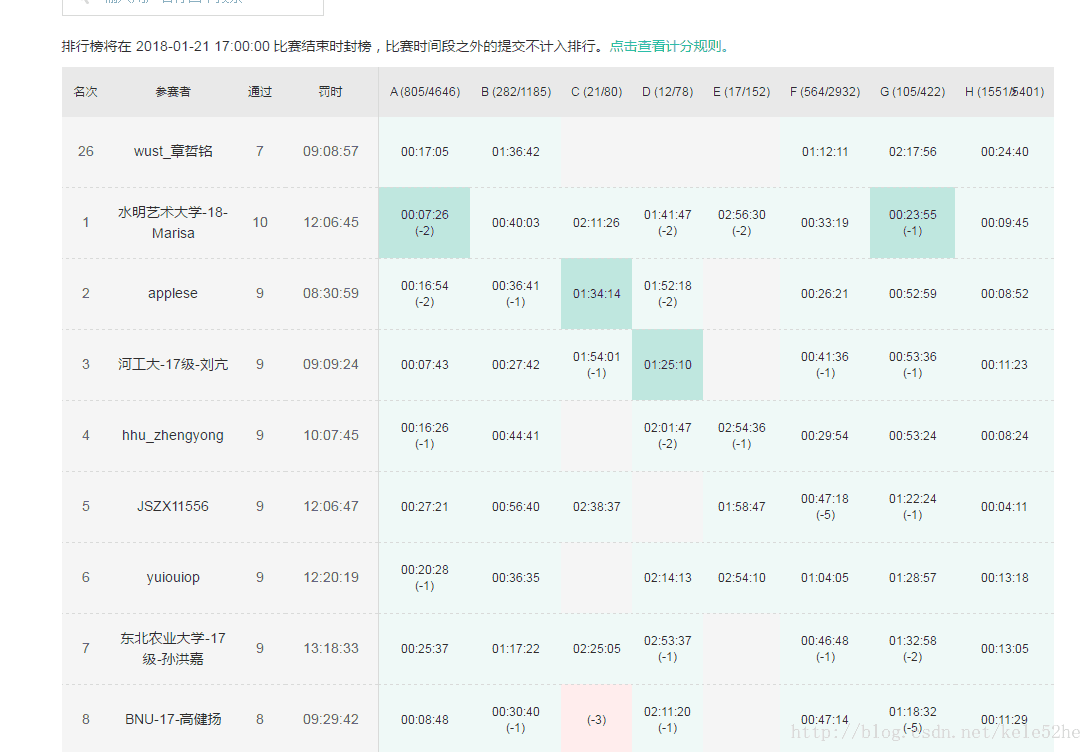
這是一場拼手速和細節的比賽,難題並不多,我做的七道題裡沒有一道涉及演算法。我雖然做的有點慢,但是七道題全部1A,其中J題的規律想半天想不出來,感謝Winzard大神出手相助告訴了我hhhhh,最後拿了第26名,還算可以吧。
首先把n把槍的屬性全部記錄下來,然後對m個配件進行處理,處理出每一類配件的最高屬性值,代回n把槍中,再對n把槍遍歷一遍,就處理出了威力最高的槍,也就是答案。
B題:最強的決鬥者一切都是必然的!#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <cstdlib> #include <cmath> #include <vector> #include <queue> #include <iterator> #include <map> #include <algorithm> #include <set> #include <functional> #include <time.h> #define lson rt<<1 #define rson rt<<1|1 using namespace std; typedef long long LL; typedef unsigned long long ULL; const int INF = 1e9 + 5; const int MAXN = 100005; const LL MOD = 1000000007; const double eps = 1e-8; const double PI = acos(-1.0); LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); } LL ppow(LL a, LL b) { LL res = 1; for (int i = 1; i <= b; i++) res *= a; return res; } LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; } struct gun { double power; int num; int add[1005]; }; gun G[1005]; double add[1005]; int main() { double res,ans,b; int q; int n, m; while (scanf("%d%d", &n, &m) != EOF) { ans = 0; memset(add, 0, sizeof add); for (int i = 1; i <= n; i++) { scanf("%lf", &G[i].power); scanf("%d", &G[i].num); for (int j = 1; j <= G[i].num; j++) scanf("%d", &G[i].add[j]); } for (int i = 1; i <= m; i++) { scanf("%d%lf", &q, &b); if (add[q] - b < -eps) add[q] = b; } for (int i = 1; i <= n; i++) { res = 1; for (int j = 1; j <= G[i].num; j++) res += add[G[i].add[j]]; res *= G[i].power; if (res - ans > eps) ans = res; } printf("%.4lf\n", ans); } }
首先按順序處理出每一次連鎖的範圍,對於樣例來說,一共有三次連鎖,分別是1~4,5~6,7~9。對於每一次連鎖,我們從後往前迴圈分析,因為後連鎖的先發動,如果是type1就直接ans+=x,如果是type2就ans+=x*p,如果是type3我們就可以直接跳出該連鎖,處理下一個連鎖,如果是type4我們就跳過一張卡。最後處理完所有連鎖後,ans就是總傷害。
F題:大吉大利,今晚吃雞——跑毒篇#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <cstdlib> #include <cmath> #include <vector> #include <queue> #include <iterator> #include <map> #include <algorithm> #include <set> #include <functional> #include <time.h> #define lson rt<<1 #define rson rt<<1|1 using namespace std; typedef long long LL; typedef unsigned long long ULL; const int INF = 1e9 + 5; const int MAXN = 100005; const LL MOD = 1000000007; const double eps = 1e-8; const double PI = acos(-1.0); LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); } LL ppow(LL a, LL b) { LL res = 1; for (int i = 1; i <= b; i++) res *= a; return res; } LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; } struct card { int speed; int type; int x; }; LL ans; card C[1005]; int l, r; void solve() { for (int i = r; i >= l; i--) if (C[i].type == 1) ans += C[i].x; else if (C[i].type == 2) ans += C[i].x*(i - l + 1); else if (C[i].type == 3) return; else if (C[i].type == 4) i--; } int main() { int n, p; while (scanf("%d", &n) != EOF) { ans = 0; l = 1; r = 1; for (int i = 1; i <= n; i++) { scanf("%d%d", &C[i].speed, &C[i].type); if (C[i].type == 1 || C[i].type == 2) scanf("%d", &C[i].x); } while (l <= n&&r <= n) { p = C[l].speed; while (r + 1 <= n&&C[r + 1].speed >= p) p = C[++r].speed; solve(); l = r + 1; r = l; } printf("%lld\n", ans); } }
這道題資料範圍很小,我們直接用最暴力的模擬即可,也就是每一秒每一秒的模擬,每一秒都判斷一下下一回合不用急救包會不會死,如果會死就用急救包,否則就前進,如果要用急救包的時候再判斷一下當前狀態不用急救包能否走到終點和急救包是否夠用,反正就是題目是什麼要求我們就怎麼寫。
G題:圓圈#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <cstdlib> #include <cmath> #include <vector> #include <queue> #include <iterator> #include <map> #include <algorithm> #include <set> #include <functional> #include <time.h> #define lson rt<<1 #define rson rt<<1|1 using namespace std; typedef long long LL; typedef unsigned long long ULL; const int INF = 1e9 + 5; const int MAXN = 100005; const LL MOD = 1000000007; const double eps = 1e-8; const double PI = acos(-1.0); LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); } LL ppow(LL a, LL b) { LL res = 1; for (int i = 1; i <= b; i++) res *= a; return res; } LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; } int a, b, c; int hp; bool solve() { hp = 100; for (int t = 1; t <= b; t++) { hp -= a; if (hp - a * 7 <= 0) if (hp - a*(b - t - 1) > 0) return true; else if (c > 0 && a * 6 < 100) { hp = 80; c--; } else return false; } return true; } int main() { bool ans; int T; scanf("%d", &T); while (T--) { scanf("%d%d%d", &a, &b, &c); ans = solve(); if (ans) printf("YES\n"); else printf("NO\n"); } }
一道標準的遞迴圖形輸出問題,這類問題有通解:遞迴圖形輸出問題通解
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <iterator>
#include <map>
#include <algorithm>
#include <set>
#include <functional>
#include <time.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int INF = 1e9 + 5;
const int MAXN = 100005;
const LL MOD = 1000000007;
const double eps = 1e-8;
const double PI = acos(-1.0);
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }
LL ppow(LL a, LL b) { LL res = 1; for (int i = 1; i <= b; i++) res *= a; return res; }
LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; }
bool a[3000][3000];
void draw(int x, int y, int n)
{
int temp = ppow(3, n - 1);
if (n == 0) {
a[x][y] = true;
}
else {
draw(x - temp, y, n - 1);
draw(x + temp, y, n - 1);
draw(x, y - temp, n - 1);
draw(x, y + temp, n - 1);
}
}
int main()
{
int T,n,x;
int len;
bool space;
scanf("%d", &T);
while (T--)
{
memset(a, 0, sizeof a);
scanf("%d", &n);
len = ppow(3, n);
x = (len + 1) / 2;
draw(x, x, n);
for (int i = 1; i <= len; i++)
{
space = true;
for (int j = 1; j <= len; j++)
if (a[i][j])
{
printf("O");
space = false;
for (int t = j + 1; t <= len; t++)
if (a[i][t])
space = true;
}
else
if (space)
printf(" ");
else
break;
printf("\n");
}
}
}斐波那契數列
I題:找數字個數
資料範圍很小,把他給你的數字進行數位處理,不能選的數打上標記,然後直接1到1000的迴圈,答案就出來了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <iterator>
#include <map>
#include <algorithm>
#include <set>
#include <functional>
#include <time.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int INF = 1e9 + 5;
const int MAXN = 100005;
const LL MOD = 1000000007;
const double eps = 1e-8;
const double PI = acos(-1.0);
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }
LL ppow(LL a, LL b) { LL res = 1; for (int i = 1; i <= b; i++) res *= a; return res; }
LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; }
bool numok[10];
int a, b;
void solve(int x)
{
int res;
while (x)
{
res = x % 10;
x /= 10;
numok[res] = false;
}
}
bool check(int x)
{
if (x%a == 0 || x%b == 0)
return false;
int res;
while (x)
{
res = x % 10;
x /= 10;
if (numok[res] == false)
return false;
}
return true;
}
int main()
{
int T;
int ans;
scanf("%d", &T);
while (T--)
{
ans = 0;
for (int i = 0; i < 10; i++)
numok[i] = true;
scanf("%d%d", &a, &b);
solve(a);
solve(b);
for (int i = 1; i <= 1000; i++)
if (check(i))
ans++;
printf("%d\n", ans);
}
}這題題目裡沒告訴你規律,要自己找,找到了就很簡單。奇數層會給你一個0,偶數層會給你一個1和一個0。
2個0->1個1,3個1->1個2,4個2->1個3,5個3->1個4,以此類推。
那麼第n層一共會給你n個0和n/2個1,我們用一個數組記錄這些數字的個數,比如說num[p]就是指p的個數,那我們就可以得到一個遞推操作,num[p]=num[p-1]/(p+1),num[p-1]%=(p+1),這就是把p-1轉化成p的操作。我們從p=1開始執行這個操作,直到num[p-1]/(p+1)=0為止,即無法繼續轉化成更大的數了。然後我們從p到0迴圈一遍,對於每一個i輸出num[i]次就是答案。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <iterator>
#include <map>
#include <algorithm>
#include <set>
#include <functional>
#include <time.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int INF = 1e9 + 5;
const int MAXN = 100005;
const LL MOD = 1000000007;
const double eps = 1e-8;
const double PI = acos(-1.0);
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }
LL ppow(LL a, LL b) { LL res = 1; for (int i = 1; i <= b; i++) res *= a; return res; }
LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; }
int num[1005];
int main()
{
int T, n, p;
scanf("%d", &T);
while (T--)
{
memset(num, 0, sizeof num);
scanf("%d", &n);
num[0] = n;
num[1] = n / 2;
p = 1;
while (num[p - 1] / (p + 1)>0)
{
num[p] += num[p - 1] / (p + 1);
num[p - 1] %= (p + 1);
p++;
}
for (int i = p - 1; i >= 0; i--)
for (int j = 0; j < num[i]; j++)
printf("%d", i);
printf("\n");
}
}