這裡接著學習筆記一中的問題2，說實話問題2中的Baum-Welch演算法程式設計時矩陣轉換有點燒腦，開始編寫一直不對（程式設計還不熟練hh），後面在紙上仔細推了一遍，由特例慢慢改寫才執行成功，所以程式碼裡面好多處都有print。

　　筆記一中對於問題1（概率計算問題）採用了前向或後向演算法，根據前向和後向演算法可以得到一些後面要用到的概率與期望值。

一、問題2 學習問題  已知觀測序列，估計模型引數，使得在該模型下觀測序列概率最大

　　隱馬爾可夫模型的學習，根據訓練資料除包括觀測序列O外是否包括了對應的狀態序列 I 分為監督學習和非監督學習。如果包括了狀態序列 I ，則可以直接採用極大似然估計來估計隱馬爾可夫模型的初始狀態概率Pi，狀態轉移概率A和觀測概率B（一般統計頻數）。但是一般沒有對應的狀態序列 I ，如果人工標註訓練資料的話代價太高，所以大多時候採用非監督學習方法------Baum-Welch演算法。

　　Baum-Welch演算法

　　假設給定訓練資料只包含S個長度為T的觀測序列而沒有對應的狀態序列，目標是學習隱馬爾可夫模型的引數。我們將觀測序列資料看作觀測資料O，狀態序列資料看作不可觀測的隱資料I，那麼隱馬爾可夫模型事實上是一個含有隱變數的概率模型

它的引數學習可以由EM演算法實現（EM演算法可以參考部落格，博主寫得通俗易懂）。

　　1、確定完全資料的對數似然函式

　　所有觀測資料寫成,所有隱資料寫成，完全資料是。完全資料的對數似然函式是。

　　2、EM演算法的E步：

　　求Q函式

其中，是隱馬爾可夫模型引數的當前估計值，是要極大化的隱馬爾可夫模型引數。（Q函式的標準定義是：

於是函式可以寫成：

式中求和都是對所有訓練資料的序列總長度T進行的。這個式子是將代入後（取對數後變成加法，便於求解），將初始概率、轉移概率、觀測概率這三部分乘積的對數拆分為對數之和，所以有三項。

　　3、EM演算法的M步:極大化Q函式求模型引數，由於要極大化的引數在Q函式表示式中單獨地出現在3個項中，所以只需對各項分別極大化。

　　第1項可以寫成：

注意到滿足約束條件利用拉格朗日乘子法，寫出拉格朗日函式：

對其求偏導數並令結果為0

得到

這個求導是很簡單的，求和項中非i的項對πi求導都是0，logπ的導數是1/π，γ那邊求導就剩下πi自己對自己求導，也就是γ。等式兩邊同時乘以πi就得到了上式。

對i求和得到γ：

代入中得到：

第2項可以寫成：

類似第1項，應用具有約束條件的拉格朗日乘子法可以求出

第3項為:

同樣用拉格朗日乘子法，約束條件是。注意，只有在對時對的偏導數才不為0,以表示。求得

　　Baum-Welch模型引數估計公式

　　將這三個式子中的各概率分別簡寫如下：

　　則可將相應的公式寫成：

這三個表示式就是Baum-Welch演算法（Baum-Welch algorithm)，它是EM演算法在隱馬爾可夫模型學習中的具體實現，由Baum和Welch提出。

　　演算法 (Baum-Welch演算法）

　　輸入：觀測資料

　　輸出：隱馬爾可夫模型引數。

　　(1)初始化。對,選取，得到模型。

　　(2)遞推。對

右端各值按觀測和模型計算。

　　(3)終止。得到模型引數。

　　分析：先根據前向演算法得出alpha，根據後向演算法得到beta，之後再根據本文最開始的公式計算gamma和sigamma矩陣，這裡注意gamma是N*N維的，而sigamma是T-1*N*N維的，最後執行Baum-Welch演算法。程式碼裡面有相應的註釋，這裡我也卡了好久，可以先自己到紙上推一下。

def Baum_Welch(pi, A, B, obs_seq, error=0.005):
    switch = 0  # 判斷是否停止迭代
    if not switch:
        N = A.shape[0]  # 可能的狀態個數
        M = B.shape[1]  # 可能的觀測結果個數
        T = len(obs_seq)  # 觀測序列長度
        newB = np.zeros((N, M)) # 初始化觀測概率
        alpha = forward_compute(pi, A, B, obs_seq)[1]   # 前向演算法得到的alpha矩陣  N*T維
        print('alpha:', alpha)
        beta = backword_compute(pi, A, B, obs_seq)[1]   # 後向演算法得到的beta矩陣  N*T維
        print('beta:', beta)
        gamma = np.zeros((N, T))  # gamma_t_i 表示t時刻在狀態q_i的概率 N*N維
        sigamma = np.zeros((T-1, N, N))  # sigamma_t_i_j t時刻處於q_i,t+1時刻處於q_j的概率  (T-1)*N*N維
 
        for t in range(T-1):
            gamma[:, t] = (alpha[:, t]*beta[:, t]) / (alpha[:, t].dot(beta[:, t]))  # 求出gamma矩陣
            denom = np.dot(np.dot(alpha[:,t].T, A) * B[:,obs_seq[t+1]].T, beta[:,t+1])  # sigmma矩陣分母
            for i in range(N):
                molecule = alpha[i, t]* A[i,:] * B[:,obs_seq[t+1]]*beta[:,t+1]  # 分子
                sigamma[t,i,:] = molecule / denom   # 求sigamma
        
        gamma[:, T-1] = (alpha[:, T-1]*beta[:, T-1]) / (alpha[:, T-1].dot(beta[:, T-1]))  # 由於sigamma直到T-1,所以gamma最後要新增一列
        print('gamma:', gamma)
        print('sigamma:', sigamma)
        # print('-----------')
        # print(np.sum(sigamma, axis=0))
        # print('*********')
        # print(np.sum(gamma[:,:T-1], axis=1))
        # print(np.sum(gamma[:,:T-1], axis=1).reshape(N, -1))
        #更新
        newA = np.sum(sigamma, axis=0)/(np.sum(gamma[:,:T-1], axis=1).reshape(N, -1))
        # print(newA)
        # print(obs_seq==0)
        # print(np.sum(gamma, axis=1)
        for m in range(M):
            newB[:,m] = np.sum(gamma.T[obs_seq==m], axis=0)/(np.sum(gamma, axis=1))
        # print(newB)
        newpi = gamma[:, 0] 
    
        # 檢查是否滿足要求
        if np.max(abs(pi - newpi)) < error and np.max(abs(A - newA)) < error and np.max(abs(B - newB)) < error:
                switch = 1
        pi, A, B = newpi, newA, newB
    return A, B, pi

　　之後帶入相關資料進行測試。

A = np.array([[0.1, 0.3, 0.6],[0.3, 0.5, 0.2], [0.3, 0.5, 0.2]])
B = np.array([[0.5, 0.5],[0.5, 0.5], [0.5,0.5]])
pi = np.array([0.2, 0.4, 0.4])

observations_data = np.array([0, 1, 0, 0, 1])

newA, newB, newpi = Baum_Welch(pi, A, B, observations_data)
print("newA: ", newA)
print("newB: ", newB)
print("newpi: ", newpi)

 二、問題3 預測問題  已知模型和觀測序列，求給定序列最大概率下的狀態

　　預測演算法有兩種：近似演算法和維特比演算法。

　　1.近似演算法

　　基本思想：在每個時刻t選擇在該時刻最有可能出現的狀態 i^*_t ，從而得到一個狀態序列 I^* = (i^*₁, i^*₂, ..., i^*_T)。

　　對於給定隱馬爾可夫模型和觀測序列O，在 t 時刻處於狀態 qi 的概率gamma(i) 為：

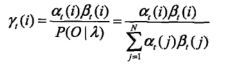
在每一時刻 t 最有可能的狀態 i*t 為：

從而得到狀態序列 I^* = (i^*₁, i^*₂, ..., i^*_T)。

這個程式碼很簡單，直接對gamma按行求最大值就行。

'''
gamma: [[0.2     0.26    0.248   0.2504  0.44992]
        [0.4     0.46    0.448   0.2992  0.24992]
        [0.4     0.28    0.304   0.4504  0.30016]]
'''
def envolution_state(gamma):
    states = []
    for i in range(gamma.shape[1]):
        max_index = np.where(gamma==np.max(gamma[:,i]))[0][0]
        states.append(max_index)
    return states

print('*********test*********')
gamma = np.array([[0.2 ,0.26,0.248,0.2504,0.44992], [0.4,0.46,0.448,0.2992,0.24992], [0.4,0.28,0.304,0.4504,0.30016]])
print('state:', envolution_state(gamma))

　　2、維特比演算法

 　　基本思想：利用動態規劃求解隱馬爾科夫模型預測問題，即用動態規劃求解概率最大路徑（最優路徑），一條路徑對應一個狀態序列。

　　演算法(維特比演算法）

　　輸入：模型和觀測;

　　輸出：最優路徑。

　　⑴初始化

　　(2)遞推。對

　　(3)終止

　　(4)最優路徑回溯。對

求得最優路徑。

def vetebi(pi, A, B, obs_seq):
    N = A.shape[0]  # 狀態個數
    T = len(obs_seq) # 觀測序列長度
    
    deta = np.zeros((N, T))  # 初始化deta矩陣
    fia = np.zeros((N, T), dtype=int)  # 初始化fia矩陣
    path = np.zeros(T, dtype=int)  # 初始化最優路徑
    
    deta[:, 0] = pi*B[:, obs_seq[0]]  # 計算deta_1
    for t in range(1, T):
        matrix = (deta[:, t-1]*A.T)*B[:, obs_seq[t]].reshape(N, -1)  # 計算乘法，deta按列取其中最大的
        deta[:, t] = np.max(matrix, axis=1)  # 給deta賦值
        fia[:, t] = np.argmax(matrix, axis=1)  # 給fia賦值，用於求最優路徑
    print(deta)
    print(fia)
    
    # 最大概率
    P_max = np.max(deta[:, T-1]) 
    # print(P_max)
    
    # 求最優路徑
    path[T-1] = np.max(fia[:, T-1])
    for t in range(T-2, -1, -1):
        path[t] = fia[:, t+1][path[t+1]]
    # print(path)
    return path+1

　　利用書本上例題進行測試。

# test
A = np.array([[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]])
pi = np.array([0.2, 0.4, 0.4])
obs_seq = np.array([0, 1, 0])
path = vetebi(pi, A, B, obs_seq)
print('the best path is :',path)