原題連結：

第一題：複雜連結串列的複製

題目：

輸入一個複雜連結串列（每個節點中有節點值，以及兩個指標，一個指向下一個節點，另一個特殊指標指向任意一個節點），返回結果為複製後複雜連結串列的head。（注意，輸出結果中請不要返回引數中的節點引用，否則判題程式會直接返回空）

解析：

假如這題沒有隨機指標，很好搞，問題是有了隨機指標，如何在新建結點的時候令隨機指標指向正確的位置？可以用一個map來對映原結點和對應的新結點，剛開始的時候不要管隨機指標，按照沒有隨機指標來做，把map填上；這樣搞完後，再遍歷一遍新連結串列，利用map中的對映來確定隨機指標，下面分別給出遞迴做法和非遞迴做法。

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/

class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead)
    {
        map<RandomListNode *, RandomListNode *>
 
 mp;
        RandomListNode *ret = make(pHead, mp);
        for (RandomListNode *p = pHead, *q = ret; p != nullptr; p = p->next, q = q->next)
            q->random = mp[p->random];
        return ret;
    }
    RandomListNode* make(RandomListNode* pHead, map<RandomListNode *, RandomListNode *>
 
 &mp)
    {
        if (pHead == nullptr)
            return nullptr;
        RandomListNode *ret = new RandomListNode(pHead->label);
        mp[pHead] = ret;
        ret->next = make(pHead->next, mp);
        return ret;
    }
};

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/

class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead)
    {
        if (pHead == nullptr)
            return nullptr;
        map<RandomListNode *, RandomListNode *> mp;
        RandomListNode *ret = new RandomListNode(pHead->label), *q = ret;
        mp[pHead] = ret;
        for (auto p = pHead->next; p != nullptr; q->next = new RandomListNode(p->label), mp[p] = q->next, p = p->next, q = q->next);
        q->next = nullptr;
        for (RandomListNode *p = pHead, *q = ret; p != nullptr; p = p->next, q = q->next)
            q->random = mp[p->random];
        return ret;
    }
};

如果不用map這個資料結構該怎麼搞呢？還是要解決原結點和對應新結點之間的對映關係，如何搞？看下面的步驟：

• 每新建一個結點就把該結點插入到原連結串列對應的原結點後；
• 上一步全部完成後，遍歷原連結串列(2倍長度了)，由於原結點和新結點之間是相鄰的，因此只要p->next就可以通過原結點找到對應的新結點，這樣就解決了這個對映關係，這一步確定隨機指標；
• 最後一步就是把加長後的連結串列拆分出來，這樣即保證建立了新連結串列，也保證了原連結串列沒有被破壞。

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/

class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead)
    {
        if (pHead == nullptr)
            return nullptr;
        RandomListNode *p = pHead, *ret = pHead;
        for (; p != nullptr; p = p->next->next) {
            RandomListNode *now = new RandomListNode(p->label);
            now->next = p->next;
            p->next = now;
        }
        for (p = pHead; p != nullptr; p = p->next->next)
            if (p->random != nullptr)
                p->next->random = p->random->next;
        for (p = pHead, ret = p->next; p->next != nullptr;
             pHead = p->next, p->next = p->next->next, p = pHead);
        return ret;
    }
};

第二題：二叉搜尋樹與雙向連結串列

題目：

輸入一棵二叉搜尋樹，將該二叉搜尋樹轉換成一個排序的雙向連結串列。要求不能建立任何新的結點，只能調整樹中結點指標的指向。

解析：

還是分遞迴做法和非遞迴做法。先說遞迴做法。

這裡要引入一個pre指標，它表示上次剛遍歷過的結點的地址；在遞迴的過程中要返回最小的那個結點，由於是中序遍歷，那麼最小的那個結點一定在左子樹(如果有左子樹)；我們只需要修改當前節點的左指標了，pre指向結點的右指標就行了，具體修改如下：

• root->left = pre；
• pre->right = root。

上面兩步操作都建立在root和pre不為空的情況下，具體的邊界可以自己推敲下，或者看我的程式碼，候捷大師說過：“原始碼之前，了無祕密” ，我們都應該多去原始碼中尋找細節，發現祕密。扯遠了，這裡還需要注意一點，按理說還要修改root和下一個結點之間的關係，但是其實這是沒有必要的，當遍歷到下一個結點時，下一個結點就成為了當前結點，root就成為了pre，這個關係會在這裡修改的，所以不需要多此一舉修改root和下一個結點之間的關係。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/  

class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree)
    {
        TreeNode *pre = nullptr;
        return convert(pRootOfTree, &pre);
    }
    TreeNode* convert(TreeNode* pRootOfTree, TreeNode **pre)
    {
        if (pRootOfTree == nullptr)
            return nullptr;
        auto ret = convert(pRootOfTree->left, pre);
        if (ret == nullptr)
            ret = pRootOfTree;
        if (*pre != nullptr)
            (*pre)->right = pRootOfTree;
        pRootOfTree->left = *pre;
        convert(pRootOfTree->right, (*pre = pRootOfTree, pre));
        return ret;
    }
};

非遞迴做法還是利用二叉排序樹中序遍歷的非遞迴寫法，看下這篇部落格；不過還是需要引入pre指標，非遞迴的程式碼其實就是我在中序遍歷的非遞迴寫法上加了點東西就搞定了，思想還是和遞迴做法的一樣。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/  

class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree)
    {
        if (pRootOfTree == nullptr)
            return pRootOfTree;

        typedef TreeNode *pNode;
        stack<pNode> st;
        pNode p = pRootOfTree, ret = nullptr, pre = nullptr;
        for (bool f = true; p || !st.empty(); ) {
            if (p) {
                st.push(p);
                p = p->left;
            } else {
                p = st.top();
                if (f)
                    f = false, ret = p;
                if (pre != nullptr)
                    pre->right = p;
                p->left = pre;
                pre = p;
                st.pop();
                p = p->right;
            }
        }
        return ret;
    }
};

第三題：字串的排列

題目：

輸入一個字串,按字典序打印出該字串中字元的所有排列。例如輸入字串abc,則打印出由字元a,b,c所能排列出來的所有字串abc,acb,bac,bca,cab和cba。

輸入一個字串,長度不超過9(可能有字元重複),字元只包括大小寫字母。

解析：

這題一看，首先必然是利用庫函式next_permutation來做，然後set去重。

關於next_permutation的用法和原始碼可以看下我早年寫的一篇部落格，點這兒， 剛開始寫部落格就寫了這個函式，那個時候沒有過多的解釋原始碼，這個原始碼待會我也會用到，之後會對STL做系統的原始碼閱讀，到時候也會以部落格的形式呈現出來，這裡就不多做解釋了。

class Solution {
public:
    vector<string> Permutation(string str) {
        vector<string> ret;
        if (str.size() == 0)
            return ret;
        set<string> se;
        sort(str.begin(), str.end());
        do {
            se.insert(str);
        } while(next_permutation(str.begin(), str.end()));
        for (auto it = se.begin(); it != se.end(); ret.push_back(*it++));
        return ret;
    }
};

全排列演算法也是我ACM生涯中遇到第一個演算法，當時是求解123456的全排列，我用了dfs，開一個bool型別的used陣列來儲存1到6之間的數字在之前是否出現過；然後從前往後依次去填充。這樣可以保證最後結果一定是字典序的。但是這裡字母可能有重複，沒關係啊，把used的型別改成int型別就行了，裡面儲存的是還有幾個這樣的字母可以用來填充。我一般也喜歡用這個演算法來全排列。

class Solution {
public:
    vector<string> Permutation(string str) {
        vector<string> ret;
        if (str.size() == 0)
            return ret;
        vector<int> cnt(26 * 2, 0);
        for (int i = 0; i < (int)str.size(); ++cnt[mapToIndex(str[i++])]);
        dfs(cnt, ret, "", str.size());
        return ret;
    }

    int mapToIndex(char c)
    {
        return islower(c) ? c - 'a' : c - 'A' + 26;
    }

    void dfs(vector<int> &cnt, vector<string> &ret, string str, int n)
    {
        if (str.size() == n) {
            ret.push_back(str);
            return ;
        }
        for (int i = 0; i < 26 * 2; i++)
            if (cnt[i]) {
                --cnt[i];
                dfs(cnt, ret, str + (char)(i < 26 ? 'a' + i : 'A' + i - 26), n);
                ++cnt[i];
            }
    }
};

這題也有非遞迴的寫法，其實就是我上面提到的next_permutation的實現，模版庫函式中的實現就是非遞迴的，只需要修改下原始碼就行了。

class Solution {
public:
    vector<string> Permutation(string str) {
        typedef string::iterator _BI;
        vector<string> ret;
        _BI _F = str.begin(), _L = str.end();
        _BI _I = _L;
        if (_F == _L)
            return ret;
        if (_F == --_I) {
            ret.push_back(str);
            return ret;
        }
        ret.push_back((sort(_F, _L), str));
        for (bool f = false; !f; _I = _L, --_I) {
            for (; ; ) {
                _BI _Ip = _I;
                if (*--_I < *_Ip) {
                    _BI _J = _L;
                    for (; !(*_I < *--_J); );
                    iter_swap(_I, _J);
                    reverse(_Ip, _L);
                    ret.push_back(str);
                    break;
                }
                if (_I == _F) {
                    reverse(_F, _L);
                    f = true;
                    break;
                }
            }
        }
        return ret;
    }
};

剩下的就是全排列的教科書式演算法了。這個演算法百度都有的，改一下交換條件，如果兩數相等就不交換，因為交換了還是一樣的結果，這樣就重複了。不過要注意的點是如果傳遞給函式的陣列是原陣列，而不是陣列的複製品，那麼是得不到字典序的，雖然全排列的結果是對的；如果採用的是傳遞陣列的複製品，那麼也不要復位的swap，要了也得不到字典序，看下圖，解釋了原因：

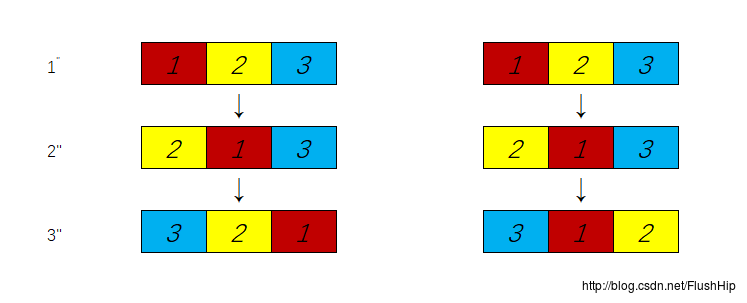
假如你復位了，那麼交換過程中序列就是左邊所示，可以看到，3′′中的21並不是字典序中最小的，故得不到字典序；沒有復位，交換過程中的序列就如右邊所示，可以看到，後兩位一直都是字典序中最小的，這樣才能得到整體字典序。

class Solution {
public:
    vector<string> Permutation(string str) {
        vector<string> ret;
        if (str.size() == 0)
            return ret;
        sort(str.begin(), str.end());
        permutation(str, ret, 0);
        return ret;
    }
    void permutation(string str, vector<string> &ret, unsigned int start)
    {
        if (start == str.size()) {
            ret.push_back(str);
            return ;
        }
        for (unsigned int i = start; i < str.size(); i++) {
            if (i == start || str[i] != str[start]) {
                swap(str[i], str[start]);
                permutation(str, ret, start + 1);
                // swap(str[i], str[start]);
            }
        }
    }
};

第四題：陣列中出現次數超過一半的數字

題目：

陣列中有一個數字出現的次數超過陣列長度的一半，請找出這個數字。例如輸入一個長度為9的陣列{1,2,3,2,2,2,5,4,2}。由於數字2在陣列中出現了5次，超過陣列長度的一半，因此輸出2。如果不存在則輸出0。

解析：

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cnt = 0, flag = 0, i;
        for (i = 0; i < (int)numbers.size(); i++)
            !cnt ? (flag = numbers[i], cnt = 1) : flag == numbers[i] ? ++cnt : --cnt;
        for (cnt = 0, i = 0; i < (int)numbers.size(); cnt += (numbers[i++] == flag));
        return cnt > (int)numbers.size() / 2 ? flag : 0;
    }
};

現在把這個問題改一下，求出陣列中出現次數大於1k的所有數。

首先，我們要確定一點，符合條件的數的個數一定小於k，這個你要承認。 原始問題中，是設一個哨兵，那麼這裡我們就設k - 1個哨兵，遍歷陣列，當前值與這k - 1個哨兵都不相等時，就使其哨兵對應的數量都減一，最後判斷下這k - 1個哨兵到底是不是滿足條件就行了，如何儲存這k - 1個哨兵和其對應的數量呢？用map。

我編寫了 MoreThanK_Num_Solution這個函式來求解這個擴充套件問題，那麼k = 2就是這個擴充套件問題的一個個例，自然原始問題是可以呼叫這個函式的，下面的程式碼在牛客網通過。

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        auto ret = MoreThanK_Num_Solution(numbers, 2);
        return ret.size() == 0 ? 0 : ret[0];
    }

    vector<int> MoreThanK_Num_Solution(vector<int> numbers, int k) {
        map<int, int> mp;
        for (int i = 0; i < (int)numbers.size(); i++) {
            if (mp.find(numbers[i]) != mp.end())
                ++mp[numbers[i]];
            else if (mp.size() < k - 1)
                mp[numbers[i]] = 1;
            else {
                for (auto it = mp.begin(); it != mp.end(); it->second--, ++it);
                for (auto it = mp.begin(); it != mp.end(); !it->second ? it = mp.erase(it) : ++it);
            }
        }
        vector<int> ret;
        for (auto it = mp.begin(); it != mp.end(); ++it) {
            int cnt = 0;
            for (int i = 0; i < (int)numbers.size(); i++)
                cnt += (numbers[i] == it->first);
            if (cnt > (int)numbers.size() / k)
                ret.push_back(it->first);
        }
        return ret;
    }
};

第五題：最小的K個數

題目：

輸入n個整數，找出其中最小的K個數。例如輸入4,5,1,6,2,7,3,8這8個數字，則最小的4個數字是1,2,3,4。

解析：

最簡單的做法就是呼叫sort函式，然後返回前K個元素就可以了。

class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (input.size() < k)
            return ret;
        sort(input.begin(), input.end());
        for (int i = 0; i < k; ret.push_back(input[i++]));
        return ret;
    }
};

既然排序可以做，那麼用multiset(不能用set，set會去重)和priority_queue也是可以做的，一個基於紅黑樹實現，一個基於堆實現。

class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (input.size() < k)
            return ret;
        multiset<int> mse;
        for (auto it = input.begin(); it != input.end(); mse.insert(*it++));
        for (auto it = mse.begin(); k--; ret.push_back(*it++));
        return ret;
    }
};

class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (input.size() < k)
            return ret;
        priority_queue<int, vector<int>, greater<int> > que;
        for (auto it = input.begin(); it != input.end(); que.push(*it++));
        for (; k--; ret.push_back(que.top()), que.pop());
        return ret;
    }
};

這題還可以改進一下，利用快排的原理來做，其實就是把快排的程式碼稍微修改一下，快排的程式碼可以看看這兒。

快排的思想是選定一個基準劃分陣列，使得基準左邊的元素均小於基準，右邊的元素均大於基準，遞迴下去就行了；

那麼是否有必要把整個陣列都劃分完呢，其實沒必要的，具體劃分細節如下：

• 如果左邊元素的個數小於等於k - 1，那麼劃分左邊的全部元素，右邊的元素劃分前k - low + l - 1個就行了；
• 如果左邊的元素個數大於k - 1，那麼劃分左邊前k - 1個元素就行了，右邊的元素不用劃分。

class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (input.size() < k)
            return ret;
        partion(input, k, 0, input.size() - 1);
        for (int i = 0; i < k; ret.push_back(input[i++]));
        return ret;
    }

    void partion(vector<int> &input, int k, int l, int r)
    {
        if (l >= r || k <= 0)
            return ;
        int tmp = input[l], low = l, high = r;
        while (low < high) {
            for (; low < high && tmp < input[high]; high--);
            if (low < high)
                input[low++] = input[high];
            for (; low < high && tmp > input[low]; low++);
            if (low < high)
                input[high--] = input[low];
        }
        input[low] = tmp;
        partion(input, min(low - l, k - 1), l, low);
        partion(input, k - low + l - 1, low + 1, r);
    }
};

第六題：連續子陣列的最大和

題目：

HZ偶爾會拿些專業問題來忽悠那些非計算機專業的同學。今天測試組開完會後,他又發話了:在古老的一維模式識別中,常常需要計算連續子向量的最大和,當向量全為正數的時候,問題很好解決。但是,如果向量中包含負數,是否應該包含某個負數,並期望旁邊的正數會彌補它呢？

例如:{6,-3,-2,7,-15,1,2,2},連續子向量的最大和為8(從第0個開始,到第3個為止)。你會不會被他忽悠住？(子向量的長度至少是1)。

解析：

這題真的是經典，已經不能再經典了，我逐一給出複雜度由高到底的各種演算法，並且給出這個問題的擴充套件問題求出子陣列的左右端點和連續子陣列最大積的解法。

暴力法，先預處理出字首和，然後列舉子陣列的長度和起點，維護一個最大值就行了。

時間複雜度：O(n2)；
空間複雜度：O(n) 。

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        vector<int> sum(array);
        int ret = -0x3f3f3f3f;
        for (int i = 1; i < (int)array.size(); sum[i] = sum[i - 1] + array[i], ++i);
        for (int len = 1; len <= (int)array.size(); ++len)
            for (int i = 0; i + len - 1 < (int)array.size(); ++i)
                ret = max(ret, sum[i + len - 1] - (i ? sum[i - 1] : 0));
        return ret;
    }
};

既然暴力法時間複雜度為O(n2)，那麼有一句話叫只會暴力的O(n2)，會二分的O(nlogn)，會動態規劃的O(n)，會數學的就O(1)。那麼這個題我們是不是可以也二分搞一下然後優化到O(nlogn)呢？答案是可以的。

考慮一下這個最大和的子陣列會在陣列中的什麼位置呢？答案無非就是下面三種情況：

• 位置在陣列中點的左邊；
• 位置在陣列中點的右邊；
• 位置跨過中點，中點的兩邊都有。

情況一、二都可以遞迴解決，問題是情況三怎麼搞？如果是情況三，那麼只需要開兩個迴圈分別從中點的左邊和右邊維護下靠近中點的連續陣列的最大和就行了。

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        return dfs(array, 0, array.size());
    }

    int dfs(vector<int> &array, int l, int r)
    {
        if (r - l == 1)
            return array[l];
        int mid = (r + l) / 2, ll = dfs(array, l, mid), rr = dfs(array, mid, r);
        int left = -0x3f3f3f3f, right = left, sum = 0, i;
        for (i = mid - 1; i >= l; left = max(left, sum += array[i--]));
        for (i = mid, sum = 0; i < r; right = max(right, sum += array[i++]));
        return max(max(ll, rr), left + right);
    }
};

上面的這個程式碼還能不能優化呢，可以的，在dfs中，這兩個for迴圈其實可以預處理出來，這樣，dfs的時間複雜度就為O(logn)，但是預處理的時間為O(n)，所以整體的複雜度為O(n)。

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        vector<int> sum_l(array), sum_r(array);
        for (int i = 1; i < (int)array.size(); sum_l[i] = max(array[i], sum_l[i - 1] + array[i]), i++);
        for (int i = (int)array.size() - 2; i >= 0; sum_r[i] = max(array[i], sum_r[i + 1] + array[i]), i--);
        return dfs(array, 0, array.size(), sum_l, sum_r);
    }

    int dfs(vector<int> &array, int l, int r, vector<int> &sum_l, vector<int> &sum_r)
    {
        if (r - l == 1)
            return array[l];
        int mid = (r + l) / 2, ll = dfs(array, l, mid, sum_l, sum_r), rr = dfs(array, mid, r, sum_l, sum_r);
        <