卷積

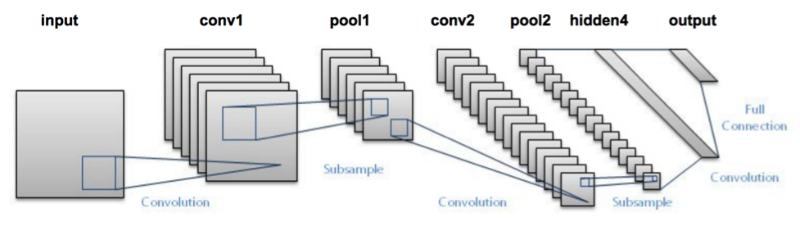
卷積神經網路的結構

其中,input為輸入,conv為卷積層,由卷積核構成,pool為池層,由池化函式構成最後是全連線層與輸出層,其負責對卷積層提取的特徵進行處理以獲得我們需要的結果

卷積函式

卷積函式是本篇文章要講解的內容,在TensorFlow中卷積函式輸入的引數其輸入引數
主要有input, filter, strides, padding, use_cudnn_on_gpu=None,data_format=None, name=None)
其中
1. input 為輸入,一個張量Tensor ,資料型別必須為float32 或者 float64
2. filter 為卷積核,輸入型別必須與input一樣
3. padding為一個字串取值 SAME為補零使輸入輸出的影象大小相同,取值VALLD則允許輸入輸出的影象大小不一致
4. name,可選,字串,用於視覺化中,為該操作起一個名字
5. strides 是另外一個極其重要的引數,其為一個長度為4 的一維整數型別陣列,每一位對應input中每一位對應的移動步長

Input

Input的張量維度:[batch,in_height,in_width,in_channels],例如mnist中的輸入影象為 28 * 28 的黑白影象,其張量即為[batch,28,28,1],1代表黑白,RGB彩色影象的通道則為3,而batch 則為輸入的影象數量,一次輸入10張圖片時,其為10,20張時則為20

filter 卷積核

filter 即為CNN中的卷積核，以我們最常用的tf.nn.conv2d為例 .它要求是一個Tensor，具有[filter_height, filter_width, in_channels, out_channels]這樣的shape，(其他的卷積函式其Tensor的具體內容是不一樣的,在使用時請注意他們的不同)
tf.nn.conv2d中[filter_height, filter_width, in_channels, channel_multiplierl] 含義為[卷積核的高度，卷積核的寬度，影象通道數，卷積核個數]，要求型別與引數input相同，有一個地方需要注意，第三維in_channels，就是引數input的第四維.

在使用中,因為一般不對Input的第一維和第四維進行卷積操作,所以strides 一般為[1,X,X,1]

strides

正如前面所述,strides 是另外一個極其重要的引數,其為一個長度為4 的一維整數型別陣列,每一位對應input中每一位對應的移動步長.
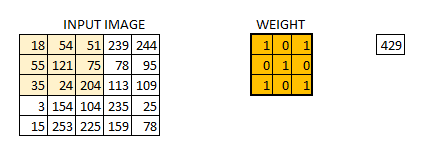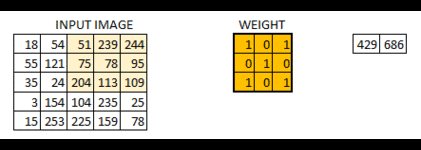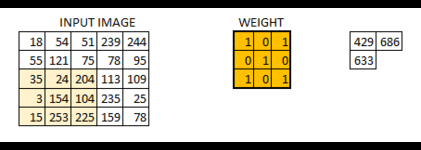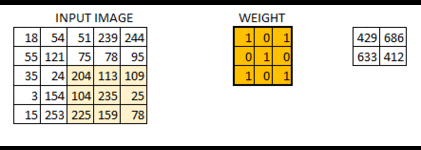
步長為一的卷積操作,不補零:

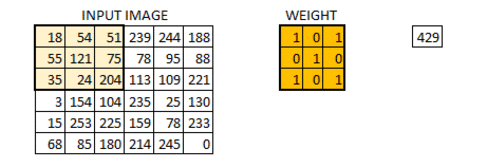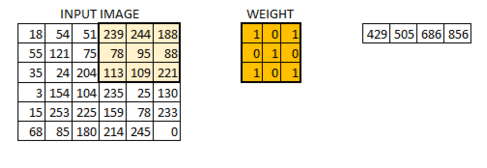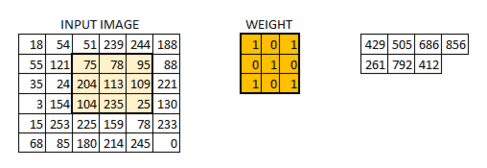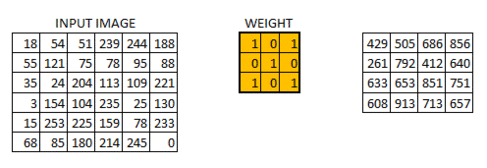
步長為二的卷積操作,不補零:

padding 與步長

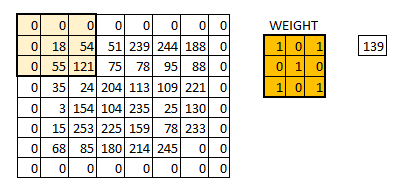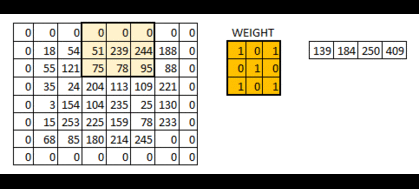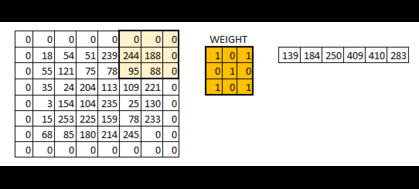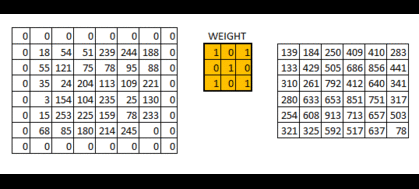
padding=’SAME’ 時,TensorFlow會自動對原影象進行補零,從而使輸入輸出的影象大小一致
效果如下:

padding=’VALLLD’ 時,則會縮小原影象的大小.

輸入輸出影象大小的計算

此段內容引自我翻譯的一篇

1. 過濾器的數量 ——輸出音量的深度就等於濾波器應用的數量。 每個濾波器(卷積核)可以輸出一個圖片,卷積核增加,輸出圖片的數量增加
   
2. 步長 ——控制著卷積核向下移動的畫素值。 高步值長時我們跨過的畫素值,因此產生較小的輸出量。
3. 補零 ——這有助於我們保持輸入影象的大小。 如果只在原始影象周圍新增一個補零的層數,並且步長為一,那麼輸出將保留原始影象的大小。

我們可以應用一個簡單的公式來計算輸出尺寸。 輸出影象的空間大小可以計算(W-F + 2 p / S)+ 1。 這裡,W是輸入圖片大小,F是卷積核的大小,P是填充應用的數量和S是步長的數量。 假設我們有一個輸入影象的大小32 * 32 * 3,我們應用10過濾器的大小3 * 3 * 3,與單步和補零。

W = 32,F = 3,P = 0和S = 1。 輸出深度等於過濾器應用的數量即10。

輸出音量的大小將(32-3 + 0)/ 1 + 1 = 30。 因此,輸出音量將30 * 30 * 10。

TensorFlow中常用的卷積函式

tf.nn.conv2d

tf.nn.conv2d:對一個思維的輸入資料 input 和四維的卷積核filter 進行操作,然後對輸入的資料進行二維的卷積操作,得到卷積之後的結果,也是我們最常用的卷積函式

示例程式碼:

input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 2), dtype=np.float32)
y = tf.nn.conv2d(input_data, filter_data, strides=[1, 1, 1, 1], padding='SAME')

print('tf.nn.conv2d : ', y)
# tf.nn.conv2d :  Tensor("Conv2D:0", shape=(10, 9, 9, 2), dtype=float32)
# 在padding='SAME'時輸入輸出的影象大小是一致的

tf.nn.depthwise_conv2d

1. input 的資料維度 [batch ,in_height,in_wight,in_channels]
2. 卷積核的維度是 [filter_height,filter_heught,in_channel,channel_multiplierl]
3. 講不通的卷積和獨立的應用在in_channels 的每一個通道上(從通道 1 到通道channel_multiplier)
4. 然後將所有結果進行彙總,輸出通道的總數是,in_channel * channel_multiplier

程式碼如下

input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 2), dtype=np.float32)

y = tf.nn.depthwise_conv2d(input_data, filter_data, strides=[1, 1, 1, 1], padding='SAME')
print('tf.nn.depthwise_conv2d : ', y)

# tf.nn.depthwise_conv2d :  Tensor("depthwise:0", shape=(10, 9, 9, 6), dtype=float32)
# 輸出的通道數增加了

其效果類似於多個卷積核運算都是張量的一個維度增加,不同之處在於通道數的增加是卷積核在不同通道上運算的結果,而多個卷積核運算是batch的數量增加

完整的示例CODE

# - * - coding: utf - 8 -*-
import tensorflow as tf
import os
import numpy as np

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# tf.nn.convolution
# 計算N維卷積的和

input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 2), dtype=np.float32)
y = tf.nn.convolution(input_data, filter_data, strides=[1, 1], padding='SAME')

print('1. tf.nn.convolution : ', y)
# 1. tf.nn.convolution :  Tensor("convolution:0", shape=(10, 9, 9, 2), dtype=float32)


# tf.nn.conv2d
# 對一個思維的輸入資料 input 和四維的卷積核filter 進行操作,然後對輸入的資料進行二維的卷積操作,得到卷積之後的結果
input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 2), dtype=np.float32)
y = tf.nn.conv2d(input_data, filter_data, strides=[1, 1, 1, 1], padding='SAME')

print('2. tf.nn.conv2d : ', y)
#2. tf.nn.conv2d :  Tensor("Conv2D:0", shape=(10, 9, 9, 2), dtype=float32)

# tf.nn.depthwise_conv2d
# input 的資料維度 [batch ,in_height,in_wight,in_channels]
# 卷積核的維度是 [filter_height,filter_heught,in_channel,channel_multiplierl]
# 講不通的卷積和獨立的應用在in_channels 的每一個通道上(從通道 1 到通道channel_multiplier)
# 然後將所有結果進行彙總,輸出通道的總數是,in_channel * channel_multiplier

input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 2), dtype=np.float32)

y = tf.nn.depthwise_conv2d(input_data, filter_data, strides=[1, 1, 1, 1], padding='SAME')
print('3. tf.nn.depthwise_conv2d : ', y)

# tf.nn.separable_conv2d
# 利用幾個分離的卷積核去做卷積,在該函式中,將應用一個二維的卷積核,在每個通道上,以深度channel_multiplier進行卷積
input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
depthwise_filter = tf.Variable(np.random.rand(2, 2, 3, 5), dtype=np.float32)
poinwise_filter = tf.Variable(np.random.rand(1, 1, 15, 20), dtype=np.float32)
# out_channels >= channel_multiplier * in_channels
y = tf.nn.separable_conv2d(input_data, depthwise_filter=depthwise_filter, pointwise_filter=poinwise_filter,
                           strides=[1, 1, 1, 1], padding='SAME')
print('4. tf.nn.separable_conv2d : ', y)

# 計算Atrous卷積,又稱孔卷積或者擴張卷積
input_data = tf.Variable(np.random.rand(1, 5, 5, 1), dtype=np.float32)
filters = tf.Variable(np.random.rand(3, 3, 1, 1), dtype=np.float32)
y = tf.nn.atrous_conv2d(input_data, filters, 2, padding='SAME')
print('5. tf.nn.atrous_conv2d : ', y)

# 在解卷積網路(deconvolutional network) 中有時被稱為'反捲積',但實際上是conv2d的轉置,而不是實際的反捲積
x = tf.random_normal(shape=[1, 3, 3, 1])
kernal = tf.random_normal(shape=[2, 2, 3, 1])
y = tf.nn.conv2d_transpose(x, kernal, output_shape=[1, 5, 5, 3], strides=[1, 2, 2, 1], padding='SAME')
print('6. tf.nn.conv2d_transpose : ', y)

# 與二維卷積類似,用來計算給定三維輸入和過濾器的情況下的一維卷積.
# 不同的是,它的輸入維度為 3,[batch,in_width,in_channels].
# 卷積核的維度也是三維,[filter_height,in_channel,channel_multiplierl]
# stride 是一個正整數,代表一定每一步的步長
input_data = tf.Variable(np.random.rand(1, 5, 1), dtype=np.float32)
filters = tf.Variable(np.random.rand(3, 1, 3), dtype=np.float32)
y = tf.nn.conv1d(input_data, filters, stride=2, padding='SAME')
print('7. tf.nn.conv1d : ', y)

# 與二維卷積類似,用來計算給定五維輸入和過濾器的情況下的三維卷積.
# 不同的是,它的輸入維度為 5,[batch,in_depth,in_height,in_width,in_channels].
# 卷積核的維度也是三維,[filter_depth,filter_height,in_channel,channel_multiplierl]
# stride 相較二維卷積多了一維,變為[strides_batch,strides_depth,strides_height,strides_width,strides_channel],必須保證strides[0] = strides[4] =1
input_data = tf.Variable(np.random.rand(1, 2, 5, 5, 1), dtype=np.float32)
filters = tf.Variable(np.random.rand(2, 3, 3, 1, 3), dtype=np.float32)
y = tf.nn.conv3d(input_data, filters, strides=[1, 2, 2, 1, 1], padding='SAME')
print('8. tf.nn.conv3d : ', y)

# 與conv2d_transpose 二維反捲積類似
# 在解卷積網路(deconvolutional network) 中有時被稱為'反捲積',但實際上是conv3d的轉置,而不是實際的反捲積
x = tf.random_normal(shape=[2, 1, 3, 3, 1])
kernal = tf.random_normal(shape=[2, 2, 2, 3, 1])
y = tf.nn.conv3d_transpose(x, kernal, output_shape=[2, 1, 5, 5, 3], strides=[1, 2, 2, 2, 1], padding='SAME')
print('9. tf.nn.conv3d_transpose : ', y)

RUN

1. tf.nn.convolution :  Tensor("convolution:0", shape=(10, 9, 9, 2), dtype=float32)
2. tf.nn.conv2d :  Tensor("Conv2D:0", shape=(10, 9, 9, 2), dtype=float32)
3. tf.nn.depthwise_conv2d :  Tensor("depthwise:0", shape=(10, 9, 9, 6), dtype=float32)
4. tf.nn.separable_conv2d :  Tensor("separable_conv2d:0", shape=(10, 9, 9, 20), dtype=float32)
5. tf.nn.atrous_conv2d :  Tensor("convolution_1/BatchToSpaceND:0", shape=(1, 5, 5, 1), dtype=float32)
6. tf.nn.conv2d_transpose :  Tensor("conv2d_transpose:0", shape=(1, 5, 5, 3), dtype=float32)
7. tf.nn.conv1d :  Tensor("conv1d/Squeeze:0", shape=(1, 3, 3), dtype=float32)
8. tf.nn.conv3d :  Tensor("Conv3D:0", shape=(1, 1, 3, 5, 3), dtype=float32)
9. tf.nn.conv3d_transpose :  Tensor("conv3d_transpose:0", shape=(2, 1, 5, 5, 3), dtype=float32)