Tensorflow手寫數字識別之簡單神經網路分類與CNN分類效果對比
用Tensorflow進行深度學習和人工智慧具有開發簡單,建模速度快,準確度高的優點。作為學習影象識別分類的入門,手寫輸入數字識別是個很好的例子。
MNIST包中共有60000個手寫數字筆跡灰度影象作為訓練集,每張手寫數字筆跡圖片均已儲存為28*28畫素,同時還有一個label集對這60000個訓練影象一一標識。此外,還有一個測試集,包括10000張新的手寫筆記灰度影象,以及一個對應10000張圖片的標記。通過使用60000張訓練集圖片及label集分別建立簡單的MNIST模型和CNN卷積神經網路模型,而後使用10000張測試圖片及對應的label集對比不同模型效果。
A. 建立簡單神經網路模型步驟如下:
1. 鑑於每張圖片解析度為28*28畫素,即28行28列個數據,對於簡單MNIST模型,這樣的資料結構還過於複雜,若將影象中所有畫素的二維關係轉化為一維關係,模型建立和訓練將會很簡單。為將該圖片中的所有畫素序列化,即將該圖片格式變為一行784列(1*784的結構)。對於模型的輸出,可使用一個一行十列的結構,表示該模型分析手寫圖片後對應數字0~9的概率,概率最大者為1,其餘9個為0。假設輸入影象為n,則輸入資料集可表示為一個二維張量[n, 784],對於輸出,使用[n, 10]的二維張量。程式中使用佔位符placeholder表示,張數引數n使用None佔位,由具體輸入的影象張數初始化。
#define place holder for inputs to network
xs =tf.placeholder(tf.float32, [None,784])#28*28
ys =tf.placeholder(tf.float32, [None,10])
2. 新增中間層網路。可使用Y =XW + b的定義中間層模型,X表示輸入的資料集(為[n,784]的二維張量); W為weight權重張量,為[784, 10]的張量,XW做矩陣乘法後得到[n, 10]的張量; b為bias量,維度為[1,10]; Y為預測結果張量,該結果張量還需要使用激勵函式處理,以拉開預測各數字概率,提高預測正確性,本程式中使用tf.nn.
def add_layer(inputs,in_size, out_size, activation_function=None):
#add one morelayer and return the output of this layer
W = tf.Variable(tf.random_normal([in_size,out_size]))
b = tf.Variable(tf.zeros([1,out_size])+0.1)
Wb = tf.matmul(inputs, W)+b
if activation_functionis None
outputs = Wb
else:
outputs = activation_function(Wb)
return outputs
3. 建立並定義網路。首先定義prediction張量,其值為新增中間層網路的返回張量。之後計算交叉熵cross_entropy,並使用梯度下降優化器GradientDescentOptimizer對交叉熵處理並訓練得到張量train_step。
#add output layer
prediction= add_layer(xs, 784, 10,activation_function= tf.nn.softmax)
#the error between prediction and real data
cross_entropy= tf.reduce_mean(-tf.reduce_sum(ys* tf.log(prediction),reduction_indices=[1]))#loss
train_step= tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
4. 訓練網路,首先要對所有變數初始化,之後,每次從訓練集中隨機去除100個樣本訓練網路,總共訓練1001次得到訓練模型
with tf.Session()assess:
if int((tf.__version__).split('.')[1]) <12andint((tf.__version__).split('.')[0])<1:
init =tf.initialize_all_veriables()
else:
init =tf.global_variables_initializer()
print(tf.__version__) sess.run(init)
for i inrange(1001):
batch_xs, batch_ys =mnist.train.next_batch(100)
sess.run(train_step, feed_dict = {xs: batch_xs, ys: batch_ys})
5. 計算模型準確性,演算法如下,v_xs為輸入的測試影象集,v_ys為輸入測試影象對應的label集。依據輸入v_xs計算出的預測結果集為y_pre將與v_ys這個label集進行對比,如果相同則判斷正確,否則為錯誤,計算出的正確結果儲存在correct_prediction 中。之後將correct_prediction張量轉換為float32格式,並求均值得到正確率。
def compute_accuracy(v_xs,v_ys):
global prediction
y_pre = sess.run(prediction, feed_dict= {xs:v_xs})
correct_prediction = tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
accuracy =tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
result = sess.run(accuracy, feed_dict= {xs: v_xs, ys:v_ys})
return result
B. 建立CNN模型步驟如下:
1. 對於CNN網路,無需將影象轉換為一維張量,保持其28*28*1(1為影象的channel數,灰度影象為1,彩色影象為3)的樣式進行卷積,卷積後,影象將被變為28*28*32的張量。
2. 定義卷積核。卷積核為[5,5,1,32]的思維張量,該卷積核為5*5的大小,輸入size為1,輸出size為32
def kernel_variable(shape):
initial = tf.truncated_normal(shape=shape,stddev=0.1)
return tf.Variable(initial)
w_conv1 = kernel_variable([5,5,1,32])
3. 定義bias偏量,其輸出size為32
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
b_conv1 = bias_variable([32])
4. 構建兩層卷積層,每層卷積的輸出層均被relu激勵函式處理,而後池化,作為下一層網路的輸入。第一層卷積層處理後將n*28*28*1的影象集轉換為n*28*28*32的維度,經歷池化後變為n*14*14*32。第二層卷積層將第一層卷積層的輸出由n*14*14*32變為n*14*14*64,經歷池化後變為n*7*7*64維度。
# conv1 layer
w_conv1= kernel_variable([5,5,1,32]) #kernel 5*5, insize 1, out size 32
b_conv1= bias_variable([32])
h_conv1= tf.nn.relu(conv2d(x_image, w_conv1)+b_conv1) #output size 28*28*32
h_pool1= max_pool_2x2(h_conv1) #output size 14*14*32
# conv2 layer
w_conv2= kernel_variable([5,5,32,64]) #kernel 5*5, insize 32, out size 64
b_conv2= bias_variable([64])
h_conv2= tf.nn.relu(conv2d(h_pool1, w_conv2)+ b_conv2) #outputsize 14*14*64
h_pool2= max_pool_2x2(h_conv2) #output size 7*7*64
5. 建立兩層神經網路預測結果。第一層神經網路現將第二次池化後的n*7*7*64的四維張量輸入影象轉換為n*3136的二維張量,3136是將7*7*64三維的資料轉換為一維,之後該n*3136的張量與weight權重矩陣([3136,1024] 的張量)相乘得到n*1024的二維張量輸出給第二層網路層。為了應對過擬合,使用dropout以0.5的概率故意丟棄部分網路節點以提高網路適應性。第二層網路層權重矩陣為1024*10,與第一次輸出結果相乘後得到n*10的結果集合。對於一對一的輸出結果,可採用sigmod處理,對於一對多的輸出,如本例,採用softmax。
# fc1 layer
w_fc1= kernel_variable([7*7*64,1024])
b_fc1= bias_variable([1024])
h_pool2_flat= tf.reshape(h_pool2, [-1,7*7*64])
h_fc1= tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1)+b_fc1)
h_fc1_drop= tf.nn.dropout(h_fc1, keep_prob)
# fc2 layer
w_fc2= kernel_variable([1024,10])
b_fc2= bias_variable([10])
prediction_CNN= tf.nn.softmax(tf.matmul(h_fc1_drop,w_fc2)+b_fc2)
6.訓練CNN網路。首先初始化所有變數。而後從訓練集中每次取出100張圖片和label訓練網路,共訓練1000次。
cross_entropy_CNN = tf.reduce_mean(-tf.reduce_sum(ys*tf.log(prediction_CNN),reduction_indices=[1]))#loss
train_step_CNN = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy_CNN)
with tf.Session()assess:
if int((tf.__version__).split('.')[1]) <12andint((tf.__version__).split('.')[0])<1:
init =tf.initialize_all_veriables()
else:
init =tf.global_variables_initializer()
print(tf.__version__)
sess. run(init)
for i in range(1001):
batch_xs, batch_ys =mnist.train.next_batch(100)
sess.run(train_step_CNN, feed_dict={xs: batch_xs,ys: batch_ys, keep_prob:0.5})
7.計算模型準確性,演算法如下,v_xs為輸入的測試影象集,v_ys為輸入測試影象對應的label集。依據輸入v_xs計算出的預測結果集為y_pre將與v_ys這個label集進行對比,如果相同則判斷正確,否則為錯誤,計算出的正確結果儲存在correct_prediction 中。之後將correct_prediction張量轉換為float32格式,並求均值得到正確率。
def compute_accuracy(v_xs, v_ys):
global prediction_CNN
y_pre = sess.run(prediction_CNN,feed_dict= {xs:v_xs})
correct_prediction =tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
accuracy =tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
result = sess.run(accuracy, feed_dict= {xs: v_xs,ys:v_ys})
return result
8.每訓練100次,使用測試集對網路當前訓練結果進行檢測,列印預測正確率。
for i inrange(1001):
batch_xs, batch_ys =mnist.train.next_batch(100)
sess.run(train_step, feed_dict = {xs: batch_xs,ys: batch_ys})
sess.run(train_step_CNN, feed_dict={xs: batch_xs,ys: batch_ys, keep_prob:0.5})
if i%100==0:
print('correctness: ', i,' is ',compute_accuracy(mnist.test.images, mnist.test.labels))
print('correctness_CNN: ', i,' is ',compute_accuracy_CNN(mnist.test.images, mnist.test.labels))
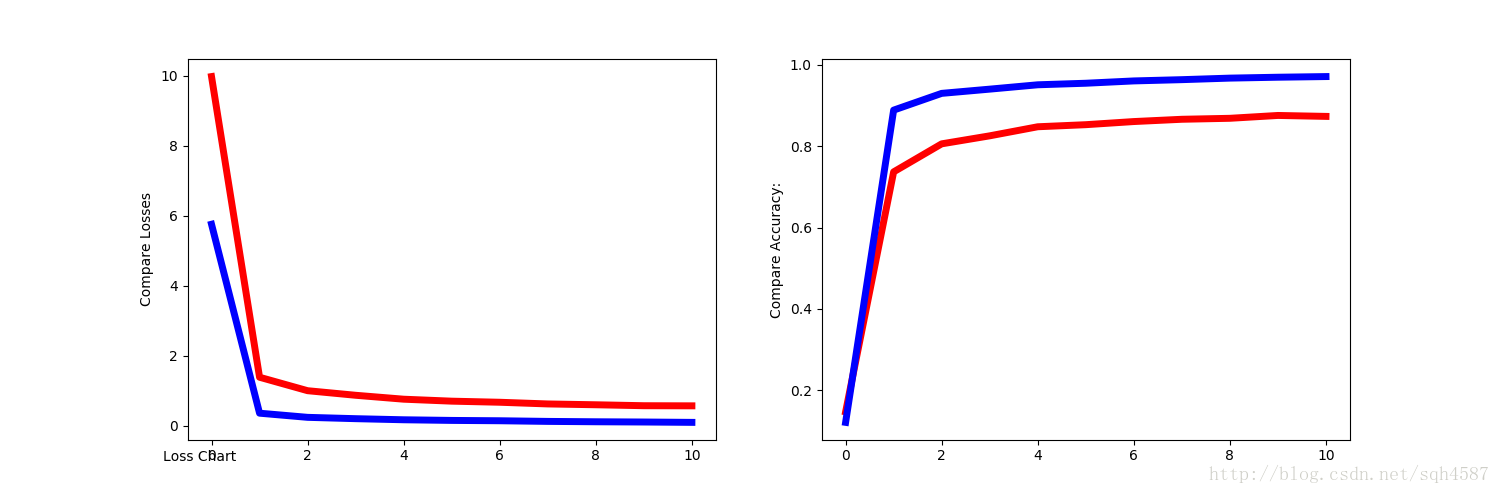
C. 結果對比如下:如下圖可見,CNN網路準確性隨著訓練次數增加而提升,最後能打奧0.9683的準確度(完全正確為1),而簡單MNIST在訓練到800次時出現過擬合,準確率從最高的0.8692降到了0.098。我的電腦比較老,i5 (2410M)的CPU,8G記憶體,訓練大約需要15分鐘,對CPU使用率要求較高,記憶體在CNN網路訓練時佔用量較大。
途中紅線為普通神經網路結果,藍線為CNN網路結果,由左圖可見,兩種方法的loss都在隨著訓練次數的增加而降低,但是CNN能夠更接近0,表現更出眾,而預測精度也是類似,普通網路能達到約87%的正確率,但CNN網路可以達到97%,精度提升顯著。每輪的計算結果如下:
correctness: 0 is 0.147100001574
correctness_CNN: 0 is 0.12120000273
loss: 0 is 9.97904
loss_CNN: 0 is 5.7561
correctness: 100 is 0.73710000515
correctness_CNN: 100 is 0.888899981976
loss: 100 is 1.38197
loss_CNN: 100 is 0.353873
correctness: 200 is 0.805999994278
correctness_CNN: 200 is 0.930100023746
loss: 200 is 0.997057
loss_CNN: 200 is 0.235152
correctness: 300 is 0.825699985027
correctness_CNN: 300 is 0.940500020981
loss: 300 is 0.866042
loss_CNN: 300 is 0.196917
correctness: 400 is 0.847999989986
correctness_CNN: 400 is 0.951200008392
loss: 400 is 0.753898
loss_CNN: 400 is 0.165623
correctness: 500 is 0.853100001812
correctness_CNN: 500 is 0.954999983311
loss: 500 is 0.697782
loss_CNN: 500 is 0.147157
correctness: 600 is 0.860800027847
correctness_CNN: 600 is 0.960699975491
loss: 600 is 0.666501
loss_CNN: 600 is 0.137592
correctness: 700 is 0.866400003433
correctness_CNN: 700 is 0.963800013065
loss: 700 is 0.618222
loss_CNN: 700 is 0.119138
correctness: 800 is 0.868799984455
correctness_CNN: 800 is 0.967599987984
loss: 800 is 0.59465
loss_CNN: 800 is 0.108558
correctness: 900 is 0.875800013542
correctness_CNN: 900 is 0.969799995422
loss: 900 is 0.567654
loss_CNN: 900 is 0.101511
correctness: 1000 is 0.87349998951
correctness_CNN: 1000 is 0.971400022507
loss: 1000 is 0.564226
loss_CNN: 1000 is 0.0913478
D. 完整程式碼如下:
from __future__ import print_function
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import os
import numpy as np
import matplotlib.pyplot as plt
MODEL_SAVE_PATH="my_net/"
MODEL_NAME="save_net.ckpt"
#number 1 to 10 data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
def add_layer(inputs, in_size, out_size, activation_function=None):
#add one more layer and return the output of this layer
W = tf.Variable(tf.random_normal([in_size, out_size]))
b = tf.Variable(tf.zeros([1,out_size])+0.1)
Wb = tf.matmul(inputs, W)+b
if activation_function is None:
outputs = Wb
else:
outputs = activation_function(Wb)
return outputs
def compute_accuracy(v_xs, v_ys):
global prediction
y_pre = sess.run(prediction, feed_dict = {xs:v_xs})
correct_prediction = tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
result = sess.run(accuracy, feed_dict = {xs: v_xs, ys:v_ys})
return result
def compute_accuracy_CNN(v_xs, v_ys):
global prediction_CNN
y_pre = sess.run(prediction_CNN, feed_dict = {xs:v_xs, keep_prob:1})
correct_prediction = tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
result = sess.run(accuracy, feed_dict = {xs: v_xs, ys:v_ys, keep_prob:1})
return result
def kernel_variable(shape):
initial = tf.truncated_normal(shape=shape, stddev = 0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x,W):
#stride [1, x_movement, y_movement,1]
#stride[0] and stride[3] must be 1
return tf.nn.conv2d(x, W, strides = [1,1,1,1], padding = 'SAME')
def max_pool_2x2(x):
# stride [1, x_movement, y_movement,1]
return tf.nn.max_pool(x, ksize= [1,2,2,1], strides=[1,2,2,1], padding='SAME')
#define place holder for inputs to network
xs = tf.placeholder(tf.float32, [None, 784]) #28*28
ys = tf.placeholder(tf.float32, [None, 10])
keep_prob = tf.placeholder(tf.float32)
x_image = tf.reshape(xs, [-1,28,28,1])
# conv1 layer
w_conv1 = kernel_variable([5,5,1,32]) #kernel 5*5, in size 1, out size 32
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1)+b_conv1) #output size 28*28*32
h_pool1 = max_pool_2x2(h_conv1) #output size 14*14*32
# conv2 layer
w_conv2 = kernel_variable([5,5,32,64]) #kernel 5*5, in size 32, out size 64
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2)+ b_conv2) #output size 14*14*64
h_pool2 = max_pool_2x2(h_conv2) #output size 7*7*64
# fc1 layer
w_fc1 = kernel_variable([7*7*64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1,7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1)+b_fc1)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# fc2 layer
w_fc2 = kernel_variable([1024,10])
b_fc2 = bias_variable([10])
prediction_CNN = tf.nn.softmax(tf.matmul(h_fc1_drop,w_fc2)+b_fc2)
#add output layer
prediction = add_layer(xs, 784, 10, activation_function= tf.nn.softmax)
#the error between prediction and real data
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys* tf.log(prediction), reduction_indices=[1])) #loss
cross_entropy_CNN = tf.reduce_mean(-tf.reduce_sum(ys* tf.log(prediction_CNN), reduction_indices=[1])) #loss
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
train_step_CNN = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy_CNN)
saver = tf.train.Saver() # define a saver for saving and restoring
Total_test_loss = np.zeros((int(1001/100)+1), float)
Total_test_loss_CNN = np.zeros((int(1001/100)+1), float)
Total_test_acc = np.zeros((int(1001/100)+1), float)
Total_test_acc_CNN = np.zeros((int(1001/100)+1), float)
count =0
with tf.Session() as sess:
if int((tf.__version__).split('.')[1]) <12 and int((tf.__version__).split('.')[0])<1:
init = tf.initialize_all_veriables()
else:
init = tf.global_variables_initializer()
print(tf.__version__)
sess. run(init)
for i in range(1001):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict = {xs: batch_xs, ys: batch_ys})
sess.run(train_step_CNN, feed_dict={xs: batch_xs, ys: batch_ys, keep_prob: 0.5})
if i%100 ==0:
Total_test_acc[count] = compute_accuracy(mnist.test.images, mnist.test.labels)
Total_test_acc_CNN[count] = compute_accuracy_CNN(mnist.test.images, mnist.test.labels)
print('correctness: ', i, ' \tis \t', Total_test_acc[count])
print('correctness_CNN: ', i, ' \tis \t', Total_test_acc_CNN[count])
loss = sess.run(cross_entropy, feed_dict={xs: mnist.test.images, ys: mnist.test.labels, keep_prob: 1.0})
loss_CNN = sess.run(cross_entropy_CNN,
feed_dict={xs: mnist.test.images, ys: mnist.test.labels, keep_prob: 1.0})
print('loss: ', i, ' \tis \t', loss)
print('loss_CNN: ', i, ' \tis \t', loss_CNN)
Total_test_loss[count] = loss
Total_test_loss_CNN[count] = loss_CNN
count += 1
saver.save(sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME), write_meta_graph=False)
# plotting
plt.figure(1, figsize=(15, 5))
plt.subplot(121)
# plt.scatter(x, y)
plt.ylabel('Compare Losses')
plt.plot(Total_test_loss, 'r-', lw=5)
plt.plot(Total_test_loss_CNN, 'b-', lw=5)
plt.text(-1, -1, 'Loss Chart')
plt.subplot(122)
# plt.scatter(x, y)
plt.ylabel('Compare Accuracy:')
plt.plot(Total_test_acc, 'r-', lw=5)
plt.plot(Total_test_acc_CNN, 'b-', lw=5)
plt.text(-1, -1, 'Accuracy Chart')
plt.show()