ECC加密演算法
關鍵詞:
ECC:Elliptic Curve Cryptography (ECC)
基於離散對數的橢圓曲線密碼系統提供與RSA類似的安全性,但是具有相對較短的金鑰大小。
GF(p) 上的橢圓曲線
素數 p > 3,並且 a,b ∈ GF(p),在 GF(p) 上使得4a3+ 27b2 ≠ 0 。
在GF(p)上,帶引數a和b的橢圓曲線 E 被定義為(x,y)的解集,其中 x, y ∈ GF(p) 滿足如下方程:
y2= x3 + ax + b
以及一個額外的點 O。點的集合 E 形成一個組,並遵守以下規則:
- O + O = O
- (x, y) + O = (x,y)
- (x, y) + (x, -y) = O
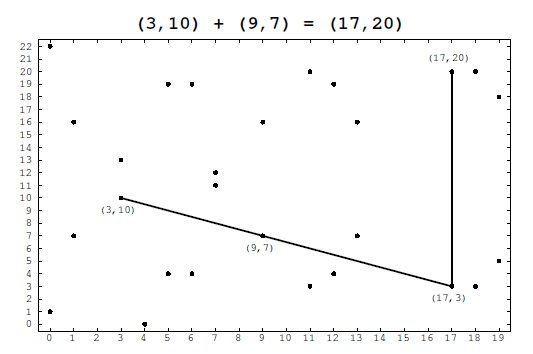
- 兩個不相等的點相加,x1, ≠ x2:
λ = (y2 - y1) (x2- x1)-1
x3 = λ2 - x1-x2
y3= λ(x1- x3- 一個點的2倍,x1, ≠ 0 :
(x1, y1) + (x1, y1)= (x3, y3)
λ = (3x12 + a) (2y1)-1
x3 = λ2 - 2x1
y3 = λ(x1 - x3) - y1
集合 E 是 滿足:y2 mod p = (x3 + ax + b) mod p
例子:
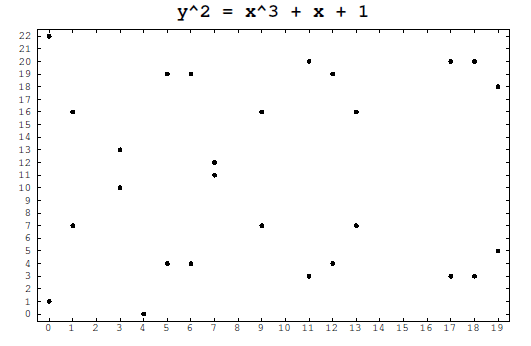
假設 a = 1, b = 1, p = 23,則橢圓曲線 E23(1, 1) 上的點如下:
| (0,1) | (6,4) | (12,19) |
| (0,22) | (6,19) | (13,7) |
| (1,7) | (7,11) | (13,16) |
| (1,16) | (7,12) | (17,3) |
| (3,10) | (9,7) | (17,20) |
| (3,13) | (9,16) | (18,3) |
| (4,0) | (11,3) | (18,20) |
| (5,4) | (11,20) | (19,5) |
| (5,19) | (12,4) | (19,18) |
如下是計算過程,以及散點圖:
GF(2k) 上的橢圓曲線
最後:
考慮方程 Q = kP,其中Q, P ∈ Ep(a, b) 且 k < p 。
對於給定的 k 和 P 計算 Q 比較容易,而對給定的 Q 和 P 計算 k 則比較困難。這就是橢圓曲線的離散對數問題。