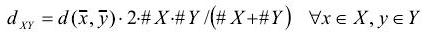備註：本文是閱讀一篇碩士論文《大規模資料聚類技術研究與實現》後的筆記整理，敬請閱讀，並向原作者錢彥江致敬
<一>概念透析
1、什麼是聚類？
基於“物以類聚”的樸素思想，是將物理或抽象物件集合劃分為由類似的物件組成的多個類或簇（cluster）的過程
ps:聚類使得每個簇中的資料點之間最大程度的相似，而不同簇中的資料點之間最大程度的不同
2、聚類分析的數學描述
給定資料集合V={vi|i=1,2,…,n},其中Vi為資料物件，根據資料物件間的相似程度將資料集合分成k組，{Cj|j=1,2,…,k},Cj⊆V,並滿足：
1）Ci ∩ Cj=Φ,i≠j
2）⋃Ci=V
則該過程稱為聚類，Ci,i=1,2,…,k成為簇
3、小結
在機器學習領域聚類與分類不同，它是一種無監督的學習過程。聚類一般沒有訓練過程，它直接處理未知樣本，把這些樣本聚合成不同的簇。
<二>聚類分析中的資料結構和資料型別

1、資料結構（這裡僅介紹兩種具有代表性的資料結構）
(1)資料矩陣(data matrix,也稱物件—變數結構)

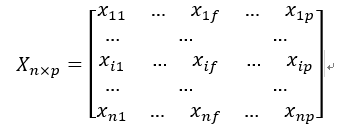
用p個屬性(也稱度量)來表現n個物件
(2)相異度矩陣(dissimilarity matrix,也稱物件—物件結構)
儲存n個物件兩兩之間的相異性（或相似性）， 表現形式是一個n*n維的矩陣

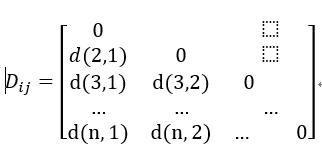
d(i,j)是物件i和物件j之間相異性的量化表示，i和j越相似，d(i,j)就越接近於0，物件越不同，其值越大
2、資料型別
常見：區間標度變數，二元變數，標稱型，序數型，比例標度型變數，混合型別的變數以及向量。
<三>聚類分析中的距離度量（也即相似程度）
在聚類的定義中我們提到了資料點之間的相似程度，那麼這個相似程度可度量的標準是什麼呢？
一般來說，兩個詞：”相似度”,”相異度”
相似度和相異度存在一種互斥的關係，一般可通過下面的公式進行轉換：
d=1-s 或 d=1/s - 1 即 s=1/(d+1)
ps: d相異度 s相似度
相異度和相似度可以統稱為距離，聚類中的距離度量一般分為資料物件間、簇間、資料物件與簇間
1）資料物件間的距離度量
對於p維向量xi和xj，他們之間的距離度量有如下幾種方法
<1>明氏距離（Minkowski Distance）:
d(xi,xj) =
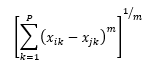
<2>曼哈頓距離（Manhattan Distance）:
當明氏距離的m=1時即為曼哈頓距離，公式為，

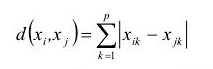
<3>歐式距離（Euclidean Distance）:
當明氏距離的m=2時即為歐氏距離，公式為

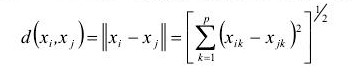
<4>馬氏距離（Mahalanobis Distance）:
基於屬性間的協方差矩陣給予每維不同的權值來定義距離

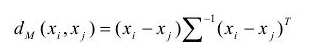
<5>餘弦距離（Cosine Distance）：常用於向量之間的相似度計算

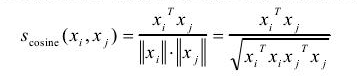
當兩個向量方向相近時，夾角餘弦值較大，反而則較小
特殊的，當兩個向量平行時，夾角餘弦值為1；而當正交時，餘弦值為0
因為夾角餘弦函式忽略了各個向量的絕對長度，著重從形狀方面考慮他們之間的關係，因而我們在使用夾角餘弦前，一般需要先將向量進行歸一化處理

前四種是基於測度的距離定義，需滿足一下四個條件：
(1)D(xi,xj)>=0,距離非負
(2)D(xi,xi) = 0 ,物件與自身的距離為0
(3)D(xi,xj) = D(xj,xi) 對稱性
(4)D(xi,xj) <= D(xi,xk) + D(xk,xj) 三角不等式

2)資料簇間的距離度量（應用在層次聚類方法中）
常見方法如下：
最小距離（Single Linkage）：

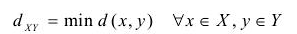
最大距離（Complete Linkage）:

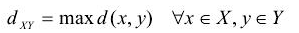
平均距離（Average Linkage 或 UPGMA Distance）:

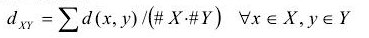
質心法（Centroid Distance）:以兩類各自的樣本均值間的距離作為簇間距離

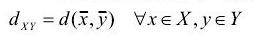
離差平方和法（Ward Distance）:

3）資料物件與資料簇之間的距離度量
可以把資料物件看作只含有一個數據物件的簇，使用簇與簇之間的距離度量方法即可

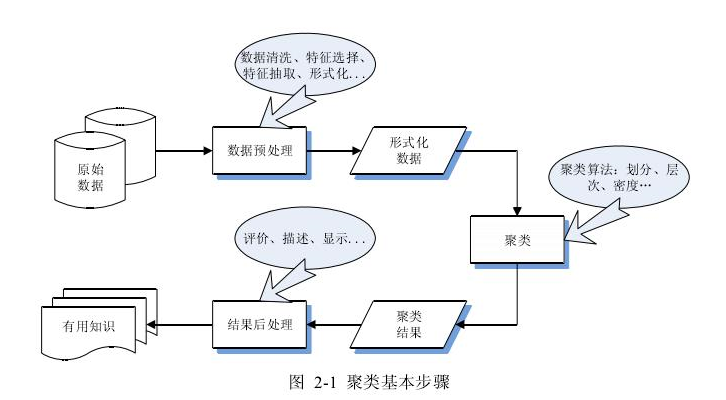
<四>聚類基本步驟