視覺slam-----第二篇 相機和影象
阿新 • • 發佈:2019-01-08
視覺slam系列更多偏向對本人的記錄而非講解,因此敘述部分會佔多數,推導過程幾乎沒有,文章主要內容摘自《視覺slam十四講》《計算機視覺中的多檢視幾何》《機器人學中的狀態估計》,部落格內容僅為幫助自己記憶,本人僅起到總結作用,所有內容均摘自以上幾本書。
相機模型
畫素座標系
針孔相機模型
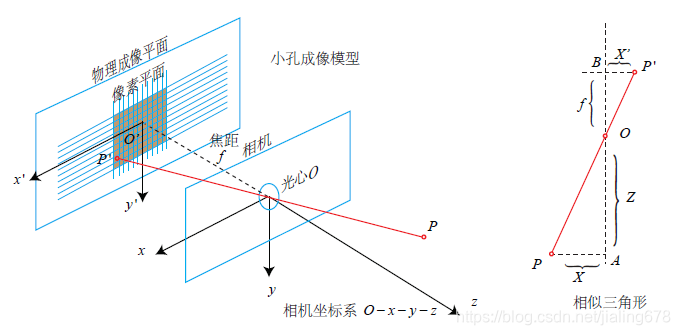
代表相機的焦距,空間上有某點P
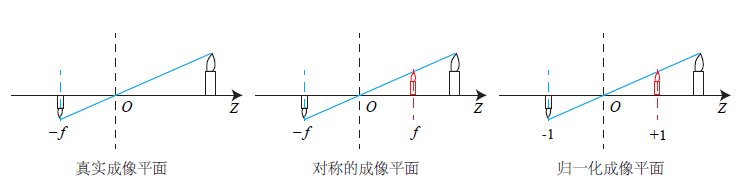
真實成像平面,對稱成像平面,歸一化成像平面的圖示(上圖)。整理得:
畫素座標系通常的定義方式是:原點 位於影象的左上角, 軸向右與x 軸平行, 軸向下與y 軸平行。畫素座標系與成像平面之間,相差了一個縮放和一個原點的平移。我們設畫素座標在 軸上縮放了 倍,在 上縮放了 倍。同時,原點平移了 。那麼,P′ 的座標與畫素座標 的關係為:
整理後得:
其中, 的單位為米, 的單位為畫素每米,所以 的單位為畫素。把該式寫成矩陣形式,會更加簡潔,左側需要用到齊次座標:
把Z 挪到左側:
