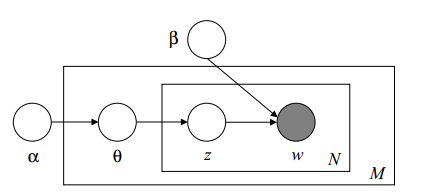
LDA變分法和取樣法
阿新 • • 發佈:2019-01-08
目前比較方便的LDA解法是gibbs取樣,但是對於改進型LDA,如果分佈不再是dirchlet分佈,p(z|w)可能就不太好求了(這裡z代表隱藏變數,w是觀察量),只能用變分法。
LDA變分EM演算法
LDA主要完成兩個任務,給定現有文件集合D,要確定超引數
這裡採用模型是比較原始的LDA模型,論文參考blei的2003年論文和“Note 1: Varitional Methods for Latent Dirichlet Allocation”
(這裡
首先我們想計算出
可以參見prml書的第九章和第十章,採用EM演算法。
由於KL>=0,所以L顯然是ln(p(D∣α,β))的一個下界。首先讓下界最大,即如果模型引數固定,那麼左式顯然是一個固定的常數,當且僅當KL最小的時候,即q(θ,z)是引數的後驗概率時成立。
這裡假定q的形式是已知的,變分引數未知,也就是假定:
上面的這一過程就是E步,即在給定模型引數的情況下試圖使下界儘可能大的一個過程,所表現出來的形式就是L函式可以是一個函式關於隱含變數後驗期望的表示。
下面介紹M步。即對於前面變分引數確定後,q(\theta,z|\gamma,\phi)已知了,L函式也表示出來了,那麼接下來就是使得L函式關於
(Note:在E步時,因為推斷的是文件相關的變分引數和隱藏變數,而文件之間相互獨立,所以可以用一篇文件w代替文件集D;而M步的模型引數是針對全文件集的,因此必須使用D)
LDA的gibbs取樣
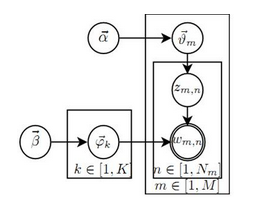
詳細過程參考LDA數學八卦。這裡主要做一些補充解釋。
以該書推導過程為例,首先gibbs取樣前提是假設超引數已知,然後任務是推斷隱藏變數分佈或者說隱藏變數的期望。也就是實際上估計:
(NOTE:估計引數指得到一個固定的具體的值;估計隨機量首先必須要得到該分佈,或以概率最大的點MAP代替該隨機量;或採樣後以期望代替該隨機量)