ASL（Average Search Length），即平均查詢長度，在查詢運算中，由於所費時間在關鍵字的比較上，所以把平均需要和待查詢值比較的關鍵字次數成為平均查詢長度。

它的定義是這樣的：

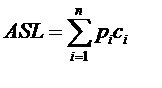
其中n為查詢表中元素個數，Pi為查詢第i個元素的概率，通常假設每個元素查詢概率相同，Pi=1/n，Ci是找到第i個元素的比較次數。

當然，有查詢成功，就有查詢不成功，即要查詢元素不在查詢表中。針對不同查詢方式的查詢成功與不成功，我接下來會說，這也是一我一開始有點亂的地方。

一個演算法的ASL越大，說明時間效能差，反之，時間效能好，這也是顯而易見的。

• 在順序查詢(Sequence Search)表中，查詢方式為從頭掃到尾，找到待查詢元素即查詢成功，若到尾部沒有找到，說明查詢失敗。。所以說，Ci（第i個元素的比較次數）在於這個元素在查詢表中的位置，如第0號元素就需要比較一次，第一號元素比較2次......第n號元素要比較n+1次。所以Ci=i；所以 

            可以看出，順序查詢方法查詢成功的平均 比較次數約為表長的一半。當待查詢元素不在查詢表中時，也就是掃描整個表都沒有找到，即比較了n次，查詢失敗

• 折半查詢(Binary Search)，首先待查詢表是有序表，這是折半查詢的要求。在折半查詢中，用二叉樹描述查詢過程，查詢區間中間位置作為根，左子表為左子樹，右子表為右子樹，，因為這顆樹也被成為判定樹(decision tree)或比較樹(Comparison tree)
  。查詢方式為(找k)，先與樹根結點進行比較，若k小於根，則轉向左子樹繼續比較，若k大於根，則轉向右子樹，遞迴進行上述過程，直到查詢成功或查詢失敗。在n個元素的折半查詢判定樹中，由於關鍵字序列是用樹構建的，所以查詢路徑實際為樹中從根節點到被查結點的一條路徑，因為比較次數剛好為該元素在樹中的層數。所以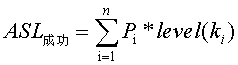Pi為查詢k的概率，level(Ki)為k對應內部結點的層次。而在這樣的判定樹中，會有n+!種查詢失敗的情況，因為將判定樹構建為完全二叉樹，又有n+1個外部結點(用Ei(0<=i<=n)表示)，查詢失敗，即為從根結點到某個外部結點也沒有找到，比較次數為該內部結點的結點數個數之和，所以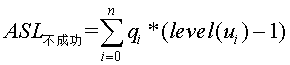，qi表示查詢屬於Ei中關鍵字的概率，level(Ui)表示Ei對應外部結點的層次。所以，在一顆有n個結點判定樹中，總數，所以判定樹高度為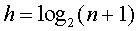的滿二叉樹,第i層上結點個數為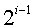，查詢該層上的結點需要進行i次比較，因此，在等概率情況下ASL為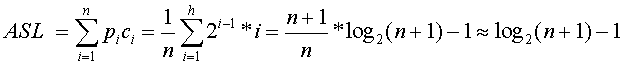                                         
• 例：給11個數據元素有序表（2,3,10,15,20,25,28,29,30,35,40）採用折半查詢。則ASL成功和不成功分別是多少？首先畫出判定樹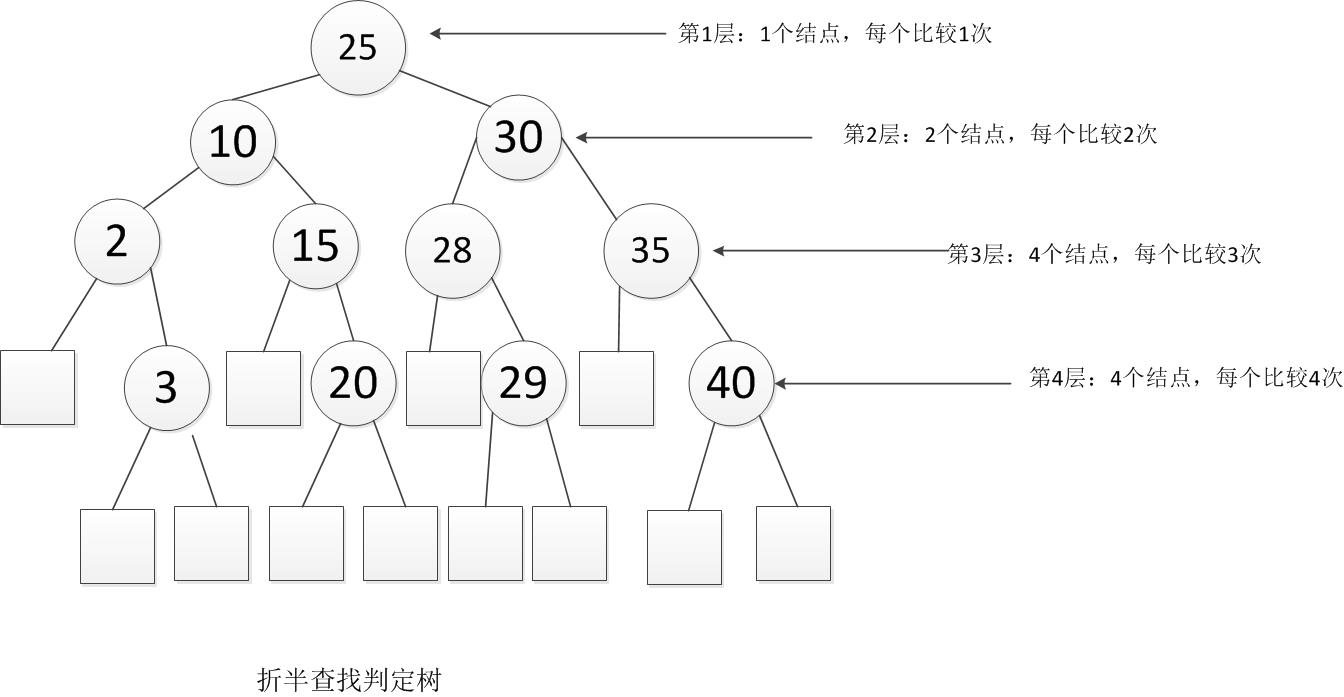，     查詢成功時總會找到途中某個內部結點，所以成功時的平均查詢長度為 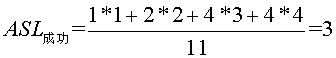即25查詢一次，成功，10,30要查詢2次，成功，2,15,28,35要查詢3次，成功，3,20,29,40要查詢4次，成功。 而不成功的平均查詢長度為  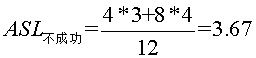，為什麼這麼算呢，因為內部結點都能查詢成功，而查詢不成功的就是那些空的外部結點，所以到查詢到2的左孩子，15的左孩子，28的左孩子，35的左孩子，3的左右孩子，20的左右孩子，29的左右孩子，40的左右孩子時，都是查詢不成功的時候。如我要找1，比25小，裝向左子樹，比較一次，比10小，轉左子樹，2次，比2 小，轉左子樹，3次，此時2五左子樹，所以失敗。所以 。

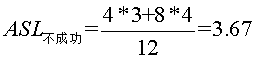•  雜湊表中的ASL   查詢成功的平均查詢長度是指查詢到雜湊表中已有關鍵字的平均探測次數。而查詢不成功的平均查詢長度是指在雜湊表中找不到待查的元素，最後找到空位置元素的探測次數平均值。

• 例：散列表長度為13，地址空間為0~12，雜湊函式H(k) =K mod 13,對關鍵字序列{19,14,23,01,68,20,84,27,55,11,10,79}  所以線性探測結果為：

   

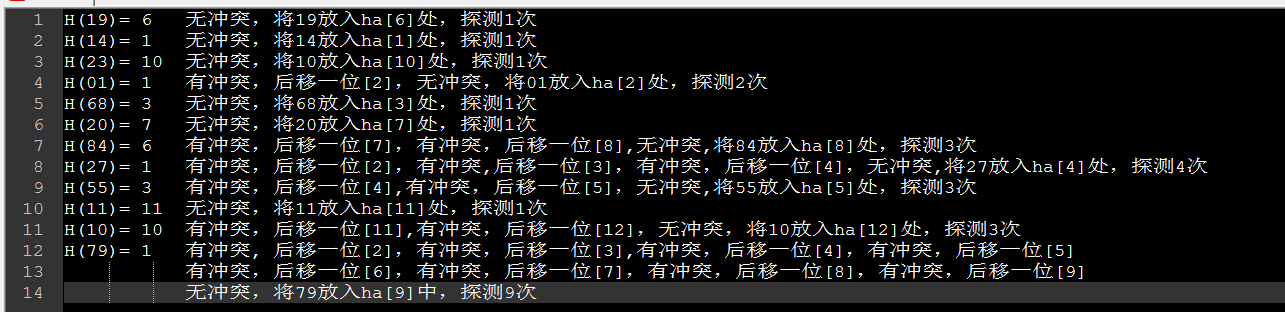
根據探測次數，

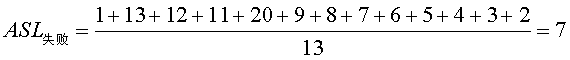          當然成功的很好理解，12個元素，每個元素的探測次數之和除以12就行。而不成功的計算是這樣的。散列表長度為13，根據定義，假設待查關鍵字不在散列表中，要一直找到空元素才算查詢失敗，如H[0]為空，與待查詢元素不等，不成功，比較一次，H[1]，此時H[1]的元素與原本放在H[1]的元素不等(假設不散列表在之中，但也不是空的)，繼續向後比，與H[2]比也不等，繼續向後，一直到H[12]，也不等，繼續向後時，回到H[0]，為空，也不等，查詢失敗，總計比較13次，然後計算第二號元素，，一樣的比較，一直把每個位置都統計一遍，從而得出ASL不成功的.

• 以上就是對ASL的小小總結，為了加強自己的理解，也便於自己以後的回顧和修改，還有有一點很開心的是，最為新蘭黨，總算讓我在2019年初等到了洗衣機和蘭醬的休學旅行，很滿意了。