《程式設計之法》1.4字串轉換成整數
題目描述:輸入一個由數字組成的字串,請把它轉換成整數輸出
分析:int型整數的範圍為:-2147483648~+2147483647,這意味著字串輸入太長會沒辦法正常顯示數字,故當轉換後的數大於最大正數時,我們顯示2147483647;當轉換後的數小於最小負數時,我們顯示-2147483648。
同時需要考慮字串中含有非數字字元,以及字串前有空格等情況,如" 123t444",這時我們規定輸出123。此外,還應該考慮到字串中含有正負號的問題。這些都是小問題,主要需要考慮溢位的情況:
如下,先寫一個小程式分析unsigned與int的轉換關係:
#include <iostream> using namespace std; int main(){ cout << "-1 = " << -1 << ", unsigned(-1) = " << unsigned(-1) << ", (int)((unsigned)(-1)) = " << (int)((unsigned)(-1)) << endl; cout << "-(unsigned)1 = " << -(unsigned)1 << " 或 " << (unsigned)(-(unsigned)1) << endl;//輸出 4294967295 或 4294967295 unsigned tmp = -(unsigned)1; int nums[32], cnt = 0; do{ nums[cnt] = tmp % 2; tmp /= 2; ++cnt; }while(cnt < 32); cout << "-(unsigned)1的unsigned值為: "; for(cnt = 31; cnt >= 0; --cnt) cout << nums[cnt];//輸出11111111111111111111111111111111 cout << endl << "-(unsigned)1的int值為: " << (int)tmp << endl;//輸出-1 cout << "(unsigned)~0 >> 1 = " << ((unsigned)~0 >> 1) << endl; //輸出2147483647 cout << "(int)(unsigned)~0 >> 1 = " << (int)((unsigned)~0 >> 1) << endl;//輸出2147483647 cout << "-((unsigned)~0 >> 1) = " << -((unsigned)~0 >> 1) << endl;//輸出2147483649 cout << "-(int)((unsigned)~0 >> 1) = " << -(int)((unsigned)~0 >> 1) << endl;//輸出-2147483647 int MAX_INT = (int)((unsigned)~0 >> 1); int MIN_INT = -(int)((unsigned)~0 >> 1) - 1; }
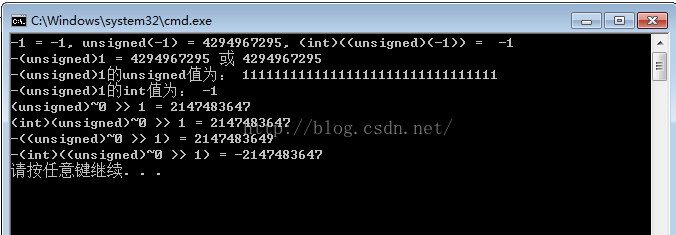
分析:
第一句:由第一條語句的輸出也表明對於程式碼中的常量,編譯器預設它為int型,即有符號型,當加上unsigned做變換後,此後該常量變為無符號型,並按照它所儲存的補碼形式計算輸出,若將其再加上int強制變換,則它此後便又是int型。
第二句到第十三句做了驗證和int,unsigned轉換分析:對1而言,(unsigned)1的在計算機中的補碼儲存形式為:00000000000000000000000000000001。對於-(unsigned)1, 加上負號後,就是大學裡學過的知識(我記憶的口訣是:若為負數的二,十進位制轉換,按照"二對加;對十減"):令最高位的符號位變為1,其他位不變,即為它的原碼;各位取反(符號位除外),即變為它的反碼;最後將反碼加1,即變為補碼,故最後-(unsigned)1在計算機的補碼儲存形式為:11111111111111111111111111111111。
-(unsigned)1的值應該是將-(unsigned)1的補碼儲存形式按照無符號常量的補碼儲存形式來看,故大小為2^31 + 2^30 + ... + 2^0 = 4294967295。根據第一句分析,(unsigned)(-(unsigned)1) = -(unsigned)1。而(int)(-(unsigned)1)是將它的補碼儲存形式按照int來看,即需“對十減”,先將11111111111111111111111111111111反過來,為全0,再變為十進位制為0,再減1,即(unsigned)(-(unsigned)1)=-1。
因此,我們若想求int的最大正數,而int的最大正數的補碼形式為01111111111111111111111111111111,而((unsigned)~0 >> 1)對應的無符號型補碼儲存形式正好與int型的補碼儲存形式一致。故可直接int強制轉換。
若想求int的最小負數,由於(int)((unsigned)~0 >> 1)已經是int型別,故可直接加負號變為-2147483647,再減去1就為int型別中最小的負數,至於補碼的變換就不細述了。
-((unsigned)~0 >> 1):之所以輸出2147483649,是因為加上負號後,其補碼儲存形式01111111111111111111111111111111變為10000000000000000000000000000001,而它又為無符號型,故輸出2147483649。
總結:對於程式中使用的常量,編譯器預設該常量為int型,當對其使用過unsigned後,該常量就變為unsigned型,此後也可對其再次強制轉換為int型。對一個常量取int或unsigned值時,要根據該常量在計算機中的補碼儲存形式,按照int和unsigned的各自規則得出正確求值。當int轉unsigned型時,若int為正或0,則兩者補碼儲存形式一致,大小不會變;若int為負,此時根據int型的補碼儲存形式按照無符號的求值方式來計算無符號數的大小,大小肯定會改變;當unsigned轉int時,若unsigned的二進位制最高位為0,很顯然,大小不會改變;若unsigned的二進位制最高位為1,按照int負數的二進位制轉十進位制的方法求int值,大小肯定也會改變;當對int值加負號時,int值變為其相反數;當對unsigned加負號時,其補碼儲存形式最高位置1,之後除最高位外按位取反,最後減1,獲得其最終補碼形式。
如下,先考慮以下有問題的程式片段:
while(isdigit(*str)){
int c = *str - '0';
if(sign == '+' && (c > (MAX_INT-n*10))){
n = MAX_INT;
break;
}
else if(sign == '-' && (c - 1 < (MAX_INT-n*10)){
n = MIN_INT;
break;
}
n = n*10 + c;
++str;
}解決方式有兩種,a,
既然得到一個負數,就強制轉換為int型,即條件語句變為if(sign == '+' && (c > (int)(MAX_INT-n*10))),這樣最後相減為負數也能判斷出來,並且相減得到的正數的二進位制補碼最高位也不可能為1;
b,之所以有上述問題的存在,主要原因在於有減法的存在,故將條件語句改為if(sign == '+' && (n == MAX_INT/10 && c > MAX_INT%10) || (n > MAX_INT/10),這樣就能考慮到溢位的問題,前者可應對8900000000,1052254545等這種情況,後者可應對2147483649這種情況。
當然n為負數時下面的程式碼也需要相應的改變,下面是程式碼:
#include <iostream>
#include <string>
using namespace std;
int StrToInt(string &str){
int MAX_INT = (int)((unsigned)~0 >> 1);
int MIN_INT = -(int)((unsigned)~0 >> 1) - 1;
if(str.size() == 0) return 0;
//去掉空格
int i = 0;
while(str[i] == ' ') ++i;//測試過string會自動過濾字串前面的空格
//處理正負
int sign = 1;
if(str[i] == '-' || str[i] == '+'){
if(str[i] == '-')
sign = -1;
++i;
}
//確定是數字後進行迴圈
unsigned n = 0;
while(i < str.size() && isdigit(str[i])){
int c = str[i] - '0';
/**********************處理溢位***********************/
if(sign > 0 && ((n > (unsigned)MAX_INT/10) || (n == (unsigned)MAX_INT/10 && c > (unsigned)MAX_INT%10))){
n = (unsigned)MAX_INT;
break;
}
if(sign < 0 && ((n > (unsigned)MIN_INT/10) || (n == (unsigned)MIN_INT/10 && c > (unsigned)MIN_INT%10))){//書中為(unsigned)(MIN_INT/10)),這是因為MIN_INT的補碼為100...00,unsigned強制轉換後,也正好為2147483648
n = (unsigned)MIN_INT;
break;
}
/**********************處理溢位***********************/
//把之前得到的數字乘以10,再加上當前字元表示的數字
n = n*10 + c;
++i;
}
//前面是對無符號進行分析,最後將無符號轉換為int輸出
if(sign < 0 && n != (unsigned)MIN_INT)
return -(int)n;
else
return (int)n;
}
int main(){
string str;
while(cin >> str)
cout << StrToInt(str) << endl;
return 0;
}解法二:
如下,我僅修改了/***/ ~ /***/間的程式碼,思路是因為無符號範圍大,故以無符號數相減,小無符號減大無符號數必定會使二進位制最高位變為1,即轉成int後變為負數:
#include <iostream>
#include <string>
using namespace std;
int StrToInt(string &str){
int MAX_INT = (int)((unsigned)~0 >> 1);
int MIN_INT = -(int)((unsigned)~0 >> 1) - 1;
if(str.size() == 0) return 0;
//去掉空格
int i = 0;
while(str[i] == ' ') ++i;
//處理正負
int sign = 1;
if(str[i] == '-' || str[i] == '+'){
if(str[i] == '-')
sign = -1;
++i;
}
//確定是數字後進行迴圈
unsigned n = 0;
while(i < str.size() && isdigit(str[i])){
int c = str[i] - '0';
/**********************處理溢位***********************/
if(sign > 0 && (c > (int)(MAX_INT - n*10))){
n = (unsigned)MAX_INT;
break;
}
if(sign < 0 && ((c > (int)((unsigned)MIN_INT - n*10)))){
n = (unsigned)MIN_INT;
break;
}
/**********************處理溢位***********************/
//把之前得到的數字乘以10,再加上當前字元表示的數字
n = n*10 + c;
++i;
}
//考慮無符號向int資料的轉換
if(sign < 0 && n != (unsigned)MIN_INT)
return -(int)n;
else
return (int)n;
}
int main(){
string str;
while(cin >> str)
cout << StrToInt(str) << endl;
return 0;
}