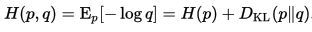相關參考資料見正文

Good-turing模型：

由於我們是估算對於一個位置上出現單詞wi的概率。這種情況下，在樣本庫中沒有出現的單詞，其概率並非為0. 但由於已有的Nr`r的累計和已經達到了1，所以必須採用一個“騰挪“的辦法，將一部分的概率分佈騰挪給未出現的單詞。

解決辦法就是在計算累計出現次數較少的單詞時，將其概率替換為一個較小的值（此處的辦法是將r替換為r‘）

r^* = (r+1)*{n_{r+1}/n_r}

也就是說：這個變化預設認為：n_{r+1}/n_r這一下降速率顯著的大於r+1/r的增長速率 

（因為在r-Nr符合Zipf定律）

http://www.52nlp.cn/mit-nlp-third-lesson-probabilistic-language-modeling-fifth-part

https://en.wikipedia.org/wiki/Zipf%27s_law

條件熵/互資訊/相對熵/交叉熵：

都是基於引入特定字元可以獲得多少資訊量這樣一個概念進行的定義

條件熵：H(X|Y) 

從資訊理論的角度消除不確定性： 與H(X)相比，引入Y後可以消除一定的不確定性。具體的不確定性即為條件熵（特定條件下的熵）

互資訊：I(X,Y)=H(X)=H(X|Y) 關心不確定性的減少程度

所以，引入確定性(新 的制約條件Y)，則可以降低（或至少持平）整個系統的熵

相對熵/交叉熵：兩個分佈的差異性

------條件熵是兩個變數的差異性而 相對熵是兩個分佈的差異性。

相對熵公式：

與前面的兩個概念相比，相對熵/交叉熵關注的是一個數據的一組分佈（一個足夠大的資料量下的分佈形態）下的熵

即某個資料的兩種分佈下，其熵的差值。

用資訊理論的方法表述：對指定的一組資料，用P(i)和Q(i)來擬合相應的資料的資訊量。以P作為基準，衡量Q相對於P，表達這一組資料所需的資訊量的差值。

如果P是理想最佳分佈（例如嚴格按單詞出現次數求和統計的p`log(p)）,Q是我們自己設計的一組分佈情況。則評價Q的均衡性的辦法，就是用Q(i)的資訊長度去乘以P(i)，最後累加得到對理想P分佈而言，Q分佈的熵的差值（也就是和P相比有多大的差異性）

交叉熵公式是相對熵+E(p)：可認為是基於Q編碼的總資訊含量

https://www.zhihu.com/question/41252833

稀疏矩陣的快速計算方法

http://www-users.cs.umn.edu/~saad/IterMethBook_2ndEd.pdf

TF-IDF：

TFIDF是：給定詞彙，找出使這個詞彙所能代表的資訊量最大的文件。

可以理解為：

100篇文章均勻的分佈了某單詞（TF），與10篇文章均勻分佈某單詞的熵的差值（IDF修正）。

這個概念是基於相對熵提出的。

即我先假定一個基礎分佈（完全平均P分佈），此時某單詞w的資訊含量就是TF(w)log(TF(w))

而此時我發現其實w符合Q分佈（對於100篇文章中，只有10篇才有這個單詞），那麼增加了這個額外的資訊後，資訊熵就增加了

---------即：單詞w的出現代表了更多的資訊。

因此，乘以IDF引數：log(D/j) 即為log p/log q，修正後的引數才是單詞w的真正資訊量。

最後對搜尋者提供的所有單詞組合，對候選的所有文章進行檢索。按文章中針對提供的單詞組合給出的資訊量最大的網頁進行排列。