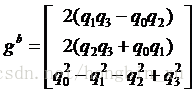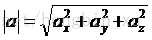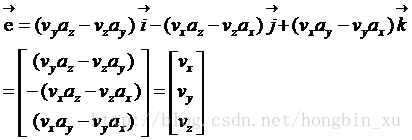上次我們討論了姿態解算基礎理論以及幾個比較重要的公式的一些推導，如果有不熟悉的請點選這裡開啟連結。這次來介紹一些實際的姿態解算演算法吧！
一般在程式中，姿態解算的方式有兩種：一種是尤拉角法，一種是四元數法。這裡不介紹尤拉角法，只介紹四元數法，如有興趣可以去查詢相關資料。

互補濾波演算法：
顧名思義，是多組資料結合互補，並進行濾波處理穩定輸出，得到姿態的演算法。而我們使用的感測器就是加速度計和陀螺儀。加速度計用於測量加速度，陀螺儀用於測量角速度。 加速度計的靜態穩定性更好，而在運動時其資料相對不可靠；陀螺儀的動態穩定性更好，但是靜止時資料相對不可靠。所以，我們可以通過加速度計的輸出來修正陀螺儀的漂移誤差，換句話說，通過加速度計來修正陀螺儀

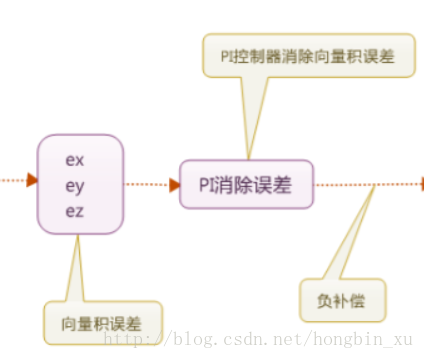
這個是我在網上找到的說明互補濾波法的框圖：（原圖下載：點選這裡開啟)

首先，我們取定導航座標系n中標準重力加速度g，定義為，那麼將導航座標系n下的 轉換為載體座標系b下的：。
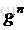
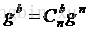
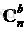
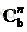
這裡用到了，前面在推導基礎公式時匯出了使用四元數表示的旋轉矩陣。
公式如下：

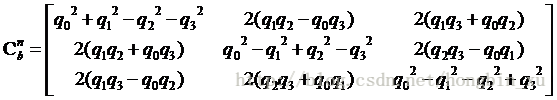
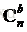
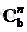
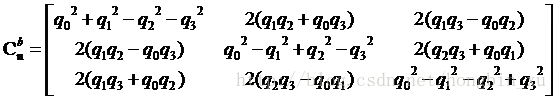
但是我們要用的是，所以還要對 做一個矩陣逆變換。由於它是正交矩陣，對於正交矩陣有這個性質：正交矩陣的逆矩陣等於其的轉置。所以我們很容易得到：

將上式代入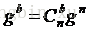 ，而且我們已知，所以得到：

接著再定義載體座標系b中加速度計輸出為a，由於前面計算導航座標系時我們採用的重力加速度是標準重力加速度，所以還需要對其進行歸一化，才能繼續運算。
設加速度計三個軸的值分別是ax，ay，az。
首先求模：

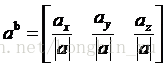
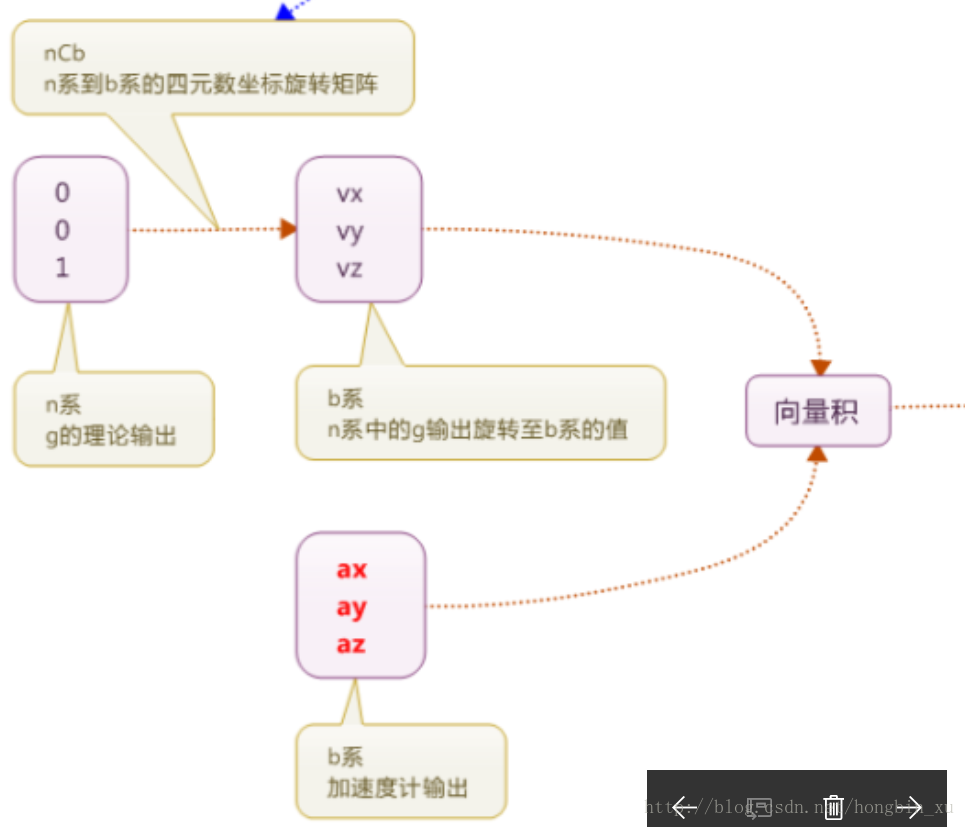
根據框圖的說明再整理一下前面得到的結果：
標準重力加速度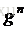從n系轉到b系中的矩陣表示：

b系下加速度計測量得到的加速度的矩陣表示：
（備註：這是歸一化之後的值）

對 和 做向量叉乘，即可得到給陀螺儀的校正補償值e。

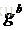
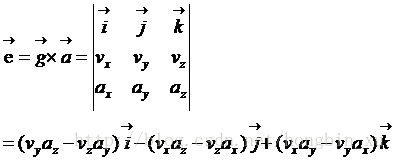
表示成矩陣形式更為直觀：

然後再使用PI控制器進行濾波，準確地說事消除漂移誤差，只要存在誤差控制器便會持續作用，直至誤差為0。控制的效果取決於P和I引數，分別對應比例控制和積分控制的引數。

這裡給出PI控制的公式：

是我們要負反饋給陀螺儀進行校正補償的值， 是比例控制項， 是積分控制項，在程式中採用離散累加計算。關於PID控制理論的東西，這裡不做贅述。

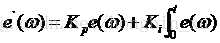
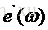
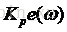
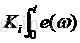
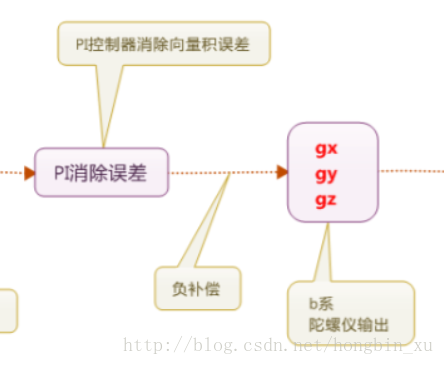
如框圖中所寫，接下來將前面得到的補償值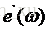加在陀螺儀輸出的資料上進行校正。

跟著框圖往下走：

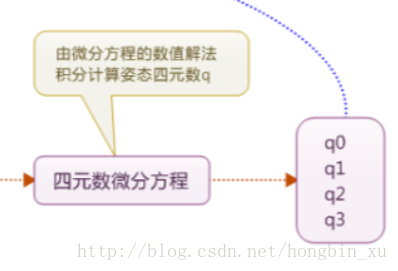
將前面的陀螺儀資料通過四元數微分方程轉換為四元數輸出。
因為有幾個地方我也沒搞懂，所以就簡單介紹一下四元數微分方程，詳細步驟請查閱秦永元的慣性導航一書（第三篇 9.2.3節）：
由於載體的運動，四元數Q是變數，其引數可以表示成關於時間的函式。
使用四元數的三角形式：
為剛體瞬時繞軸轉過的角度， 為歸一化後的位置向量。
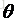
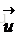
設角速度為：
對四元數的三角表示形式求導：

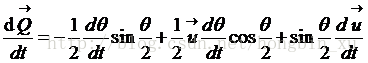
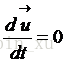
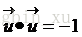
因為 ， 且
所以：

將上式表示成矩陣形式：

或者
上面的兩個公式被稱為四元數微分方程。利用陀螺儀的資料進行離散累積便可得到四元數的值，最後再轉換成尤拉角形式輸出即可。

再附上程式碼：

////////////////////////////////////////////////////////////////////////////////
#define Kp 10.0f                        // proportional gain governs rate of convergence to accelerometer/magnetometer
#define Ki 0.008f                          // integral gain governs rate of convergence of gyroscope biases
#define halfT 0.001f                   // half the sample period取樣週期的一半

float q0 = 1, q1 = 0, q2 = 0, q3 = 0;    // quaternion elements representing the estimated orientation
float exInt = 0, eyInt = 0, ezInt = 0;    // scaled integral error
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az)
{
  float norm;
//  float hx, hy, hz, bx, bz;
  float vx, vy, vz;// wx, wy, wz;
  float ex, ey, ez;

  // 先把這些用得到的值算好
  float q0q0 = q0*q0;
  float q0q1 = q0*q1;
  float q0q2 = q0*q2;
//  float q0q3 = q0*q3;
  float q1q1 = q1*q1;
//  float q1q2 = q1*q2;
  float q1q3 = q1*q3;
  float q2q2 = q2*q2;
  float q2q3 = q2*q3;
  float q3q3 = q3*q3;

    if(ax*ay*az==0)
        return;

  norm = sqrt(ax*ax + ay*ay + az*az);       //acc資料歸一化
  ax = ax /norm;
  ay = ay / norm;
  az = az / norm;

  // estimated direction of gravity and flux (v and w)              估計重力方向和流量/變遷
  vx = 2*(q1q3 - q0q2);                                             //四元素中xyz的表示
  vy = 2*(q0q1 + q2q3);
  vz = q0q0 - q1q1 - q2q2 + q3q3 ;

  // error is sum of cross product between reference direction of fields and direction measured by sensors
  ex = (ay*vz - az*vy) ;                                             //向量外積在相減得到差分就是誤差
  ey = (az*vx - ax*vz) ;
  ez = (ax*vy - ay*vx) ;

  exInt = exInt + ex * Ki;                                //對誤差進行積分
  eyInt = eyInt + ey * Ki;
  ezInt = ezInt + ez * Ki;

  // adjusted gyroscope measurements
  gx = gx + Kp*ex + exInt;                                              //將誤差PI後補償到陀螺儀，即補償零點漂移
  gy = gy + Kp*ey + eyInt;
  gz = gz + Kp*ez + ezInt;                                          //這裡的gz由於沒有觀測者進行矯正會產生漂移，表現出來的就是積分自增或自減

  // integrate quaternion rate and normalise                           //四元素的微分方程
  q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
  q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
  q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
  q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;

  // normalise quaternion
  norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
  q0 = q0 / norm;
  q1 = q1 / norm;
  q2 = q2 / norm;
  q3 = q3 / norm;

  //Q_ANGLE.Yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3; // yaw
  Q_ANGLE.Y  = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch
  Q_ANGLE.X = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll
}

這段程式碼網上很多地方都可以看見，匿名四軸（老版本的）的程式也是用的這段。
上面也添加了一些註釋，把互補濾波演算法的理論部分過了一遍後再來對著程式碼讀一遍，應該不會覺得有多難了吧。程式中就只是把前面推導的公式一個個用上去了而已，如果不懂原理直接使用也不會有太大問題。
程式中的積分運算是採用離散累積的方法運算的。PID控制器只是起到了一個穩定資料消除漂移誤差的作用。

希望這些筆記能給更多的人提供幫助，歡迎交流指正。