【資料結構】棧及棧的應用
棧
棧是一種先進後出的的特殊線性表,只允許在固定的一端進行插入和刪除元素操作,進行輸入插入和刪除操作的一端稱為棧頂,另一端稱為棧底
下面採用靜態順序表實現的方式簡單封裝一個棧
儲存方式
#define MAX_SIZE 100
typedef int DataType;
typedef struct
{
DataType arr[MAX_SIZE];
int top;
}Stack;
相應操作
void StackInit(Stack *ps)
{
ps->top = 0;
}
void StackDestroy(Stack *ps)
{
ps->top = 0;
}
void 棧的應用
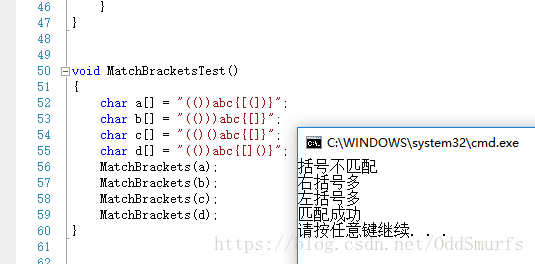
括號匹配問題
將需要檢驗的文件以字串的方式表示,遍歷整個字串,遍歷的過程中會出現三種情況
(1)左括號:遇到左括號進行入棧操作
(2)右括號:遇到右括號需要判斷棧當前的狀態。如果棧為空,則直接可以斷定右括號多(在遍歷的過程中只有左括號入棧);如果棧不為空,則判斷棧頂元素和當前遍歷到的括號是否匹配,如果匹配則出棧,不匹配表明不匹配
(3)其他字元:不做處理,繼續向後遍歷
遍歷完整個字串的時候判斷最後棧是否為空,為空則表示括號匹配,如果不為空,則表示左括號多
void MatchBrackets RPN求值
為了方便用C語言對字尾表示式進行標識,用結構體和列舉進行封裝,用Item型別的陣列來存放整個字尾表示式
typedef enum
{
NUMBER,
OPRETOR
}Type;
typedef enum
{
ADD,
SUB,
MUL,
DIV
}OP;
typedef struct
{
Type type;
int number;
OP opreator;
}Item;
遍歷整個陣列,遇到運算元壓棧
遇到操作符連續出棧兩次,根據此運算元對出棧的兩個運算元做相應處理,然後將結果壓入棧中(要注意DIV 和 SUB操作時,左右兩個運算元的順序)
遍歷完整個陣列,棧中只剩下的最後一個元素,則是整個表示式的結果
int RPN(Item *arr, int sz)
{
Stack stack;
int operand1 = 0;
int operand2 = 0;
OP tmp;
StackInit(&stack);
while (sz--)
{
if (arr->type == NUMBER)
{
StackPush(&stack, arr->number);
}
else
{
tmp = arr->opreator;
operand1 = StackTop(&stack);
StackPop(&stack);
operand2 = StackTop(&stack);
StackPop(&stack);
switch(tmp)
{
case ADD:
{
StackPush(&stack, operand1+operand2);
}
break;
case SUB:
{
StackPush(&stack, operand2-operand1);
}
break;
case MUL:
{
StackPush(&stack, operand2*operand1);
}
break;
case DIV:
{
StackPush(&stack, operand2/operand1);
}
break;
default:
break;
}
}
arr++;
}
return StackTop(&stack);
}
int main()
{
int result = 0;
Item arr[] = {
{NUMBER, 12, DEFAULT},
{NUMBER, 3, DEFAULT},
{NUMBER, 4, DEFAULT},
{OPRETOR, -1, ADD},
{OPRETOR, -1, MUL},
{NUMBER, 6, DEFAULT},
{OPRETOR, -1, SUB},
{NUMBER, 8, DEFAULT},
{NUMBER, 2, DEFAULT},
{OPRETOR, -1, DIV},
{OPRETOR, -1, ADD},
};
int size = sizeof(arr)/sizeof(arr[0]);
result = RPN(arr, size);
printf("%d\n", result);
return 0;
}
迷宮
採用回溯法來找迷宮出口
回溯法:對一個包括有很多個結點,每個結點有若干個搜尋分支的問題,把原問題分解為若干個子問題求解的演算法。當搜尋到某個結點發現無法再繼續搜尋下去時,就讓搜尋過程回溯到該結點的前一個結點,繼續搜尋該結點外的其他尚未搜尋的分支;如果發現該結點無法再繼續搜尋下去,就讓搜尋過程回溯到這個結點的前一個結點繼續這樣的搜尋過程;一直進行下去,直到搜尋到問題的解或者搜尋完了全部可搜尋的分支沒有解存在為止
藉助棧來完成回溯,用一個二維陣列來構造迷宮,可走路線標記為1,牆標記為0,用一個結構體封裝二維陣列元素的座標,所以與普通棧有差異的是用於存放迷宮位置的資料型別也是一個結構體,封裝了這個二維陣列的橫縱座標
typedef struct Coordinates
{
int x;
int y;
}Coordinates;
typedef Coordinates DataType;
typedef struct
{
DataType arr[MAX_SIZE];
int top;
}Stack;
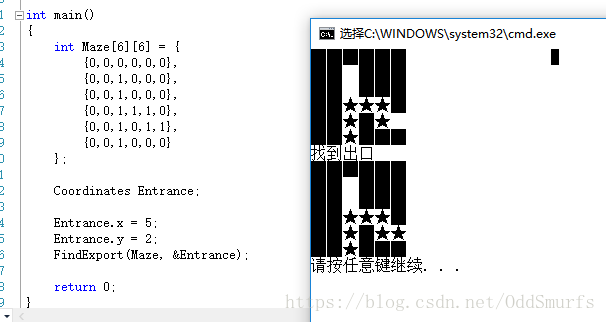
簡單迷宮
二維陣列構造簡單迷宮:
int Maze[6][6] = {
{0,0,0,0,0,0},
{0,0,1,0,0,0},
{0,0,1,0,0,0},
{0,0,1,1,1,0},
{0,0,1,0,1,1},
{0,0,1,0,0,0}
};
按左、上、右、下的順序進行嘗試,將走過的位置壓入棧中,每走一步都對走過的位置進行標記,防止重複迴圈,無路可走時進行回溯,回溯的時候記得出棧,走過的路通過再次標記的方式避免重複走,所以如果能走,則選擇的是與前面不同的路線,在走的過程中判斷當前位置是否為出口,如果是出口函式renturn即可
用棧實現回溯時無法判斷回溯後的位置已嘗試的方向,所以必須要對走之後和回溯過的位置進行標記
void PrintMaze(int Maze[][6])
{
int i = 0;
int j = 0;
for (; i < 6; i++)
{
for (j = 0; j < 6; j++)
{
if (Maze[i][j] == 0)
{
printf("█");
}
else if (Maze[i][j] == 1)
{
printf(" ");
}
else if (Maze[i][j] == 3)
{
printf(" ");
}
else
{
printf("★");
}
}
printf("\n");
}
}
void FindExport(int Maze[][6], Coordinates* p)
{
Stack stack;
Coordinates pos;
StackInit(&stack);
pos.x = p->x;
pos.y = p->y;
StackPush(&stack, pos);//先把入口壓入棧中
while (1)
{
Maze[pos.x][pos.y] = 2;
//左
if (Maze[pos.x][pos.y - 1] == 1)
{
pos.y -= 1;
StackPush(&stack, pos);
Maze[pos.x][pos.y] = 2;
if ((pos.x == 0 || pos.x == 5) || (pos.y == 0 || pos.y == 5))
{
printf("找到出口\n");
PrintMaze(Maze);
return;
}
}
//上
else if (Maze[pos.x - 1][pos.y] == 1)
{
pos.x -= 1;
StackPush(&stack, pos);
Maze[pos.x][pos.y] = 2;
if ((pos.x == 0 || pos.x == 5) || (pos.y == 0 || pos.y == 5))
{
printf("找到出口\n");
PrintMaze(Maze);
return;
}
}
//右
else if (Maze[pos.x][pos.y + 1] == 1)
{
pos.y += 1;
StackPush(&stack, pos);
Maze[pos.x][pos.y] = 2;
if ((pos.x == 0 || pos.x == 5) || (pos.y == 0 || pos.y == 5))
{
printf("找到出口\n");
PrintMaze(Maze);
return;
}
}
//下
else if (Maze[pos.x + 1][pos.y] == 1)
{
pos.x += 1;
StackPush(&stack, pos);
Maze[pos.x][pos.y] = 2;
if ((pos.x == 0 || pos.x == 5) || (pos.y == 0 || pos.y == 5))
{
printf("找到出口\n");
PrintMaze(Maze);
return;
}
}
else
{
Maze[StackTop(&stack).x][StackTop(&stack).y] = 3;
StackPop(&stack);
pos = StackTop(&stack);
}
system("cls");
PrintMaze(Maze);
Sleep(300);
}
}
通路間不帶環
二維陣列構造 通路間不帶環迷宮:
int Maze[7][6] = {
{0,0,0,0,0,0},
{0,1,1,1,1,1},
{0,1,0,0,0,0},
{0,1,0,1,1,1},
{0,1,0,1,0,0},
{0,1,1,1,1,1},
{0,1,0,0,0,0},
};
找到出口將出口堵住,讓其進行回溯再找下一條出口,直到回溯到入口即棧為空時表示找完了所有出口路線
void PrintMaze(int Maze[][6])
{
int i = 0;
int j = 0;
for (; i < 7; i++)
{
for (j = 0; j < 6; j++)
{
if (Maze[i][j] == 0)
{
printf("█");
}
else if (Maze[i][j] == 1)
{
printf(" ");
}
else if (Maze[i][j] == 3)
{
printf(" ");
}
else
{
printf("★");
}
}
printf("\n");
}
}
void FindExport(int Maze[][6], Coordinates* p)
{
Stack stack;
Coordinates pos;
StackInit(&stack);
pos.x = p->x;
pos.y = p->y;
StackPush(&stack, pos);//先把入口壓入棧中
while (1)
{
Maze[pos.x][pos.y] = 2;
//左
if (Maze[pos.x][pos.y - 1] == 1)
{
pos.y -= 1;
StackPush(&stack, pos);
Maze[pos.x][pos.y] = 2;
if ((pos.x == 0 || pos.x ==