最近開始學習C語言的稀疏矩陣的一些知識，現在簡單的整理梳理一下知識脈絡，僅供自己總結學習，歡迎技術指正，拒絕盲噴。

1.首先先介紹一下關於稀疏矩陣的一些基礎知識，關於稀疏矩陣，一直都沒有過很清楚詳細的定義。簡單的說，在M*N的一個矩陣中，假設有t個元素不為0，那麼有計算公式：δ=t/(m*n).稱δ為該矩陣的稀疏因子，一般認為當δ<0.05(並無具體規定)的時候稱該矩陣為稀疏矩陣。

2.一般在操作稀疏矩陣的時候以壓縮儲存為主，稀疏矩陣判定的主要標準是矩陣中非零(Non-Zero)元所佔的比例，所以稀疏矩陣的壓縮基本原理也由此而來，一般需要一個三元組(i,j,Data)來儲存稀疏矩陣中的非零元(直接忽略零元)，三元組(i,j,Data)

例：

M = 

    0  8  0  6  0  2  0

    0  0  34 54 0  0  2

    -7 0  0  0  0  0  0

    0  0  0  0  -12 0 0

M矩陣可由

   （0,1,8）,(0,3,6),(0,6,2),(1,2,34),(1,3,54),(1,6,2),(2,0,-7),(3,4,-12)

的集合唯一表示。

3.下面簡單介紹一下利用稀疏矩陣的壓縮儲存方式進行矩陣的常用運算

轉置運算,是矩陣運算中最簡單的一種，對於一個m*n的矩陣Matrix與它的轉置矩陣Matrix'遵守如下規則：

Matrix(i,j)=Matrix'(j,i);(0≤i＜m，0≤j＜n)

所以我們分析對稀疏矩陣三元組做轉置操作共需要兩個步驟：

    1)將每個三元組中的i和j互換

    2)對三元組重新排序

具體實現程式碼如下：

#include <stdio.h>
#include <string.h>

/**
* @macro definition
*/
#define MAX_NODE_NUM     100
#define MAX_ROW          4
#define MAX_COL          7

/**
* @Global srtuct
*/
typedef struct 
{
    unsigned int ui32Row, ui32Col;
    int si32Data;
}Struct_DataNode;

typedef struct
{
    Struct_DataNode DataNode[MAX_NODE_NUM];
    unsigned int ui32MatrixRow, ui32MatrixCol, ui32DataNodeNum;
}Struct_SparceMatrix;

/**
* @ main function
*/
int main(void)
{
    Struct_SparceMatrix OriginalMatrix, TransMatrix;
    int si32DataNodeNumTemp = 0;

    memset(&OriginalMatrix,0x00,sizeof(OriginalMatrix));
    memset(&TransMatrix, 0x00, sizeof(TransMatrix));

    /**
    * @Original matrix operations
    */
    OriginalMatrix.ui32MatrixRow = MAX_ROW;
    OriginalMatrix.ui32MatrixCol = MAX_COL;

    int si32OriginalMatrixComplete[MAX_ROW][MAX_COL] = 
    {
        {0,8,0,6,0,2,0},
        {0,0,34,54,0,0,2},
        {-7,0,0,0,0,0,0},
        {0,0,0,0,-12,0,0}
    };

    printf("The Original Matrix[%d,%d] is :\n",
        OriginalMatrix.ui32MatrixRow,
        OriginalMatrix.ui32MatrixCol);
    for (unsigned int i = 0; i < OriginalMatrix.ui32MatrixRow; ++i)
    {
        for (unsigned int j = 0; j < OriginalMatrix.ui32MatrixCol; ++j)
        {
            printf("%3d,", si32OriginalMatrixComplete[i][j]);

            if (si32OriginalMatrixComplete[i][j])
            {
                OriginalMatrix.DataNode[OriginalMatrix.ui32DataNodeNum].ui32Row = i;
                OriginalMatrix.DataNode[OriginalMatrix.ui32DataNodeNum].ui32Col = j;
                OriginalMatrix.DataNode[OriginalMatrix.ui32DataNodeNum].si32Data = si32OriginalMatrixComplete[i][j];
                ++OriginalMatrix.ui32DataNodeNum;
            }
        }
        printf("\n");
    }

    printf("Original sparse matrix:\n");
    for (unsigned int i = 0; i < OriginalMatrix.ui32DataNodeNum; ++i)
    {
        printf("[%d,%d,%d]\n",OriginalMatrix.DataNode[i].ui32Row,
                                OriginalMatrix.DataNode[i].ui32Col,
                                OriginalMatrix.DataNode[i].si32Data);
    }

    /**
    * @Transposition matrix operations
    */
    TransMatrix.ui32DataNodeNum = OriginalMatrix.ui32DataNodeNum;
    TransMatrix.ui32MatrixCol = OriginalMatrix.ui32MatrixRow;
    TransMatrix.ui32MatrixRow = OriginalMatrix.ui32MatrixCol;

    printf("Transposition sparse matrix:\n");
    for (unsigned int i = 0,ui32DataNodeNumTemp = 0; i < TransMatrix.ui32MatrixRow; ++i)
    {
        for (unsigned int j = 0; j < TransMatrix.ui32DataNodeNum; ++j)
        {
            if (i == OriginalMatrix.DataNode[j].ui32Col)
            {
                TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Row = OriginalMatrix.DataNode[j].ui32Col;
                TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Col = OriginalMatrix.DataNode[j].ui32Row;
                TransMatrix.DataNode[ui32DataNodeNumTemp].si32Data = OriginalMatrix.DataNode[j].si32Data;
                printf("[%d,%d,%d]\n", TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Row,
                                        TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Col,
                                        TransMatrix.DataNode[ui32DataNodeNumTemp].si32Data);
                ++ui32DataNodeNumTemp;
            }
        }
    }

    printf("The Transposition Matrix[%d,%d] is :\n",
        TransMatrix.ui32MatrixRow,
        TransMatrix.ui32MatrixCol);
    for (unsigned int i = 0, ui32DataNodeNumTemp = 0; i < TransMatrix.ui32MatrixRow; ++i)
    {
        for (unsigned int j = 0; j < TransMatrix.ui32MatrixCol; ++j)
        {
            if (i == TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Row &&
                j == TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Col)
            {
                printf("%3d,",TransMatrix.DataNode[ui32DataNodeNumTemp++].si32Data);
            }
            else
            {
                printf("%3d,", 0);
            }
        }
        printf("\n");
    }    
    return 0;
}
 

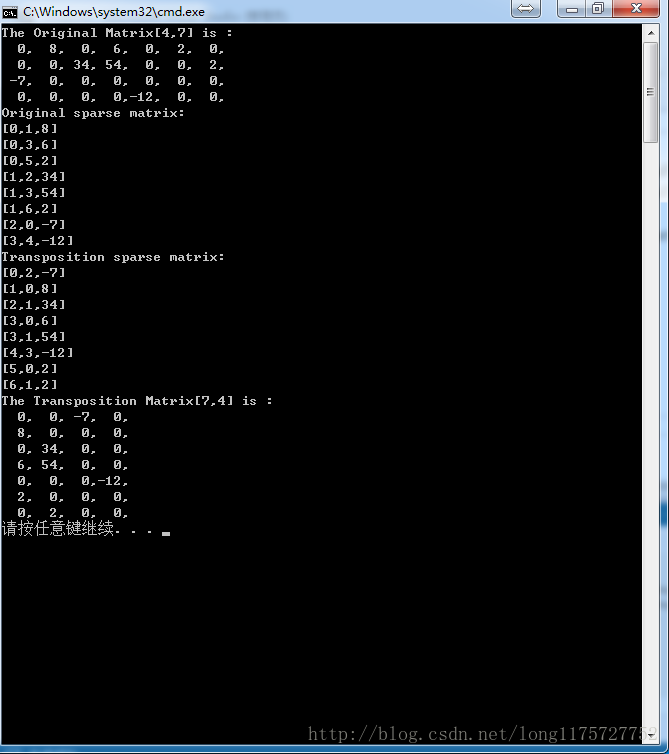
以上程式碼的控制檯輸出如下：

由此可看到，通過稀疏矩陣的三元組表示形式計算矩陣的轉置結果是正確的。

4.最後注意總結的是，在做以三元組做矩陣轉置的時候，程式碼段的時間複雜度是O(TransMatrix.ui32MatrixRow * TransMatrix.ui32DataNodeNum)，可以看出矩陣的行數以及非零元的個數乘積是成正比的，矩陣轉置的經典演算法時間複雜度為O(Row * Col)，當ui32DataNodeNum比較大的時候，時間複雜度比較大。

5.另外，做嵌入式C的同學(尤其微控制器開發或者IC開發)，對程式碼的時間開銷和空間開銷都非常的在意，對於時間開銷的優化需要依據不同場合採用不同的演算法，對於空間開銷，此段程式碼可以採用動態記憶體申請(malloc)的方法進行優化。