優化方法總結

參考

1. SGD

3種不同的梯度下降方法，區別在於每次引數更新時計算的樣本資料量不同。

1.1 Batch gradient descent

每進行1次引數更新，需要計算整個資料樣本集：

θ=θ−η∇θJ(θ)

for i in range(nb_epochs):
    params_grad = evaluate_gradient(loss_function, data, params)
    params = params - learning_rate * params_grad

1.2 Stochastic gradient descent

每進行1次引數更新，只需要計算1個數據樣本：

θ=θ−η∇θJ(x(i),y(i);θ)

for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data:
        params_grad = evaluate_gradient(loss_function, example, params)
        params = params - learning_rate * params_grad

1.3 Mini-batch gradient descent

每進行1次引數更新，需要計算1個mini-batch資料樣本

：

θ=θ−η∇θJ(x(i:i+n),y(i:i+n);θ)

for i in range(nb_epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch_size=50):
        params_grad = evaluate_gradient(loss_function, batch, params)
        params = params - learning_rate * params_grad

【三種gradient descent對比】

Batch gradient descent

的收斂速度太慢，而且會大量多餘的計算(比如計算相似的樣本)。

Stochastic gradient descent雖然大大加速了收斂速度，但是它的梯度下降的波動非常大(high variance)。

Mini-batch gradient descent中和了2者的優缺點，所以SGD演算法通常也預設是Mini-batch gradient descent。

【Mini-batch gradient descent的缺點】

然而Mini-batch gradient descent也不能保證很好地收斂。主要有以下缺點：

選擇一個合適的learning rate是非常困難的

學習率太低會收斂緩慢，學習率過高會使收斂時的波動過大。
所有引數都是用同樣的learning rate

對於稀疏資料或特徵，有時我們希望對於不經常出現的特徵的引數更新快一些，對於常出現的特徵更新慢一些。這個時候SGD就不能滿足要求了。
sgd容易收斂到區域性最優解，並且在某些情況可能被困在鞍點

在合適的初始化和step size的情況下，鞍點的影響沒那麼大。

正是因為SGD這些缺點，才有後續提出的各種演算法。

2. Momentum

momentum利用了物理學中動量的思想，通過積累之前的動量(mt−1)來加速當前的梯度。

mt=μ∗mt−1+η∇θJ(θ)θt=θt−1−mt
其中，μ是動量因子，通常被設定為0.9或近似值。

【特點】

引數下降初期，加上前一次引數更新值；如果前後2次下降方向一致，乘上較大的μ能夠很好的加速。
引數下降中後期，在區域性最小值附近來回震盪時，gradient→0，μ使得更新幅度增大，跳出陷阱。
在梯度方向改變時，momentum能夠降低引數更新速度，從而減少震盪；在梯度方向相同時，momentum可以加速引數更新，從而加速收斂。
總而言之，momentum能夠加速SGD收斂，抑制震盪。

3. Nesterov

Nesterov在梯度更新時做一個矯正，避免前進太快，同時提高靈敏度。

Momentum並沒有直接影響當前的梯度∇θJ(θ)，所以Nesterov的改進就是用上一次的動量(−μ∗mt−1)當前的梯度∇θJ(θ)做了一個矯正。

mt=μ∗mt−1+η∇θJ(θ−μ∗mt−1)θt=θt−1−mt

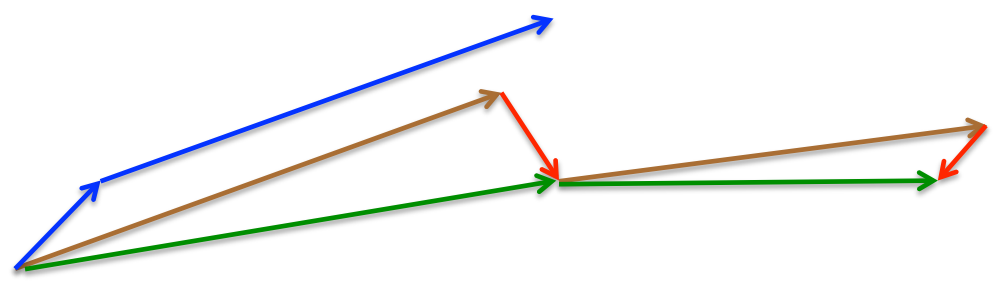
Momentum與Nexterov的對比，如下圖：

Momentum：藍色向量

Momentum首先計算當前的梯度值（短的藍色向量），然後加上之前累計的梯度/動量（長的藍色向量）。
Nexterov：綠色向量

Nexterov首先先計算之前累計的梯度/動量（長的棕色向量），然後加上當前梯度值進行矯正後(−μ∗mt−1)的梯度值（紅色向量），得到的就是最終Nexterov的更新值（綠色向量）。

Momentum和Nexterov都是為了使梯度更新更靈活。但是人工設計的學習率總是有些生硬，下面介紹幾種自適應學習率的方法。

4. Adagrad

Adagrad是對學習率進行了一個約束。

gt=∇θJ(θ)nt=nt−1+(gt)2θt=θt−1−ηnt+ϵ√∗gt=θt−1−η∑tr=1(gr)2+ϵ√∗gt
這個 −1∑tr=1(gr)2+ϵ√ 是一個約束項regularizer，η 是一個全域性學習率，ϵ 是一個常數，用來保證分母非 0。