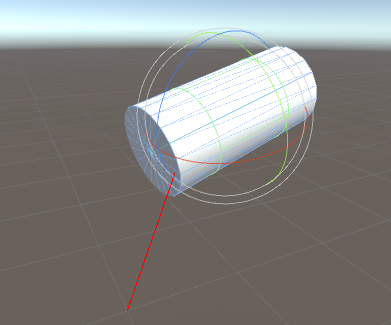
碰撞檢測之Ray-Cylinder檢測
正交基和標準正交基
首先來看定義
Let S = {v1, v2, ... , vk} be a set of vectors in Rn, then S is called an orthogonal if
vi . vj=0
for all i not equal to j. An orthogonal set of vectors is called orthonormal if all vectors in S are unit vectors.
咳咳,翻譯一下
對於 Rn中的一個向量集合 S={v1, v2, ... , vk} , 如果存在
vi . vj = 0 (i != j)
那麼它們就是一組正交基,如果它們都是單位向量,則它們還是標準正交基。
定理
1.給定一組正交基S = {v1, v2, ... , vk},那麼他們是線性相關的。
2.對於 Rn中的一個正交基 S={v1, v2, ... , vk},則 Rn中的向量 v 的以S為基的第 i 個座標為
v . vj
例
求向量(5, 10) 在基 S = {(3/5, 4/5), (-4/5, 3/5)}中的座標。
(5,10).(3/5,4/5) = 11
(5,10).(-4/5, 3/5) = 2
[(5,10)]S = (11,2)
給定一個空間向量,求出以這個向量為軸的正交基
解
假設給定的空間向量為
v = (a,b,c);
則與v垂直的向量必定滿足
a*x + b*y + c*z = 0
這個向量可以是u = (0;-c;b) 或者 u = (-c,0,a);
已知兩個向量,第三個向量利用向量叉乘就可以得出
w = cross(u,v)
最後將u,v,w單位化,得到新的正交基。
不同正交基下的座標變換
同一個向量,在不同的基下面的座標是不同的。因此,可以用正交矩陣來代表座標系(也可以看作基)從而寫出在統一的參考系(全域性座標系)下同一個向量在不同基中的座標。

已知一個基Q和向量v在它之中的座標v’,以及另外一個基R,我們可以通過v=Qv’=Rv’’公式來計算v’’。

上面就是求v’’的公式,注意到右邊需要計算基R的逆矩陣R^-1,因為基R是正交矩陣,而正交矩陣的一個重要性質就是逆等於轉置。因此,我們可以把它寫成
![]()
這個公式就是座標轉換公式。特別地,如果Q是和參考系相同的座標系(3D程式設計中大多數情況下如此),比如世界座標系,則Q是一個單位矩陣I,則我們可以把它寫成
![]()
這個座標轉換公式可以解釋為:對於世界座標系中的向量v’,它在座標系R中的座標是v’’
我們還可以得到喲個有趣的結論:
假設原始的座標系為x-(1,0,0), y-(0,1,0), z(0,0,1),這個座標系經過一個旋轉矩陣Matrix旋轉之後,新的座標系就是這個旋轉矩陣的轉置三個列向量。
圓柱體的射線求交
上面囉嗦到的兩個地方這裡都會用到。
首先還是定義圓柱體的類
public class Cylinder : NGeometry
{
public Vector3 p0;
public Vector3 p1;
public float radius;
public Cylinder(Vector3 _p0, Vector3 _p1, float _radius)
: base(GeometryType.Cylinder)
{
p0 = _p0;
p1 = _p1;
radius = _radius;
}
public Cylinder() : base(GeometryType.Cylinder) { }
public Vector3 ComputeDirection()
{
return p1 - p0;
}
}看檢測的程式碼,有點長
public static bool Raycast(Ray ray, float distance, Cylinder cylinder, out RaycastHitInfo hitInfo)
{
hitInfo = new RaycastHitInfo();
Vector3 cylinderDir = cylinder.ComputeDirection();
Vector3 kW = cylinderDir;
float fWLength = kW.magnitude;
kW.Normalize();
//two thin for check
if (fWLength <= 1e-6f)
{
return false;
}
//generate orthonormal basis
//cylinder along the z direction
Vector3 kU = Vector3.zero;
if (fWLength > 0.0f)
{
float fInvLength;
if (Mathf.Abs(kW.x) >= Mathf.Abs(kW.y))
{
fInvLength = 1.0f / Mathf.Sqrt(kW.x * kW.x + kW.z * kW.z);
kU.x = -kW.z * fInvLength;
kU.y = 0.0f;
kU.z = kW.x * fInvLength;
}
else
{
// W.y or W.z is the largest magnitude component, swap them
fInvLength = 1.0f / Mathf.Sqrt(kW.y * kW.y + kW.z * kW.z);
kU.x = 0.0f;
kU.y = kW.z * fInvLength;
kU.z = -kW.y * fInvLength;
}
}
Vector3 kV = Vector3.Cross(kW, kU);
kV.Normalize();
// compute intersection
//Transform the ray to the cylinder's local coordinate
//new Ray direction
Vector3 kD = new Vector3(Vector3.Dot(kU, ray.direction), Vector3.Dot(kV, ray.direction), Vector3.Dot(kW, ray.direction));
float fDLength = kD.magnitude;
Debug.Log("fDLength: " + fDLength);
kD.Normalize();
float fInvDLength = 1.0f / fDLength;
Vector3 kDiff = ray.origin - cylinder.p0;
//new Ray origin
Vector3 kP = new Vector3(Vector3.Dot(kU, kDiff), Vector3.Dot(kV, kDiff), Vector3.Dot(kW, kDiff));
float fRadiusSqr = cylinder.radius * cylinder.radius;
// Is the ray direction parallel to the cylinder direction? (or zero)
if (Mathf.Abs(kD.z) >= 1.0f - Mathf.Epsilon || fDLength < Mathf.Epsilon)
{
float fAxisDir = Vector4.Dot(ray.direction, cylinderDir);
float fDiscr = fRadiusSqr - kP.x * kP.x - kP.y * kP.y;
// ray direction anti-parallel to the cylinder direction
if (fAxisDir < 0 && fDiscr >= 0.0f)
{
if (kP.z > fWLength)
{
hitInfo.distance = (kP.z - fWLength) * fInvDLength;
}
else if (kP.z < 0)
{
return false;
}
else if (kP.z > 0 && kP.z < fWLength)
{
hitInfo.distance = kP.z * fInvDLength;
}
if (hitInfo.distance > distance)
return false;
hitInfo.point = hitInfo.distance * ray.direction;
return true;
}
// ray direction parallel to the cylinder direction
else if (fAxisDir > 0 && fDiscr >= 0.0f)
{
if (kP.z > fWLength)
{
return false;
}
else if (kP.z < 0)
{
hitInfo.distance = -kP.z * fInvDLength;
}
else if (kP.z > 0 && kP.z < fWLength)
{
hitInfo.distance = (fWLength - kP.z) * fInvDLength;
}
if (hitInfo.distance > distance)
return false;
hitInfo.point = hitInfo.distance * ray.direction;
return true;
}
else
{
//ray origin out of the circle
return false;
}
}
// test intersection with infinite cylinder
// set up quadratic Q(t) = a*t^2 + 2*b*t + c
float fA = kD.x * kD.x + kD.y * kD.y;
float fB = kP.x * kD.x + kP.y * kD.y;
float fC = kP.x * kP.x + kP.y * kP.y - fRadiusSqr;
float delta = fB * fB - fA * fC;
// line does not intersect infinite cylinder
if (delta < 0.0f)
{
return false;
}
// line intersects infinite cylinder in two points
if (delta > 0.0f)
{
float fRoot = Mathf.Sqrt(delta);
float fInv = 1.0f / fA;
float fT = (-fB - fRoot) * fInv;
float fTmp = kP.z + fT * kD.z;
float dist0 = 0f, dist1 = 0f;
float fT1 = (-fB + fRoot) * fInv;
float fTmp1 = kP.z + fT * kD.z;
//cast two point
//fTmp <= fWLength to check intersect point between slab.
if ((0.0f <= fTmp && fTmp <= fWLength) && (0.0f <= fTmp1 && fTmp1 <= fWLength))
{
dist0 = fT * fInvDLength;
dist1 = fT1 * fInvDLength;
hitInfo.distance = Mathf.Min(dist0, dist1);
return true;
}
else if ((0.0f <= fTmp && fTmp <= fWLength))
{
dist0 = fT * fInvDLength;
hitInfo.distance = dist0;
return true;
}
else if ((0.0f <= fTmp1 && fTmp1 <= fWLength))
{
dist1 = fT1 * fInvDLength;
hitInfo.distance = dist1;
return true;
}
//If intersect the infinite cylinder but point not between slab, the ray may intersect cylinder's caps.
//Test intersection with caps
float deltaAngle = Vector4.Dot(ray.direction, cylinderDir);
// Ray direction anti-parallel to the capsule direction
if (deltaAngle < 0)
{
if (kP.z > fWLength)
{
float deltaZ = kP.z - fWLength;
float angle = Vector3.Angle(ray.direction, -cylinderDir);
hitInfo.distance = (kP.z - fWLength) * fInvDLength / Mathf.Cos(angle * Mathf.Deg2Rad);
}
else if (kP.z < 0)
{
Debug.Log("No cap0");
return false;
}
if (hitInfo.distance > distance)
return false;
hitInfo.point = ray.origin + hitInfo.distance * ray.direction;
if (Vector3.Distance(hitInfo.point, cylinder.p1) > cylinder.radius)
{
return false;
}
return true;
}
// Direction parallel to the cylinder direction
else if (deltaAngle > 0)
{
if (kP.z > fWLength)
{
Debug.Log("No cap1");
return false;
}
else if (kP.z < 0)
{
float angle = Vector3.Angle(ray.direction, cylinderDir);
hitInfo.distance = -kP.z * fInvDLength / Mathf.Cos(angle * Mathf.Deg2Rad);
}
if (hitInfo.distance > distance)
return false;
hitInfo.point = ray.origin + hitInfo.distance * ray.direction;
if (Vector3.Distance(hitInfo.point, cylinder.p0) > cylinder.radius)
{
return false;
}
return true;
}
}
// line is tangent to infinite cylinder
else
{
float fT = -fB / fA;
float fTmp = kP.z + fT * kD.z;
if (0.0f <= fTmp && fTmp <= fWLength)
{
hitInfo.distance = fT * fInvDLength;
return true;
}
}
return false;
}簡單梳理一下流程
1.將座標系轉換到了以圓柱體方向為軸的座標系,用的就是給定一個空間向量,求出以這個向量為軸的正交基中提到的方法;
2.將Ray的origin和Direction都轉到新的座標系下,用的是上面的定理2。新的ray的origin為kP,direction為kD,射線上的點可以表示為kP+t*kD;
3.判斷射線方向是否與Z軸方向平行,如果是,判斷是否是圓柱體的上下面相交;
4.判斷是否是圓柱相交,這裡先假設圓柱是無限的,判斷的方法是求解二次方程。這裡詳細說一下,二次函式的形式為
Q(t) = a*t^2 + 2*b*t + c
假設設想和圓柱相交,則必定存在射線上存在t,滿足點kP+t*kD到Z軸的距離為圓柱的半徑
(kP.x +t*kD.x)^2 +(kP.y +t*kD.y)^2 = R^2
先通過delta判斷根的個數,最後求解就可以得到結果。
測試程式碼
using UnityEngine;
using System.Collections;
using NPhysX;
public class RayCylinderTester : MonoBehaviour {
public GameObject cylinder;
Cylinder _cylinder;
Ray ray;
float castDistance = 10f;
// Use this for initialization
void Start () {
_cylinder = new Cylinder();
}
// Update is called once per frame
void Update () {
ray = new Ray(Vector3.zero, new Vector3(1, 1, 1));
_cylinder.radius = 0.5f * cylinder.transform.localScale.x;
_cylinder.p0 = cylinder.transform.position + cylinder.transform.rotation * Vector3.down * cylinder.transform.localScale.y;
_cylinder.p1 = cylinder.transform.position + cylinder.transform.rotation * Vector3.up * cylinder.transform.localScale.y;
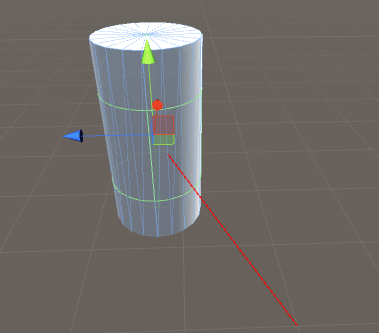
Debug.DrawLine(_cylinder.p0, _cylinder.p1, Color.green);
RaycastHitInfo hitinfo = new RaycastHitInfo();
if (NRaycastTests.Raycast(ray, castDistance, _cylinder, out hitinfo))
{
Debug.DrawLine(ray.origin, ray.origin + ray.direction * hitinfo.distance, Color.red, 0, true);
}
else
{
Debug.DrawLine(ray.origin, ray.origin + ray.direction * castDistance, Color.blue, 0, true);
}
}
}
參考
Orthonormal Bases in Rn - http://ltcconline.net/greenl/courses/203/vectors/orthonormalbases.htm
PhysX 3.3 source code
Create orthonormal basis from a given vector - http://www.mathworks.com/matlabcentral/answers/72631-create-orthonormal-basis-from-a-given-vector
推導相機變換矩陣 - http://blog.csdn.net/popy007/article/details/5120158