昨天參加了CVTE的線上筆試，由於隔了很久沒有接觸C語言了，C++自學的狀態也不是很好，再加上最近搞畢設腦袋裡全是MATLAB的語法等。筆試狀態不是很好，程式設計題挺簡單的，但是由於時間心態原因做的不對或者不全，特私下自己改正了下。前面部分是自己寫的不優秀的程式碼，後面部分是參考資料後改善的程式碼，有關複雜度的改善見本文後段。

        由於是C++初學者，程式碼有哪些不合適或者可以簡便些的地方，還望讀者能夠指出，我們一起討論與學習。

1.輸入一個整型陣列，數組裡有正數也有負數。陣列中連續的一個或多個整陣列成一個子陣列，每個子陣列都有一個“和”。輸出所有子陣列中“和”最大的子陣列。要求時間複雜度為O

完整程式：

#include<iostream>
#include<stdlib.h>
using namespace std;
int main()
{
int max=0;
int N;
int num2=0;
int num1=0;
int *arr;
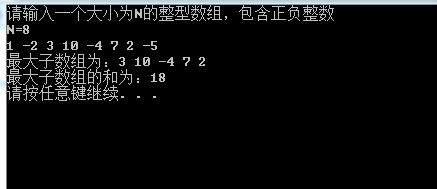
cout<<"請輸入一個大小為N的整型陣列，包含正負整數"<<endl;
cout<<"N=";
cin>>N;
arr=new int[N];
for(int k=0;k<N;k++)
{
cin>>arr[k];
}
for(int i=0;i<N;i++)
{
int temp=0;
for(int j=i;j<N;j++)
{
temp+=arr[j];


if(temp>max)
{
max=temp;//如果多加了數的值比MAX大，則將該較大的值賦給MAX
num2=j;
num1=i;
} 
}
}
cout<<"最大子陣列為：";
for(int m=num1;m<=num2;m++)
{
cout<<arr[m]<<" ";
}
cout<<endl<<"最大子陣列的和為："<<max<<endl;
system("pause");
return 0;
}

執行結果：

2.一個允許重複，長度為N的整型陣列，請找出現次數超過N/2的第一個數字。請實現此函式：int getResult(int *array,int length);

完整程式：

#include<iostream>
#include<stdlib.h>
using namespace std;
int getResult(int *array,int length);
int main()
{
int arr[]={3,5,4,3,3};
int theNum;
theNum=getResult(arr,5);
cout<<"出現次數超過N/2的數字是："<<theNum<<endl;
system("pause");
return 0;
}
int getResult(int *array,int length)
{
int temp=0;
int theNum=0;
for(int i=0;i<(length+1)/2;i++)
{
int num=1;
temp=array[i];
for(int j=i+1;j<length;j++)
{
if(array[j]==temp)
++num;
}
if(num>length/2)
{
theNum=temp;
break;
}
}
    return theNum;
}

執行結果：

演算法時間複雜度的問題分析

時間複雜度是總運算次數表示式中受n的變化影響最大的那一項(不含係數)
比如：一般總運算次數表示式類似於這樣：a*2^n+b*n^3+c*n^2+d*n*lg(n)+e*n+f，a ！ =0時，時間複雜度就是O(2^n)。

eg:
(1)   for(i=1;i<=n;i++)   //迴圈了n*n次，當然是O(n^2)
            for(j=1;j<=n;j++)
                 s++;
(2)   for(i=1;i<=n;i++)//迴圈了(n+n-1+n-2+...+1)≈(n^2)/2，因為時間複雜度是不考慮係數的，所以也是O(n^2)
            for(j=i;j<=n;j++)
                 s++;
(3)   for(i=1;i<=n;i++)//迴圈了(1+2+3+...+n)≈(n^2)/2,當然也是O(n^2)
            for(j=1;j<=i;j++)
                 s++;
(4)   i=1;k=0;
      while(i<=n-1){
           k+=10*i;
      i++;      }
//迴圈了
n-1≈n次，所以是O(n)
(5)   for(i=1;i<=n;i++)
             for(j=1;j<=i;j++)
                 for(k=1;k<=j;k++)
                       x=x+1;
//
迴圈了(1^2+2^2+3^2+...+n^2)=n(n+1)(2n+1)/6(這個公式要記住哦)≈(n^3)/3，不考慮係數，自然是O(n^3)

故兩個題目的演算法複雜度為0（n^2),沒有達到要求。

題目1的改進答案待定

題目2改進的答案，複雜度降低了，為O（n),符合原題要求。

#include <iostream>
using namespace std;
int getResult(int *arry,int length)
{
    int ntime = 0; //表示其中某一個數出現的次數
    int theNum;
    for( int i = 0; i <length; i++)
{
        if(ntime == 0)
{   //在i前面的數全部刪除完，或者起始的時候，將arry[i]放入結果
              theNum = arry[i];
              ntime = 1;  //arry[i]出現的次數為1；
        }
else 
{ //如果前面有數，就說明result還沒抵消完
              if(theNum == arry[i]) //如果相等result出現的次數+1
                ntime++;
              else
                ntime--;  /*如果此時的arry[i]不等於result，則它們兩個抵消，result的次數減一，由與那個數大於n/2所以它抵消不完，ntime最小為1
                            也就是說這個數出現的次數是大於等於n/2+1*/
        }
    }
    return theNum;
}
int main()
{
int arr[]={3,5,4,3,3};
int theNum;
theNum=getResult(arr,5);
cout<<"出現次數超過N/2的數字是："<<theNum<<endl;
system("pause");
return 0;
}