TensorFlow 入門

TensorFlow實現神經網路

前向傳播演算法簡介

• 神經元是構成一個神經網路的最小單元，神經元也可以稱之為節點。

  • 一個神經元有多個輸入和一個輸出；
  • 每個神經元的輸入既可以是其他神經元的輸出，也可以是整個神經網路的輸入；
  • 所謂神經網路的結構指的就是不同神經元之間的連線結構。

• 一個最簡單的神經元結構的輸出就是所有輸入的加權和，而不同輸入的權重就是神經元的引數。神經網路的優化過程就是優化神經元中引數取值的過程。

• 全連線神經網路是相鄰兩層之間任意兩個節點之間都有連線的神經網路結構。

• 一個簡單的判斷零件是否合格的三層全連線神經網路。
  

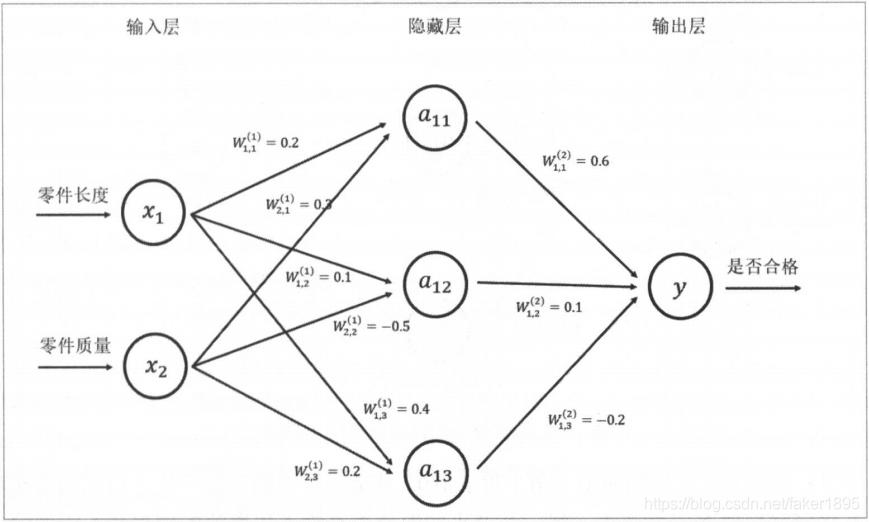
  • 計算神經網路的前向傳播結果需要三部分資訊。
    • 第一個部分是神經網路的輸入，這個輸入就是從實體中提取的特徵向量。
      • 在圖中有兩個輸入，一個是零件的長度 $x_1$
        x_1 ，一個是零件的質量 $x_2$
        x_2 。
    • 第二個部分為神經網路的連線結構。
      • 神經網路是由神經元構成的，神經網路的結構給出不同神經元之間輸入輸出的連線關係。
      • 在圖中， $a_{11}$節點有兩個輸入，他們分別是 $x_1$和 $x_2$的輸出。而 $a_{11}$的輸出則是節點 $y$的輸入。
    • 最後一個部分是每個神經元中的引數。
      • 在圖中用 $W$來表示神經元中的引數。
      • $W$的上標表明瞭神經網路的層數，比如以 $W^{(1)}$表示第一層節點的引數，而以 $W^{(2)}$表示第二層節點的引數。
      • W 的下標表明瞭連線節點編號，比如 $W_{1,2}^{(1)}$表示連線 $x_1$和 $a_{12}$節點的邊上的權重。
  • 給定神經網路的輸入、神經網路的結構以及邊上權重，就可以通過前向傳播演算法來計算出神經網路的輸出。

• 神經網路前向傳播演算法示意圖
  

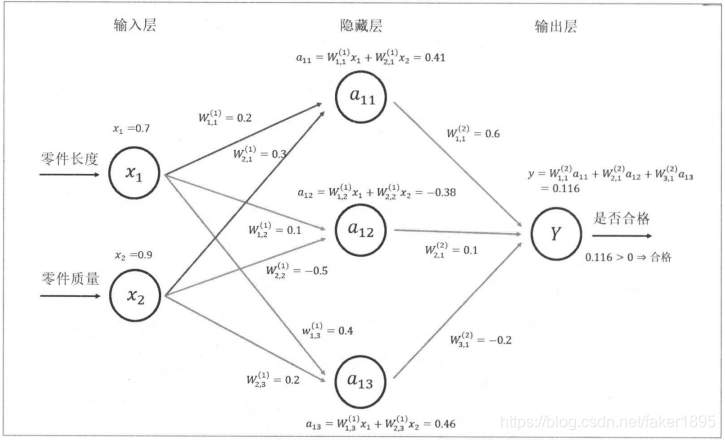
  • 圖中給出了輸入層的取值 $x_1=0.7$和 $x_2=0.9$。
  • 從輸入層開始一層一層地使用向前傳播演算法。
  • 首先隱藏層中有三個節點，每一個節點的取值都是輸入層取值的加權和。
  • 在得到第一層節點的取值之後，可以進一步推導得到輸出層的取值。
  • 類似地，輸出層中節點的取值就是第一層的加權和。
  • 因為這個輸出值大於閾值0，所以在這個樣例中最後給出的答案是：這個產品是合格的。這就是整個前向傳播的演算法。

• 前向傳播演算法可以表示為矩陣乘法。

  • 將輸入 $x_1, x_2$組織成一個 $1*2$的矩陣 $x=[x_1, x_2]$，而 $W^{(1)}$組織成一個 $2*3$的矩陣：
    $W^{(1)}= \begin{bmatrix} W_{1,1}^{(1)} & W_{1,2}^{(1)} & W_{1,3}^{(1)} \\ W_{2,1}^{(1)} & W_{2,2}^{(1)} & W_{2,3}^{(1)} \end{bmatrix}$
  • 這樣通過矩陣乘法可以得到隱藏層三個節點所組成的向量取值：
    $a^{(1)}=[a_{11}, a_{12}, a_{13}]=xW^{(1)}=[W_{1,1}^{(1)}x_1+W_{2,1}^{(1)}x_2, W_{1,2}^{(1)}x_1+W_{2,2}^{(1)}x_2, W_{1,3}^{(1)}x_1+W_{2,3}^{(1)}x_2]$