容斥原理描述如下：

說大白話就是求幾個集合的並集，要計算幾個集合並集的大小，我們要先將所有單個集合的大小計算出來，然後減去所

有兩個集合相交的部分，再加上所有三個集合相交的部分，再減去所有四個集合相交的部分...依此類推，一直計算到

所有集合相交的部分。

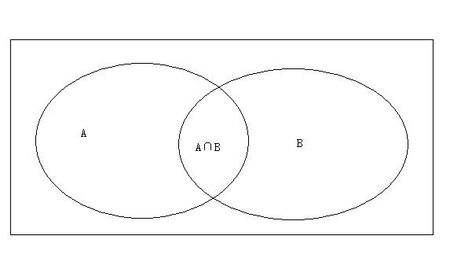
最簡單的就是兩個集合的並集：

所以數學公式就可以表示為 |A∪B|=|A|+|B|-|A∩B|。

對於三個集合，數學公式為|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|。

常用方法有兩種：遞迴法和二進位制列舉法。

遞迴法是利用dfs的思想進行搜尋，檢索每一種方案進行容斥。

二進位制列舉的方法最大的好處是能夠枚舉出所有元素組合的不同集合。假設一個集合的元素有m個，

制數來說就有m個1或0的位置，對於每一個1就對應一個元素。

整個二進位制列舉完就是所有子集，從0到2^m就行。[0, 2^m)

看下模板題HDU-1796

題意：給定一個數n，數列m個數，求這小於n的數中，有多少個數滿足能被這m個數中任意一個數整除。

思路：1~n之間有多少個能被x整除的數，公式為n/x，題目中要求小於n,所以(n-1)/x。

可以遞迴法求，需要儲存中間態重疊x次的最小公倍數lcm,符合題意的數有(n-1)/lcm個，根據k表示重疊的次數進

行或者加上，或者減去。

也可以用二進位制列舉法，將符合條件的m個數，看作m位，每位是0或者是1，那麼一共有2^m種狀態，只要判斷一下每

一個狀態有多少個1，也就是有多少個數（重疊多少次）,記為k，每一個1代表哪幾個具體的數，求這幾個數的最小

公倍數，然後(n-1)/lcm,  利用k的值來判斷應該減去還是加上即可。

Code1:

#include <bits/stdc++.h>
using namespace std;
int n, m, num[15], ans, tot, x;
int gcd(int a, int b)
{
	if(a%b == 0) return b;
	return gcd(b, a%b);
}
void dfs(int pos, int pre_lcm, int k)
{
	for(int i = pos+1; i < tot; ++i)
	{
		int lcm = pre_lcm/gcd(num[i], pre_lcm)*num[i];
		if(k&1) ans += (n-1)/lcm;
		else ans -= (n-1)/lcm;
		dfs(i, lcm, k+1);
	}
}
int main()
{
	while(~scanf("%d %d", &n, &m))
	{
		ans = 0; tot = 1;
		for(int i = 1; i <= m; ++i)
		{
			scanf("%d", &x);
			if(x > 0 && x < n) num[tot++] = x;
		}
		dfs(0, 1, 1);
		printf("%d\n", ans);
	}
	return 0;
}
 

#include <bits/stdc++.h>
using namespace std;
int n, m, x, k, tot, up, t, pos, lcm, ans, num[15];
int gcd(int a, int b)
{
	if(a%b == 0) return b;
	return gcd(b, a%b);
}
int main()
{
	while(~scanf("%d %d", &n, &m))
	{
		tot = 1; ans = 0;
		for(int i = 1; i <= m; ++i)
		{
			scanf("%d", &x);
			if(x > 0 && x < n) num[tot++] = x;
		}
 		up = (1<<(tot-1));
		for(int i = 1; i < up; ++i)
		{
			t = i, k = 0, pos = 1; lcm = 1;
			while(t)
			{
				if(t&1)
				{
					lcm = num[pos]/gcd(lcm, num[pos])*lcm;
					++k;
				}
				t >>= 1; ++pos;
			}
			if(k&1) ans += (n-1)/lcm;
			else ans -= (n-1)/lcm;
		}
		printf("%d\n", ans);
	}
	return 0;
}

圖片來自百度圖片，參考博文：