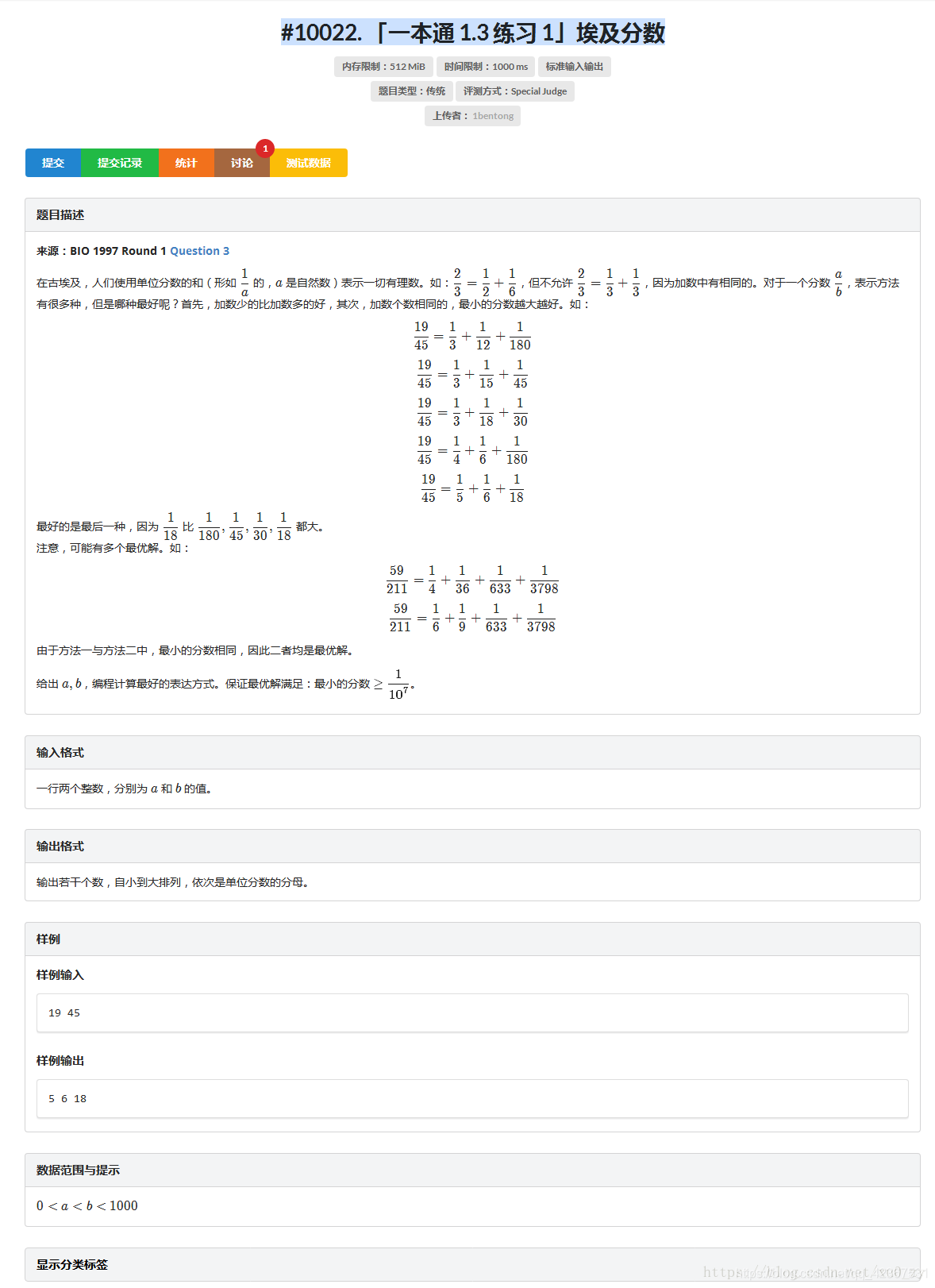
（因為題目實在是太複雜麻煩了，所以我就直接截圖了啊，望諒解） 

先理解一下題目吧（我知道大家都看懂了，那我就不多說了，按老規矩給你們稍微總結一下吧）

• 首先，這道題我們要求的是最大當中的最小，就是說最後一個的分數的分母是最大的，這個就是最大的，然後我們又要讓最大的這個分母最小。這個很關鍵因為這個關乎到了我們 dfs 當中的判斷，換個角度想想如果沒有這個的話，這道題就很簡單了，直接搜尋找到加起來的值是相同的就退出。
• 第二點就是因為這是分數，也就是說它有兩部分，這就意味著如果我們直接就用這個分數的值來搜尋的話，肯定會出問題：

1. 你在定義的時候，如果是除不盡的小數怎麼辦？
2. 我們的分子分母怎麼樣列舉，一起加還是說一起減？分開你要怎麼折騰？
3. dfs中的那個當前搜尋的層數，分子分母各定義一個還是說分開定義

所以這些都是我們要考慮的，這些看起來很白痴的問題就為我們的搜尋起到了一個極為重要的鋪墊作用、

• 最簡分數要用gcd的吧（求最大公約數的函式）
• 用來輸出的陣列要有吧
• 如果把dfs看成一棵樹的話，這個最大層數和最小層數要有吧
• 還有就是說我們在搜尋判斷的時候，更新這個儲存的陣列要有吧
• 我們搜素判斷的時候，一個bool要有吧，還有就是說dfs我們直接用bool，這樣我們就直接搜尋成功返回再輸入，如果在dfs當中進行的話，可能會出錯
• 最後的就是剪枝了吧

接下來我就重點來講一下我們的一個小小的東西（叫剪枝）

很好這是我們其中的一個要點。就是說我們的分子一定要大於等於，這個是必然的

 這是又一個點，也是我們在搜尋的時候必須知道的，所以說如果沒有這一個的話你再怎麼搜尋都是會錯的，要不超時要不就是說整個的執行的錯誤

附上大佬的部落格

整體的一些就是大概這樣的啦。剩下的我也不多講，看程式碼吧 

【程式碼實現1:我的理解性程式碼300多ms】

/*我不得不再打一遍程式碼
對於這個具體的原理我還是要好好研究一下
大概有那麼一點點思路
就是說我們在遞迴的時候一直在更改我們的分子和分母
然後我們還要判斷這麼分子和分母到底可不可以
而且還有判斷他們相加到底等不等於這個原數
如果等於的話，我們就把當前這個成功的答案記錄到c陣列當中
記錄完之後繼續尋找，繼續找更小的
這個就是這道題的主要思路*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll a,b,c[210000],shi[210000];/*a，b表示原數，c是用來記錄結果的，
shi陣列是用來記錄我們在搜尋當中找到的分母，他們的分子預設為1*/ 
int maxn,tt=99999;//maxn是我們目前確定的最大層數，tt是配套c陣列的層數 
ll zxfm(ll p,ll q)//我們搜尋到的最小層數 
{
	for(int i=2;;i++)
	{
		if(q<=p*i)return i;
	}
}
ll gcd(ll a,ll b)//最大公約數 
{
	if(a==0)return b;
	return gcd(b%a,a);
}
bool pd(int tp)//pd剪枝吧，就是不能比之前記錄過的最小值要大 
{
	if(maxn>tt)return false;
	if(shi[maxn]>c[tt])return false;
	return true; 
}
bool dfs(int d,ll minx,ll x,ll y)/*d是我們當前搜尋的層數，minx是最小層數，
x，y是第一次是原數 
x，y確切來講應該是我們在不斷的搜尋當中確定的一個個分子和分母\
然而這個分子和分母一定要是倍數關係，也就是說分子可以變為1*/
{
	if(d==maxn)//如果這個層數已經到了最大層數 
	{
		if(y%x!=0)return false;//倍數關係不是最簡，返回重新計算 
		shi[d]=y/x;//否則記錄下來他們的商 
		if(pd(d))//pd一下能不能剪枝 
		{
			for(int i=1;i<=maxn;i++)c[i]=shi[i];//成功就更新一下 
			tt=maxn;//把最大層數也更新一下 
		}
		return true;//返回上一層 
	}
	minx=max(minx,zxfm(x,y));/*我覺得主要原因是因為就是說，minx記錄的是最小層數,
	然後zxfm找到的也是最小層數，這個主要是為了後面ab更改之後在更換，因為層數越大，才表示
	我們真正的最極限的情況*/ 
	bool bkk=false;//bkk用在判斷當中 
	for(int i=minx;i;i++)
	{
		if((maxn-d+1)*y<=i*x)break;/*
		如果最大個數*最大層數(或者最大層數的上一層)[層數越往上值越大] 
		小於最小個數*最小層數的話，這個情況本身就是有問題的
		(簡單來講，這應該算是一個剪枝條件)*/ 
		shi[d]=i;//
		ll xx=x*i-y,yy=y*i,GCD=gcd(xx,yy);/*最小極限和最大極限，
		無論如何a*i-b是不等於0的，
		這個可以說是當前最小的分數的極限(分子很小，分母很大)。
		找到之後看看有沒有公約數*/ 
		if(dfs(d+1,i+1,xx/GCD,yy/GCD))bkk=true;//繼續遞迴下一層的 
	}
	return bkk;
}
int main()
{
	scanf("%lld%lld",&a,&b);//輸入 
	if(a%b==0)/*如果是倍數關係，比如說5/10的話，那麼公約數是5，他們的答案就是1/2，1和2*/ 
	{
		ll GCD=gcd(a,b);
		printf("%lld %lld",a/GCD,b/GCD);
		return 0;
	}
 	ll minn=zxfm(a,b);//找到最小層數 
	maxn=2;//maxn是最大層數，但是我暫時還不到為什麼初始化是2 
	do{//do...while的意思就是說先做了再判斷 
		memset(c,63,sizeof(c));//初始化 
		if(dfs(1,minn,a,b))//遞迴 
		{
			for(int i=1;i<=maxn;i++)printf("%d ",c[i]);
			printf("\n");//找到答案就輸出 
			return 0;
		}
		maxn++;//找不到就增加一個繼續找 
	}while(maxn);
	return 0;
}
/*總結就一句話：我他媽一直加啊加，然後除啊除，然後就找到答案了*/
 

【程式碼實現2:大佬的程式碼300多ms】

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll a[1010],s[1010],maxd;
inline ll max(ll x,ll y){return x>y?x:y;}//最大值 
inline ll get(ll aa,ll bb){return bb/aa+1;}//函式函式 
ll gcd(ll aa,ll bb){return (!bb)?aa:gcd(bb,aa%bb);}//最大公約數 
bool bijiao(ll x)
{
    for(ll i=x;i>=0;i--) 
        if(a[i]!=s[i])return s[i]<0||a[i]<s[i];
    return false;
}
bool dfs(ll k,ll fa,ll aa,ll bb)
{
    if(k==maxd)
    {
        if(bb%aa)return false;
        a[k]=bb/aa;
        if(bijiao(k))
        { 
            for(ll i=0;i<=k+1;i++)
			{
				s[i]=a[i];
			}
		}
        return true;
    }
    else
    {
        bool bk=false;
        fa=max(fa,get(aa,bb));
        for(ll i=fa;;i++)
        {
            if((maxd+1-k)*bb<=aa*i)break;
            a[k]=i;
            ll ax=aa*i-bb,bx=bb*i;
            ll gg=gcd(ax,bx);
            if(dfs(k+1,i+1,ax/gg,bx/gg))bk=true;
        }
        return bk;
    }
}
int main()
{
    ll a,b;scanf("%lld%lld",&a,&b);
    bool bk=false;
    for(maxd=1;maxd<=100;maxd++)
    {
        memset(s,-1,sizeof(s));
        if(dfs(0,get(a,b),a,b)){bk=true;break;}
    }
    if(bk)
    {
        for(ll i=0;i<maxd;i++)printf("%lld ",s[i]);
        printf("%lld\n",s[maxd]);
    }
    return 0;
}

 大致就結束了吧，謝謝。