簡單易懂的Dancing links講解(4)
DancingLinks的應用
把dancingLink應用於實際問題時,只有一個難點,就是如何把具體的問題轉換為可以精確覆蓋的01矩陣模型,一旦完成了這個步後,直接套用模板就可以解決問題了。
應用之一:傷腦筋十二塊
傷腦筋十二塊是dancing links精確覆蓋的典型應用,理解起來最容易
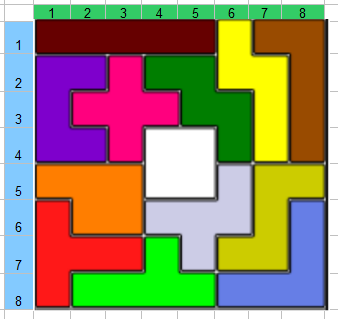
圖2,12片5格骨牌的拼圖
題目描述:
給你12個如上圖的5格骨牌,如何讓程式拼出如上的“口”字圖形。
上圖是題目的一個答案,你知道程式如何得到這個答案的嗎?沒錯,就是用dancinglink的精確覆蓋
我們想象一個有72列的矩陣,其中12列是12個骨牌,剩下60列是60個非中心部分的格子,構造出
所有可能的行來代表在一塊骨牌在棋盤上得放置方案;每行有一些‘’1“,用來標識被覆蓋的格子,5個1標識一個骨牌放置的位置(恰有1568個這樣的行)
我們將最前面的12列命名為F,I,L,P,N,T,U,V,W,X,Y,Z,並且我們可以用兩個數字i,j給矩陣中對應棋盤上的第i行第j列格子的那一列命名。通過給出那些出現了‘’1"的列的名字,可以很方便地表示每一行。
例如,圖2就是與下面12行的對應的精確覆蓋。

1568個行指的是12個骨牌可放置方案的總和,比如長條骨牌I共有64种放置方案,1568中就包含了這64種
這1568行中,每行都有6個1,分佈在72個列中
這個矩陣的構造思路是:
首先找約束關係,這裡只有兩個約束關係,
(1)12個骨牌,每種只有1個,
(2)60個空格中,一個位置只能放一種骨牌(否則就要重疊著放了)
因為第一個約束關係,有了12個列來區分骨牌種類,因為第二個約束關係,有了60個選5個來表示骨牌放置
應用之二:數獨問題 sudoku
解數獨,生成數獨,都可以使用精確覆蓋,要把數獨問題構造成01矩陣還是有一定的難度
首先找約束關係,這裡只有四個約束關係,
(1)81個格子中每個格子只能放一個數字
(2)每一行的數字不能重複
(3)每一列的數字不能重複
(4)每一九宮內的數字不能重複

四個約束關係中,每個約束對應一個列域,對於第二個約束關係,數獨中共有9行,每行可以填9個不同的數字
因此第二個列域,共有9* 9,81個列,依此類推,數獨問題共有列324個。
由於81個格子,每個格子都最多有9種選擇,所以行最多有81*9=729行
這樣01矩陣的每行都有4個1,第一個1分佈在1到81列,第二個1分佈在82到162列,第三個1分佈在163到243列,
最後一個1分佈在其餘列區域。
思考:為什麼不能這樣構造01矩陣,用5個1,第一個1表示格子序號,有81個列,第二個1表示數字,從1到9有9個列,第三個1表示行號,有9行,第四個1表示列號也有9個,第五個1表示九宮格序號,也有9個,這樣共有117列。
為了便於理解,舉個例子
9,2,0,0,0,0,0,0,0,
5,0,0,8,7,0,0,0,0,
0,3,8,0,9,1,0,0,0,
0,5,2,9,3,0,1,6,0,
0,9,0,0,0,0,0,3,0,
0,7,3,0,6,4,9,8,0,
0,0,0,4,1,0,2,5,0,
0,0,0,0,5,3,0,0,1,
0,0,0,0,0,0,0,7,3
如上數獨有空格40個,已知格子41個,把這個數獨構造成01矩陣,矩陣的行有
40*9+41 共401行
對於第一個數字9,在1到81列的第一列,在82到162列的第9個,即90列,在163列到243列的第9個,在244到324列的第9個各佔一個1
對於第三個數字0,由於有9個選擇,所以在構造01矩陣時,要向矩陣插入9個行,來表示各種可能
對於第四個數字8,它在二行四列,把這個數字寫入dancing link的網狀資料結構時,需要新增四個節點,這四個節點都在同一行,它們的列序號分別為,
13, 81 + 9 + 8 - 1,81 + 81 + 3 * 9 + 8 - 1,81 + 81 + 81 + 9 + 8 - 1, 序號是從0開始的,所有要減去一。
現在假設,2行6列的空格是數字8,那麼這個數字也會對應四個節點,列序號分別為
15,81 + 9 + 8 - 1, 81 + 81 + 5 * 9 + 8 - 1, 81 + 81 + 81 + 9 + 8 - 1,
可以看到, 這兩個8的 行域,九宮格域都是相同的,表示這兩個數字的行和九宮格都相沖了,四個列域,只要有一個相沖,兩條記錄就不能共存。這兩個8顯然不能共存。
數獨還有一個變種,對角線數獨,兩條對角線的數字也不能重複,這時構造01矩陣模型時,就需要額外增加兩個列域,左對角線域,右對角線域。增加的兩個列域都只有9列,
對於1行1列的數字,會在01矩陣模型中對應5個節點,
對於2行3列的數字,由於不位於兩條對角線上,會在01矩陣模型中只對應4個節點,
對於5行5列的數字,恰好在兩條對角線的交匯處,會在01矩陣模型中對應6個節點
對於數獨的生成
總體思路是一行一行的生成,第一行可以用一個隨機的1到9的排列,接下來的8行,每行都要用dancinglink求解可行的排序
(1)先對1到9這9個數進行隨機排列,把這個排列作為數獨終盤佈局的第一行
(2)自己寫函式篩選出下一行,每個格子可以填寫的數字集合,篩選時不用考慮行衝突
比如對於排列5,9,7,4,2,6,8,3,1
篩選結果如下: 123468,123468,123468,135789,135789,135789,245679,245679,245679
表示對於下一行的1,2,3列,可以選擇的數字集合有1,2,3,4,6,8.
下一行的4,5,6列,可以選擇的數字集合有1,3,5,7,8,9
下一行的7,8,9列,可以選擇的數字集合有2,4,5,6,7,9
這時,構造01矩陣,就只有2個約束關係
1 對於下一行的9個格子,每個格子只能放一個數字
2 對於下一行的9個格子中的數字,每個數字都不能重複
因為第3個和4個約束,已經在篩選時考慮進去,這裡不需再多此一舉
這時的01矩陣,列有9+ 9=18個,行有6* 9 = 54行(6+6+6+6+6+6+6+6+6)。
應用之三:N皇后
N皇后問題也可以轉換為dancinglinks的精確覆蓋問題
這裡只講如何把n皇后問題轉換為01矩陣,首先有四個約束關係
(1)所有皇后不能在同一行
(2)所有皇后不能在同一列
(3)所有皇后不能在同一左斜線
(4)所有皇后不能在同一右斜線
為了便於理解,舉個例子
n=8時,有8行,8列,15個左斜線,15個右斜線(2*n-1)
這樣構造的矩陣有46個列,8*8=64個行
矩陣的每行都有4個1,分別分佈在行域,列域,左斜線域,右斜線域
在程式設計求解這個問題時,需要做一點變通,因為左斜線域,右斜線域的列不可能被全部覆蓋
因此只需行域和列域被完全覆蓋就算找到問題的一個解了。
附:
dancing LInks 求解數獨的C++程式碼
#include<iostream>
#include<string.h>
using namespace std;
struct Node
{
Node *up;
Node *down;
Node *left;
Node *right;
Node *colRoot; //列首
int row; //所在行
int sum; //此列節點總數
};
#define R 729
#define C 324
class Dlx
{
public:
Node *nodes,*row,*col,*head;//可用節點,行首,列首,總頭節點
int rowNum,colNum,nodeCount;//行數,列數,總節點數
int *result,resultCount;//結果,結果行數
Dlx()
{
nodes=new Node[R*C];//直接用陣列竟然執行不起,棧溢位了,還得放在堆裡
row=new Node[R];
col=new Node[C+1];
result=new int[R];
}
~Dlx()
{
delete []nodes;
delete []row;
delete []col;
delete []result;
}
void init(int r,int c);//初始化
void cover(Node *t);//覆蓋一列
void uncover(Node *t);//取消覆蓋
bool solove(int k=0);//搜尋出結果
void addNode(int r,int c);//新增一個節點
};
void Dlx::init(int r,int c)
{
int i;
rowNum=r;
colNum=c;
//將各列連起來,col[colNum]為總頭節點
for(i=0;i<=colNum;i++)
{
col[i].up=col[i].down=col+i;
col[i].left=col + (i+colNum)%(1+colNum);
col[i].right=col + (i+1)%(1+colNum);
col[i].sum=0;
}
head=col+colNum;
//將各行節點數清零
for(i=0;i<rowNum;i++)
{
row[i].up=row[i].down=row[i].left=row[i].right=row[i].colRoot=row+i;
}
nodeCount=0;//總節點數清零
}
void Dlx::addNode(int r,int c)
{
nodes[nodeCount].up=col[c].up;
nodes[nodeCount].down=col+c;
nodes[nodeCount].left=row[r].left;
nodes[nodeCount].right=row+r;
nodes[nodeCount].row=r;
nodes[nodeCount].colRoot=col+c;
col[c].up=col[c].up->down=row[r].left=row[r].left->right=nodes+nodeCount++;
col[c].sum++;
}
void Dlx::cover(Node *t)
{
Node *p,*q;
t->left->right=t->right;
t->right->left=t->left;
for(p=t->down;p!=t;p=p->down)
{
for(q=p->right;q!=p;q=q->right)
{
q->up->down=q->down;
q->down->up=q->up;
q->colRoot->sum--;
}
}
}
void Dlx::uncover(Node *t)
{
Node *p,*q;
for(p=t->up;p!=t;p=p->up)
{
for(q=p->left;q!=p;q=q->left)
{
q->up->down=q->down->up=q;
q->colRoot->sum++;
}
}
t->left->right=t->right->left=t;
}
bool Dlx::solove(int k)
{
//是否還有未覆蓋的列
if(head->right==head)
{
//記錄完成覆蓋所用行數
resultCount=k;
return true;
}
Node *pMin,*p,*q;
//找到節點數最少的一列,並覆蓋
for(pMin=head->right,p=pMin->right;p!=head;p=p->right)
{
if(pMin->sum>p->sum)
pMin=p;
}
cover(pMin);
for(p=pMin->down;p!=pMin;p=p->down)
{
result[k]=p->row;
//選定此列上的一個節點,將此節點所在行上所有節點的對應列進行覆蓋
for(q=p->right;q!=p;q=q->right)
cover(q->colRoot);
if(solove(k+1))
return true;
//如果不能成功,則取消覆蓋
for(q=p->left;q!=p;q=q->left)
uncover(q->colRoot);
}
uncover(pMin);
return false;
}
int getRowIndex(int rowNum)
{
int num = rowNum%9;
int rowIndex = rowNum / 81;
return 81 + rowIndex*9 + num;
}
int getColIndex(int rowNum)
{
int num = rowNum%9;
int index = rowNum/9; //位置
int colIndex = index%9;
return 162 + colIndex*9+num;
}
int getSquareIndex(int rowNum)
{
int num = rowNum%9;
int index = rowNum/9; //位置
int rowIndex = index / 9;
int colIndex = index%9;
int squareIndex = int(rowIndex/3)*3 + colIndex/3;
return 243 + squareIndex*9+num;
}
int main3()
{
int i,j;
int node4=0;
char str[82];
Dlx dlx;
//cin>>n;
dlx.init(729,324);
//for(i=0;i<9;i++)
//{
// cin>> (str+i*9);
//}
//......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
const char *input = ".2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.";
strcpy(str,input);
for(i=0;i<729;i++)
{
//cout << "row=>" << i << "\tcol=> 位置" << i/9 <<"\t行"<<81+i/9/9*9+i%9<<"\t列"<<162+i/9%9*9+i%9<<"\t塊"<< 243+(i/9/9/3*3+i/9%9/3)*9+i%9;
//cout << "row=>" << i << "\tcol=> 位置" << i/9 <<"\t行"<<getRowIndex(i)<<"\t列"<<getColIndex(i)<<"\t塊"<<getSquareIndex(i);
if(str[i/9]=='.' || str[i/9]-'1'==i%9)
{
node4++;
int rowIndex = i;
int colIndex = i/9;
dlx.addNode(rowIndex,colIndex);//位置衝突
dlx.addNode(rowIndex,getRowIndex(i));//行衝突
dlx.addNode(rowIndex,getColIndex(i));//列衝突
dlx.addNode(rowIndex,getSquareIndex(i));//塊衝突
// cout << "\t<=";
}
//cout << endl;
}
if(dlx.solove())
{
//結果存到字串中
for(i=0;i<81;i++)
{
j=dlx.result[i];
str[j/9]='1'+j%9;
}
//輸出字串
for(i=0;i<9;i++)
{
for(j=0;j<9;j++)
cout<<str[i*9+j];
cout<<endl;
}
}
return 0;
}附,生成數獨終盤佈局的Flex程式碼
<?xml version="1.0" encoding="utf-8"?>
<s:WindowedApplication xmlns:fx="http://ns.adobe.com/mxml/2009"
xmlns:s="library://ns.adobe.com/flex/spark"
xmlns:mx="library://ns.adobe.com/flex/mx">
<fx:Declarations>
<!-- Place non-visual elements (e.g., services, value objects) here -->
</fx:Declarations>
<fx:Script>
<![CDATA[
import model.DancingNode;
private var sample:String="1279,2367,1369,24789,4578,259,13458,1368,456";
private var rowArr:Array=[];
private var colArr:Array=[];
private var head:DancingNode;
private var nodes:Array=[];
private var cnt:Array=[];
private var answer:Array=[];
private var answerArr:Array=[];
private function _init(restrict:String):void
{
answerArr=[];
answer=[];
cnt=[];
nodes=[];
rowArr=[];
colArr=[];
var i:int;
var colLen:int=18;
var rowLen:int=restrict.split(',').join('').length;
for(i=0;i<rowLen;i++)
{
var row:DancingNode = new DancingNode(i);
rowArr.push(row);
}
for(i=0;i<=colLen;i++)
{
var col:DancingNode = new DancingNode(-1,i);
colArr.push(col);
cnt.push(0);
}
var colArrLen:int = colArr.length;
for(i=0;i<colArr.length;i++)
{
var left:int = (i+colArrLen-1)%colArrLen;
var right:int = (i+1)%colArrLen;
DancingNode(colArr[i]).left=colArr[left];
DancingNode(colArr[i]).right=colArr[right];
}
head = colArr[0];
//create links
var rowIndex:int=0;
var arr1:Array = restrict.split(',');
for(i=0;i<arr1.length;i++)
{
var arr2:Array = String(arr1[i]).split('');
for(var j:int=0;j<arr2.length;j++)
{
var colIndex1:int=i+1;
var colIndex2:int=9+int(arr2[j]);
addNode(rowIndex,colIndex1,i,int(arr2[j]));
addNode(rowIndex,colIndex2,i,int(arr2[j]));
rowIndex++;
}
}
for(i=0;i<rowLen;i++)
{
DancingNode(rowArr[i]).left.right=DancingNode(rowArr[i]).right;
DancingNode(rowArr[i]).right.left=DancingNode(rowArr[i]).left;
}
}
private function addNode(r:int,c:int,r1:int,c1:int):void
{
var node:DancingNode = new DancingNode(r,c);
node.rowValue=r1;
node.colValue=c1;
node.up = colArr[c].up;
node.down = colArr[c];
node.left = rowArr[r].left;
node.right = rowArr[r];
cnt[c]++;
colArr[c].up=colArr[c].up.down=rowArr[r].left=rowArr[r].left.right=node;
nodes.push(node);
}
private function remove(node:DancingNode):void
{
//trace("remove=>",node.col);
node.left.right = node.right;
node.right.left = node.left;
for(var p:DancingNode=node.down;p!=node;p=p.down)
{
for(var q:DancingNode=p.right;q!=p;q=q.right)
{
q.up.down=q.down;
q.down.up=q.up;
cnt[q.col]--;
}
}
}
private function resume(node:DancingNode):void
{
//trace("resume=>",node.col);
for(var p:DancingNode=node.down;p!=node;p=p.down)
{
for(var q:DancingNode=p.right;q!=p;q=q.right)
{
q.up.down=q;
q.down.up=q;
cnt[q.col]++;
}
}
node.left.right = node;
node.right.left = node;
}
private function dancing(depth:int):Boolean
{
//是否還有未覆蓋的列
if(head.right==head)
{
var arr:Array=[];
for(var i:int=0;i<answer.length;i++)
{
var node:DancingNode=answer[i];
arr[node.rowValue]=node.colValue;
}
answerArr.push(arr);
return true;
}
var pMin:DancingNode;
var p:DancingNode;
//找到節點數最少的一列,並覆蓋
for(pMin=head.right,p=pMin.right;p!=head;p=p.right)
{
if(cnt[pMin.col] > cnt[p.col])
{
pMin = p;
}
}
remove(pMin);
var q:DancingNode;
for(p=pMin.down;p!=pMin;p=p.down)
{
//選定此列上的一個節點,將此節點所在行上所有節點的對應列進行覆蓋
answer[depth]=p;
for(q=p.right;q!=p;q=q.right)
{
remove(colArr[q.col]);
}
if(dancing(depth+1))
{
if(answerArr.length > 10)
{
return true;
}
}
for(q=p.left;q!=p;q=q.left)
{
resume(colArr[q.col]);
}
}
resume(pMin);
if(answerArr.length > 0)
{
return true;
}
return false;
}
private function getSudokuLine(restricts:Array):Array
{
var arr:Array=[];
for(var i:int=0;i<restricts.length;i++)
{
arr.push((restricts[i] as Array).join(''));
}
_init(arr.join(','));
if(dancing(0))
{
var line:Array = answerArr[int(answerArr.length*Math.random())];
trace('getSudokuLine,answer length=>',answerArr.length);
return line;
}
return [];
}
//得到隨機的1到9的排列
private function getRandomArr(value:int):Array
{
var bak:Array = [];
for(var i:int=1;i<=value;i++)
{
bak.push(i);
}
var randLine:Array=[];
while(bak.length>0)
{
var index:int = bak.length*Math.random();
randLine.push(bak[index]);
bak.splice(index,1);
}
return randLine;
}
public function createFullSudoku():Array
{
var sudokuArr:Array=[];
while(sudokuArr.length < 9)
{
sudokuArr=[];
sudokuArr.push(getRandomArr(9));
for(var i:int=0;i<8;i++)
{
var restricts:Array = getRestricts(sudokuArr);
if(restricts.length==0)
{
break;
}
var line:Array = getSudokuLine(restricts);
if(line.length==0)
{
break;
}
sudokuArr.push(line);
}
}
return sudokuArr;
}
private function getRestricts(curLayout:Array):Array
{
var i:int;
var ret:Array=[];
for(i=0;i<9;i++)
{
var arr:Array=getCandidateNums(curLayout,i);
if(arr.length==0)
{
return [];
}
ret.push(arr);
}
return ret;
}
//根據當前佈局curLayout,得到index列的候選數集合
private function getCandidateNums(curLayout:Array,index:int):Array
{
var i:int;
var line:Array = [0,1,2,3,4,5,6,7,8,9];
if(curLayout.length==0)
{
return [1,2,3,4,5,6,7,8,9];
}
//列排除
for(i=0;i<curLayout.length;i++)
{
line[curLayout[i][index]]=0;
}
//九宮格排除
var col3_3:int = index/3;
var row3_3:int = curLayout.length/3;
var inRow3_3:int = curLayout.length%3;
for(i=row3_3*3;i<row3_3*3+inRow3_3;i++)
{
line[curLayout[i][col3_3*3] ]=0;
line[curLayout[i][col3_3*3+1] ]=0;
line[curLayout[i][col3_3*3+2] ]=0;
}
var ret:Array=[];
for(i=0;i<line.length;i++)
{
if(line[i]!=0)
{
ret.push(i);
}
}
return ret;
}
private function createSudoku():void
{
var arr:Array=createFullSudoku();
var arr2:Array=[];
for(var i:int=0;i<arr.length;i++)
{
arr2.push((arr[i] as Array).join(','));
}
area.text = arr2.join('\n');
}
]]>
</fx:Script>
<s:VGroup horizontalCenter="0" verticalCenter="0">
<s:TextArea width="300" height="300" id="area"/>
<s:Button label="get full sudoku" click="createSudoku()"/>
</s:VGroup>
</s:WindowedApplication>
package model
{
public class DancingNode
{
public var row:int;
public var col:int;
public var rowValue:int;
public var colValue:int;
public var up:DancingNode;
public var down:DancingNode;
public var left:DancingNode;
public var right:DancingNode;
public function DancingNode(r:int=-1,c:int=-1)
{
row = r;
col = c;
up = this;
down = this;
left = this;
right = this;
}
}
}